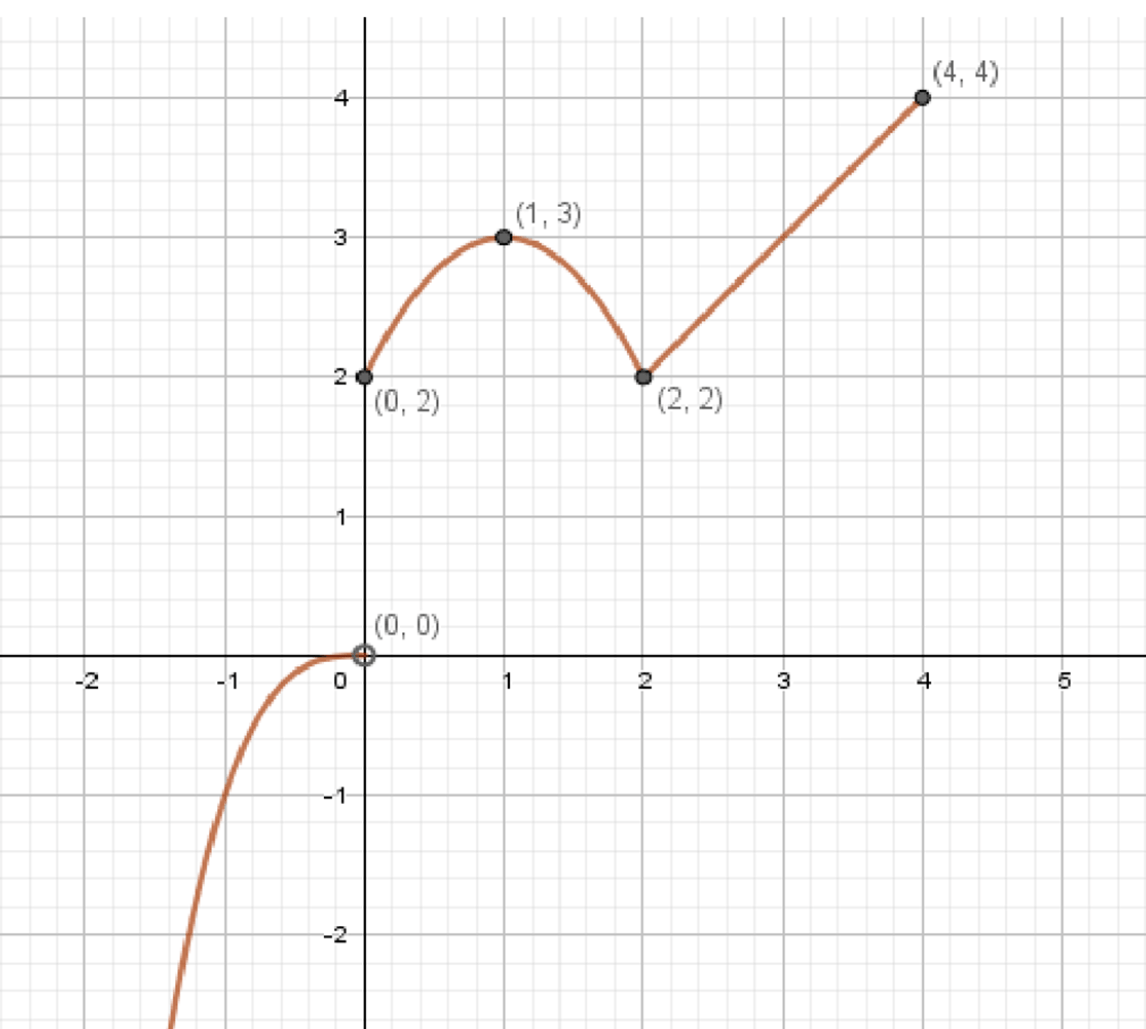ГДЗ 10-11 Класс Номер 2.15 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте и прочитайте график функции:

$$y=\{\begin{array}{ll}{x}^3,& \text{если }x<0;\\ -x^2+2x+2,& \text{если }0\le x\le 2;\\ x,& \text{если }2<x\le 4\end{array}$$

Построить и прочитать график функции:

$$y = \begin{cases} x^3, & \text{если } x < 0; \\ -x^2 + 2x + 2, & \text{если } 0 \leq x \leq 2; \\ x, & \text{если } 2 < x \leq 4 \end{cases}$$

1) $y = x^3$ — кубическая парабола:

$$x_0 = 0, \quad y_0 = 0;$$ $$\begin{array}{|c|c|c|} \hline x & -2 & -1 \\ \hline y & -8 & -1 \\ \hline \end{array}$$

2) $y = -x^2 + 2x + 2$ — уравнение параболы:

$$x_0 = -\frac{b}{2a} = -\frac{2}{2 \cdot (-1)} = \frac{2}{2} = 1;$$ $$y_0 = -1^2 + 2 \cdot 1 + 2 = -1 + 2 + 2 = 3;$$ $$\begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 2 & 2 \\ \hline \end{array}$$

3) $y = x$ — уравнение прямой:

$$\begin{array}{|c|c|c|} \hline x & 2 & 4 \\ \hline y & 2 & 4 \\ \hline \end{array}$$

4) График функции:

5) Свойства функции:

$$D(y) = (-\infty; 4], \quad E(y) = (-\infty; 0) \cup [2; 4];$$

• Возрастает на $(-\infty; 0) \cup [0; 1] \cup [2; 4]$;
• Убывает на $[1; 2]$;
• Не ограничена снизу, ограничена сверху;
• $y_{\text{наиб}} = y(4) = 4$, $y_{\text{наим}}$ — не существует;
• Функция непрерывна на $(-\infty; 0) \cup (0; 4)$.

Рассмотрим функцию:

$$y = \begin{cases} x^3, & \text{если } x < 0; \\ -x^2 + 2x + 2, & \text{если } 0 \leq x \leq 2; \\ x, & \text{если } 2 < x \leq 4 \end{cases}$$

Функция состоит из трех частей, каждая из которых имеет свою формулу, и необходимо построить график для разных интервалов.

1) График функции $y = x^3$ для $x < 0$

Это кубическая функция, и её график — кубическая парабола. Рассмотрим несколько значений $x$, чтобы увидеть, как ведет себя функция:

• Когда $x = -2$:

  $$y = (-2)^3 = -8$$

• Когда $x = -1$:

  $$y = (-1)^3 = -1$$

• Когда $x = 0$:

  $$y = 0^3 = 0$$

Таким образом, для $x < 0$ график будет изгибаться вниз, проходя через точку $(0, 0)$.

Таблица значений:

$$\begin{array}{|c|c|c|} \hline x & -2 & -1 \\ \hline y & -8 & -1 \\ \hline \end{array}$$

2) График функции $y = -x^2 + 2x + 2$ для $0 \leq x \leq 2$

Это квадратичная функция (парабола), и её график будет иметь форму параболы, открывающейся вниз, так как коэффициент при $x^2$ отрицательный.

Чтобы построить график, найдем вершину параболы. Для этого используем формулу для абсциссы вершины $x_0$ параболы:

$$x_0 = -\frac{b}{2a}$$

где $a = -1$, $b = 2$, и $c = 2$ — коэффициенты квадратного уравнения.

Вычислим $x_0$:

$$x_0 = -\frac{2}{2 \cdot (-1)} = \frac{2}{2} = 1$$

Теперь находим значение функции в вершине, подставив $x = 1$ в уравнение:

$$y_0 = -1^2 + 2 \cdot 1 + 2 = -1 + 2 + 2 = 3$$

Таким образом, вершина параболы находится в точке $(1, 3)$.

Теперь определим значения функции в других точках интервала $0 \leq x \leq 2$:

• Когда $x = 0$:

  $$y = -0^2 + 2 \cdot 0 + 2 = 2$$

• Когда $x = 2$:

  $$y = -(2)^2 + 2 \cdot 2 + 2 = -4 + 4 + 2 = 2$$

Таблица значений:

$$\begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 2 & 2 \\ \hline \end{array}$$

3) График функции $y = x$ для $2 < x \leq 4$

Это линейная функция с угловым коэффициентом 1. График этой функции представляет собой прямую линию, проходящую через начало координат с угловым коэффициентом 1.

Для построения графика определим значения функции в точках:

• Когда $x = 2$:

  $$y = 2$$

• Когда $x = 4$:

  $$y = 4$$

Таблица значений:

$$\begin{array}{|c|c|c|} \hline x & 2 & 4 \\ \hline y & 2 & 4 \\ \hline \end{array}$$

4) График функции

График функции $y$ представляет собой комбинацию из трех частей:

1. Для $x < 0$ — кубическая функция $y = x^3$, график которой проходит через начало координат и убывает влево.
2. Для $0 \leq x \leq 2$ — парабола, открывающаяся вниз, с вершиной в точке $(1, 3)$, проходящая через точки $(0, 2)$ и $(2, 2)$.
3. Для $2 < x \leq 4$ — прямая $y = x$, которая проходит через точки $(2, 2)$ и $(4, 4)$.

5) Свойства функции

Область определения (D)

Область определения функции $D(y)$ — это множество всех значений $x$, для которых функция определена. Поскольку функция представлена на интервалах $(-\infty; 0)$, $[0; 2]$, и $(2; 4]$, то область определения функции:

$$D(y) = (-\infty; 4]$$

Область значений (E)

Область значений функции $E(y)$ — это множество всех возможных значений $y$, которые может принимать функция. Для каждого из интервалов $x$ мы рассмотрим значения функции:

• Для $x < 0$ функция $y = x^3$ принимает значения от $-\infty$ до 0.
• Для $0 \leq x \leq 2$ функция $y = -x^2 + 2x + 2$ принимает значения от 2 до 3.
• Для $2 < x \leq 4$ функция $y = x$ принимает значения от 2 до 4.

Таким образом, область значений функции:

$$E(y) = (-\infty; 0) \cup [2; 4]$$

Монотонность функции

• Функция возрастает на интервалах:

  $$(-\infty; 0), \quad [0; 1], \quad [2; 4]$$

• Функция убывает на интервале:

  $$[1; 2]$$

Ограниченность функции

• Функция не ограничена снизу (так как $y = x^3$ для $x \to -\infty$ уходит в минус).
• Функция ограничена сверху, так как её максимальное значение достигается в точке $(4, 4)$, и $y_{\text{max}} = 4$.

Экстремумы функции

• Наибольшее значение функции $y_{\text{max}} = 4$ достигается в точке $x = 4$.
• Наименьшее значение функции не существует, так как $y \to -\infty$ при $x \to -\infty$.

Непрерывность функции

Функция непрерывна на интервалах:

$$(-\infty; 0), \quad (0; 4)$$

но не непрерывна в точке $x = 0$ и $x = 2$, так как на этих точках происходит изменение формы графика (из кубической функции в параболу и из параболы в прямую).