ГДЗ 10-11 Класс Номер 22.36 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а)

$$y = \sqrt{2}(\sin x + \cos x) = \sqrt{2} \sin x + \sqrt{2} \cos x;$$ $$$$б)

$$y = \sqrt{3} \sin x + \cos x;$$ $$$$в)

$$y = \sin x — \sqrt{3} \cos x;$$ $$$$г)

$$y=\sin x-\cos x$$

Построить график функции:

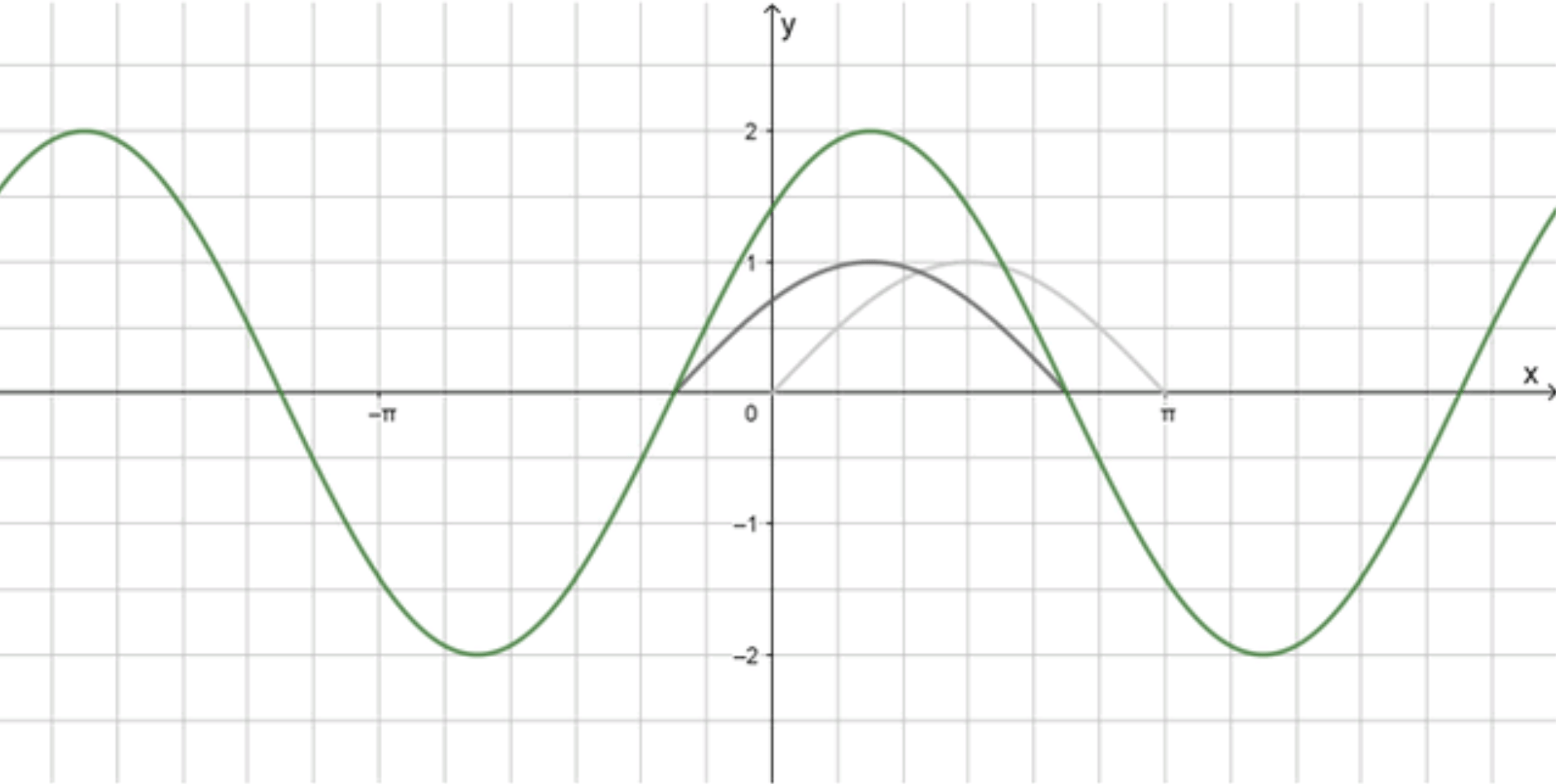
а)

$$y = \sqrt{2}(\sin x + \cos x) = \sqrt{2} \sin x + \sqrt{2} \cos x;$$ $$y = 2\left( \frac{\sqrt{2}}{2} \sin x + \frac{\sqrt{2}}{2} \cos x \right) = 2 \sin(x + t) = 2 \sin\left(x + \frac{\pi}{4}\right);$$ $$C = \sqrt{2} + 2 = \sqrt{4} = 2;$$ $$\cos t = \frac{\sqrt{2}}{2};$$ $$t = \arccos \frac{\sqrt{2}}{2} = \frac{\pi}{4};$$

График функции

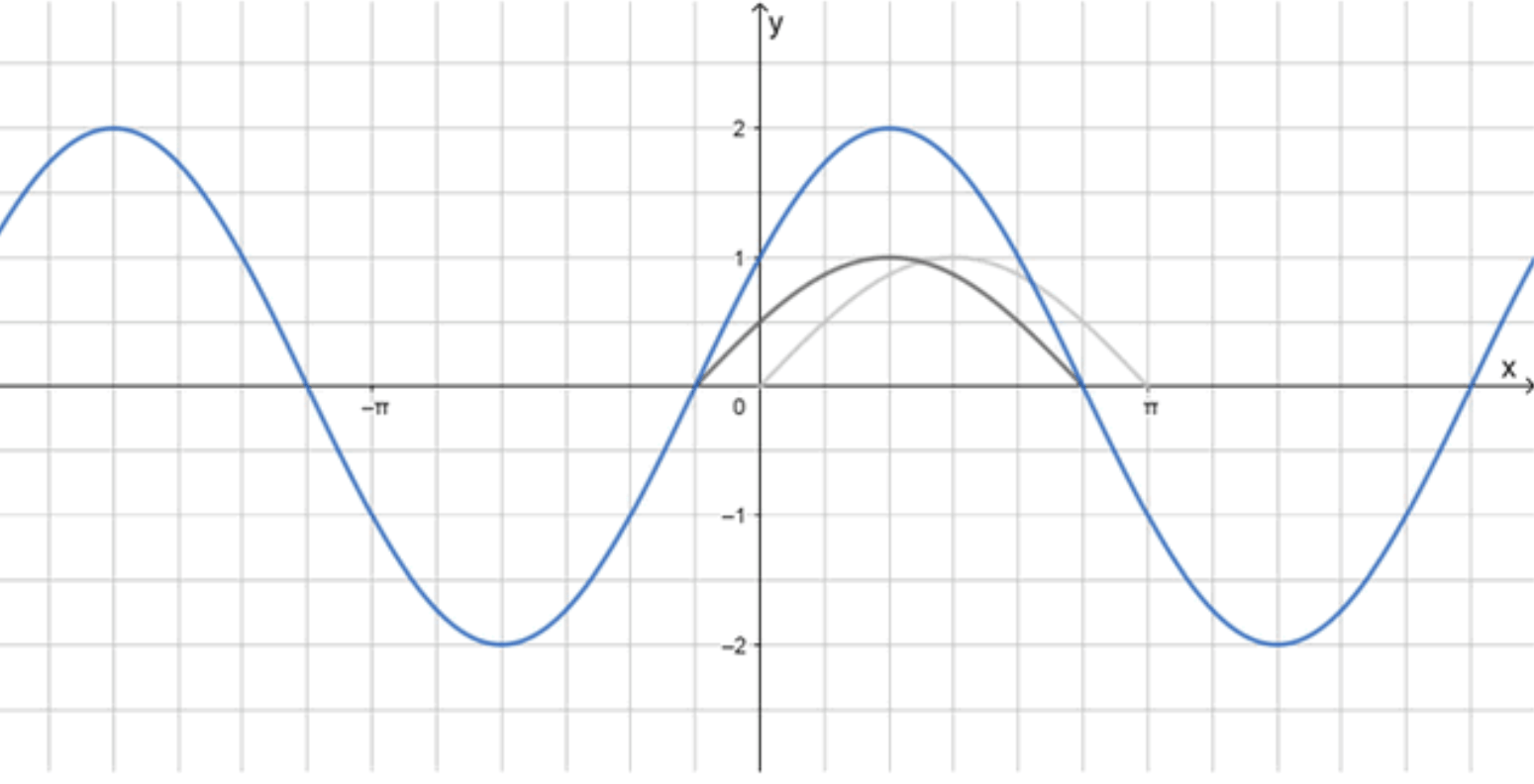
б)

$$y = \sqrt{3} \sin x + \cos x;$$ $$y = 2\left( \frac{\sqrt{3}}{2} \sin x + \frac{1}{2} \cos x \right) = 2 \sin(x + t) = 2 \sin\left(x + \frac{\pi}{6}\right);$$ $$C = \sqrt{3} + 1 = \sqrt{4} = 2;$$ $$\cos t = \frac{\sqrt{3}}{2};$$ $$t = \arccos \frac{\sqrt{3}}{2} = \frac{\pi}{6};$$

График функции

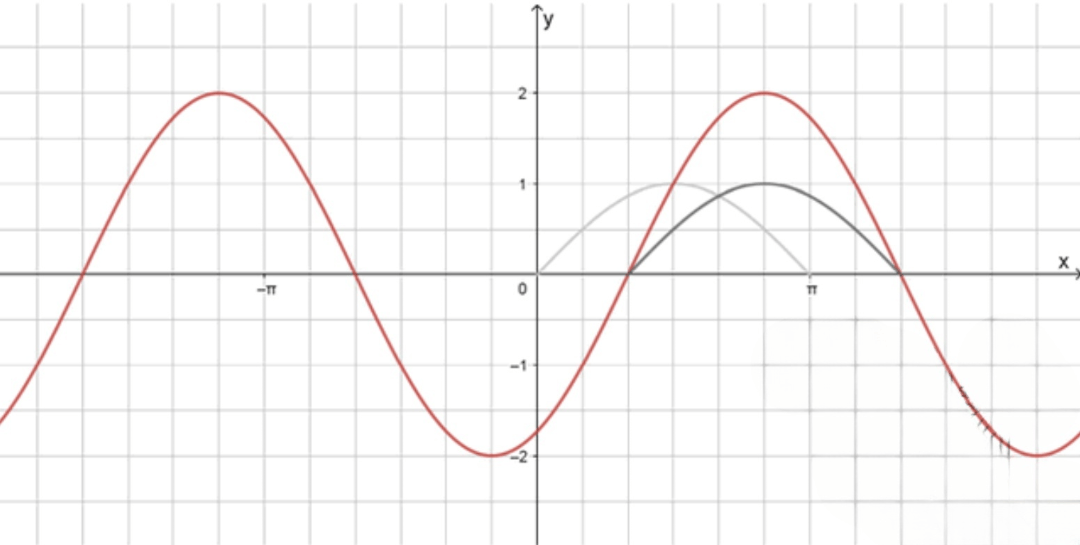
в)

$$y = \sin x — \sqrt{3} \cos x;$$ $$y = 2\left( \frac{1}{2} \sin x — \frac{\sqrt{3}}{2} \cos x \right) = 2 \sin(x — t) = 2 \sin\left(x — \frac{\pi}{3}\right);$$ $$C = \sqrt{1 + 3} = \sqrt{4} = 2;$$ $$\cos t = \frac{1}{2};$$ $$t = \arccos \frac{1}{2} = \frac{\pi}{3};$$

График функции

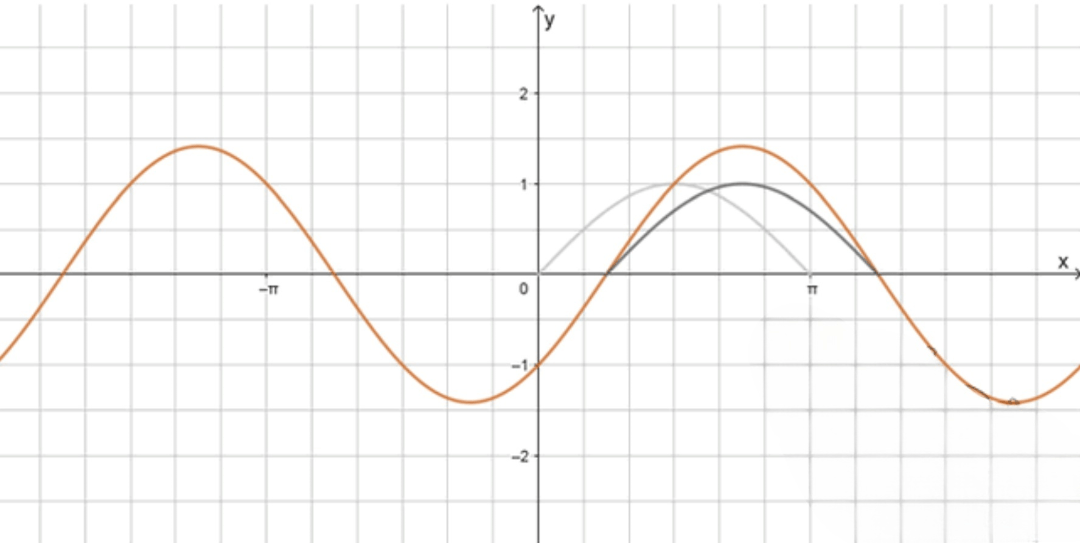
г)

$$y = \sin x — \cos x;$$ $$y = \sqrt{2}\left( \frac{\sqrt{2}}{2} \sin x — \frac{\sqrt{2}}{2} \cos x \right) = \sqrt{2} \sin(x — t) = \sqrt{2} \sin\left(x — \frac{\pi}{4}\right);$$ $$C = \sqrt{1 + 1} = \sqrt{2};$$ $$\cos t = \frac{\sqrt{2}}{2};$$ $$t = \arccos \frac{\sqrt{2}}{2} = \frac{\pi}{4};$$

График функции

Как строить график функции $y = C \sin(x + t)$

Функция:

$$y = C \sin(x + t)$$

представляет собой синусоиду с:

• амплитудой $C$ — максимальное значение по оси $y$,
• периодом $T = 2\pi$,
• фазовым сдвигом: $+t$ сдвигает график влево, $-t$ — вправо,
• осевой линией (середина между максимумом и минимумом): здесь — $y = 0$, так как нет вертикального сдвига.

а) $y = \sqrt{2} (\sin x + \cos x)$

Преобразование:

$$y = \sqrt{2} \sin x + \sqrt{2} \cos x = 2 \sin\left(x + \frac{\pi}{4}\right)$$

Характеристики графика:

• Амплитуда: 2
• Период: $2\pi$
• Фаза (сдвиг): $+\frac{\pi}{4}$ → график сдвинут влево
• Максимум: $y = 2$, минимум: $y = -2$

Как построить:

1. Начинай с обычного графика $y = \sin x$.
2. Увеличь амплитуду до 2.
3. Сдвинь весь график на $\frac{\pi}{4}$ влево.
4. Отметь ключевые точки:
   • Начало: $x = -\frac{\pi}{4}$, $y = 0$
   • Пик: $x = \frac{\pi}{4}$, $y = 2$
   • Ноль: $x = \frac{3\pi}{4}$, $y = 0$
   • Минимум: $x = \frac{5\pi}{4}$, $y = -2$
   • Возврат к нулю: $x = \frac{7\pi}{4}$, $y = 0$

б) $y = \sqrt{3} \sin x + \cos x$

Преобразование:

$$y = 2 \sin\left(x + \frac{\pi}{6}\right)$$

Характеристики графика:

• Амплитуда: 2
• Период: $2\pi$
• Сдвиг: $+\frac{\pi}{6}$ (влево)
• Максимум/минимум: 2 и -2

Построение:

1. Строй график $y = \sin x$, затем умножь амплитуду на 2.
2. Сдвинь график влево на $\frac{\pi}{6}$.
3. Основные точки:
   • Ноль: $x = -\frac{\pi}{6}$
   • Пик: $x = \frac{\pi}{6}$
   • Следующий ноль: $x = \frac{5\pi}{6}$
   • Минимум: $x = \frac{7\pi}{6}$

в) $y = \sin x — \sqrt{3} \cos x$

Преобразование:

$$y = 2 \sin\left(x — \frac{\pi}{3}\right)$$

Характеристики:

• Амплитуда: 2
• Период: $2\pi$
• Сдвиг: $-\frac{\pi}{3}$ (вправо)

Построение:

1. Начинай с $y = 2 \sin x$.
2. Сдвинь вправо на $\frac{\pi}{3}$.
3. Ключевые точки:
   • Ноль: $x = \frac{\pi}{3}$
   • Пик: $x = \frac{5\pi}{6}$
   • Ноль: $x = \frac{7\pi}{6}$
   • Минимум: $x = \frac{11\pi}{6}$

г) $y = \sin x — \cos x$

Преобразование:

$$y = \sqrt{2} \sin\left(x — \frac{\pi}{4}\right)$$

Характеристики:

• Амплитуда: $\sqrt{2} \approx 1.41$
• Период: $2\pi$
• Сдвиг: вправо на $\frac{\pi}{4}$

Построение:

1. Строй график $y = \sin x$, амплитуда теперь $\sqrt{2}$
2. Сдвинь вправо на $\frac{\pi}{4}$
3. Отметь:
   • Ноль: $x = \frac{\pi}{4}$
   • Пик: $x = \frac{3\pi}{4}$
   • Следующий ноль: $x = \frac{5\pi}{4}$
   • Минимум: $x=\frac{7\pi }{4}$