ГДЗ 10-11 Класс Номер 26.10 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

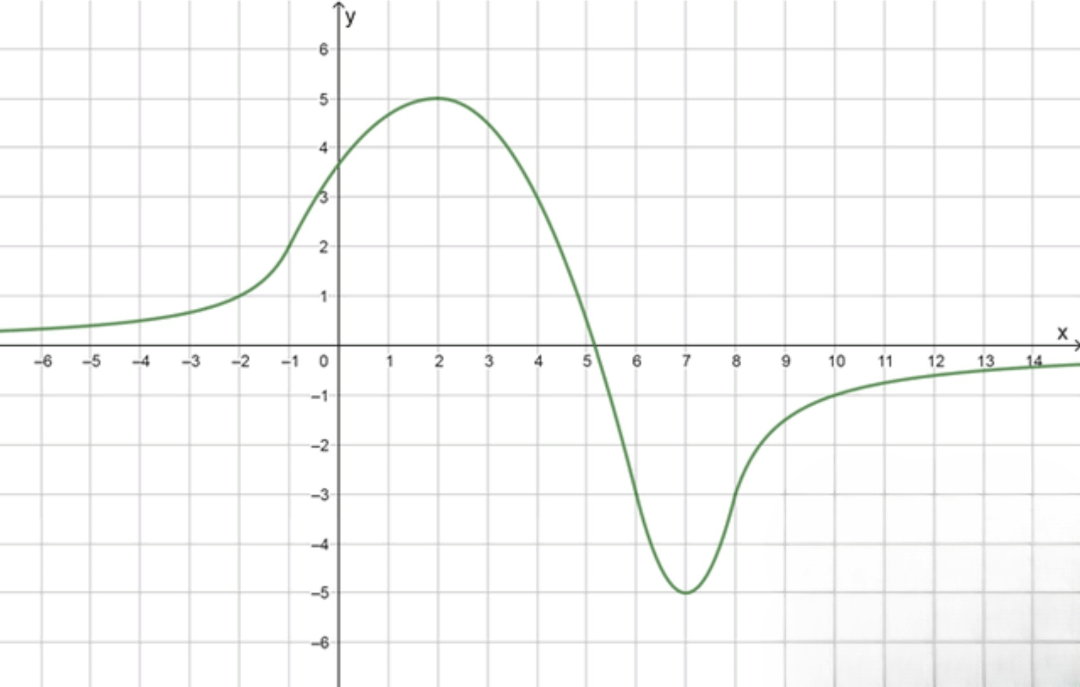
Изобразите график непрерывной на $(-\infty; +\infty)$ функции у = f(x), обладающей следующими свойствами:

$\lim_{x \to -\infty} f(x) = 0$; $f(x) > 0$ на $(-\infty; 0)$; $E(f) = [-5; 5]$; Функция убывает на $[2; 7]$.

Изобразить график непрерывной на $(-\infty; +\infty)$ функции $y = f(x)$;

Свойства функции:

• $\lim_{x \to -\infty} f(x) = 0$;
• $f(x) > 0$ на $(-\infty; 0)$;
• $E(f) = [-5; 5]$;
• Функция убывает на $[2; 7]$;

График функции:

Необходимо изобразить график функции $y = f(x)$, непрерывной на $(-\infty, +\infty)$, с такими свойствами:

1. $\lim_{x \to -\infty} f(x) = 0$ — при $x \to -\infty$ функция стремится к 0.
2. $f(x) > 0$ на $(-\infty, 0)$ — до включительно нуля функция положительна.
3. $E(f) = [-5; 5]$ — область значений функции, или её range, это от $-5$ до $+5$ включительно.
4. Функция убывает на интервале $[2; 7]$.

Подход к построению графика

1. Основа: асимптотическое поведение при $x \to -\infty$

• Нарисуй ось $x$ и $y$.
• Отметь горизонтальную линию $y = 0$ (возможно пунктиром) как асимптоту слева.
• Кривая должна приближаться к этой линии, но оставаться выше (так как $f(x) > 0$ на $(-\infty, 0)$).

2. Ограниченность значений $[-5; 5]$

• Отметь горизонтальные линии $y = 5$ и $y = -5$.
• График не должен выходить выше $y = 5$ и ниже $y = -5$.
• Значения должны заполнять этот диапазон, т.е. на нём функция могут достигать граничных значений.

3. Поведение на $(-\infty, 0)$

• Слева (при больших отрицательных $x$) функция стремится к 0 сверху.
• Находится выше оси $y = 0$, но не пересекает её.
• Далее (подходя к $x = 0$) функция может либо увеличиться, либо уменьшиться, но остаётся положительной.

4. Общая непрерывность и диапазон значений

• Должна быть непрерывной — без скачков, разрывов, вертикальных асимптот.
• Значения от $0$ до $5$ (и возможно до $-5$ как минимум), то есть график должен спускаться до отрицательных значений после $x>0$, чтобы достичь $-5$.

5. Убывание на $[2; 7]$

• На отрезке $x \in [2; 7]$ функция строго убывает.
• В этот отрезок входят как падающие визуально точки.
• Значение в начале (в точке $x = 2$) должно быть выше, а к $x = 7$ быть ниже.

Пример функции и ее графика

Выбор функции

Возьмём кусочную конструкцию:

$$f(x) = \begin{cases} \dfrac{1}{|x| + 1}, & x \leq 0, \\ 5 \cdot \dfrac{ (7 — x) }{7 — 2}, & x \in [2,7], \\ \dots \end{cases}$$

Объяснение:

• При $x \to -\infty$, $\frac{1}{|x| + 1} \to 0$. При этом $> 0$ для $x<0$.
• Легко масштабировать, чтобы значения находятся в $[-5,5]$.
• На $[2,7]$ берём линейный спад от $5$ до $-5$, строго убывающий.

Добавим переход между 0 и 2 небольшим сглаживанием, оставляя непрерывность.

Как построить эскиз

1. Асимптота слева: при $x \to -\infty$ функция поднимается к 0, не пересекает ось.
2. Положительный участок до $x = 0$: плавный подъём или спад в районе $(-\infty, 0)$, не покидая диапазон $(0,5]$.
3. Переход от $0$ до $2$: постепенно внутрь диапазона, непрерывно соединяем с убывающей частью.
4. Uбывающий участок $[2,7]$: график спускается линейно или гладко от $5$ до $-5$.
5. После $x = 7$: продолжаем плавно в пределах $[-5,5]$, например, горизонтальный участок при $y = -5$.

Визуальное описание

• Слева — кривая, которая начинается выше оси $y=0$, стремится к ней при $x \to -\infty$.
• Далее — плавный график достигает максимум около $y = 5$, затем спуск к $y = -5$ на участке [2,7].
• После $x=7$ — функцию можно сделать горизонтальной (постоянной $-5$).