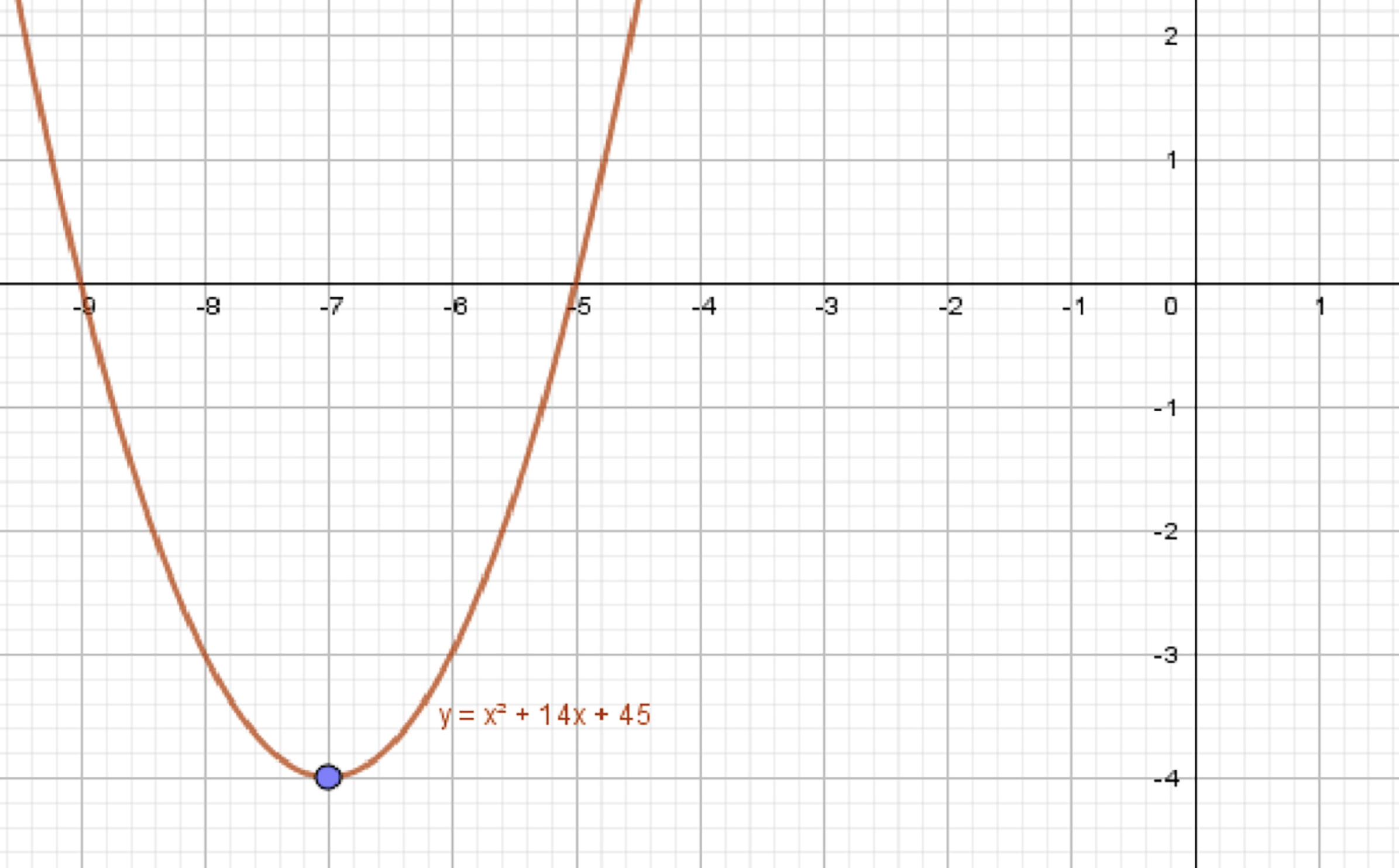ГДЗ 10-11 Класс Номер 26.17 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Изобразите эскиз графика какой-нибудь функции y = g(x), обладающей заданным свойством:

а) $\lim_{x \to -1} g(x) = 2$;

б) $\lim_{x \to 2} g(x) = -3$;

в) $\lim_{x \to -7} g(x) = -4$;

г) $\lim_{x \to 5} g(x) = 3{,}5$

Построить эскиз графика какой-нибудь функции $y = g(x)$, обладающей указанным свойством:

а) $\lim_{x \to -1} g(x) = 2$;

б) $\lim_{x \to 2} g(x) = -3$;

в) $\lim_{x \to -7} g(x) = -4$;

г) $\lim_{x \to 5} g(x) = 3{,}5$;

Теория: Что значит $\lim_{x \to a} g(x) = L$

Это означает следующее:

При приближении $x$ к числу $a$ (как слева, так и справа), значения функции $g(x)$ стремятся к числу $L$.

Важно:
Это НЕ требует, чтобы:

• функция была определена в точке $a$;
• $g(a) = L$.

Цель: Построить эскиз функции $g(x)$, обладающей заданным пределом.

Эскиз — это приближённый, схематический график, показывающий поведение функции около интересующей нас точки.

Для каждого случая будем:

1. Выбирать простую форму графика (например, прямую или сглаженную кривую).
2. Указывать поведение функции вокруг заданной точки.
3. При желании, можно нарисовать «дырку» в точке $x = a$ (если хотим, чтобы функция была неопределена в точке, но предел существовал).

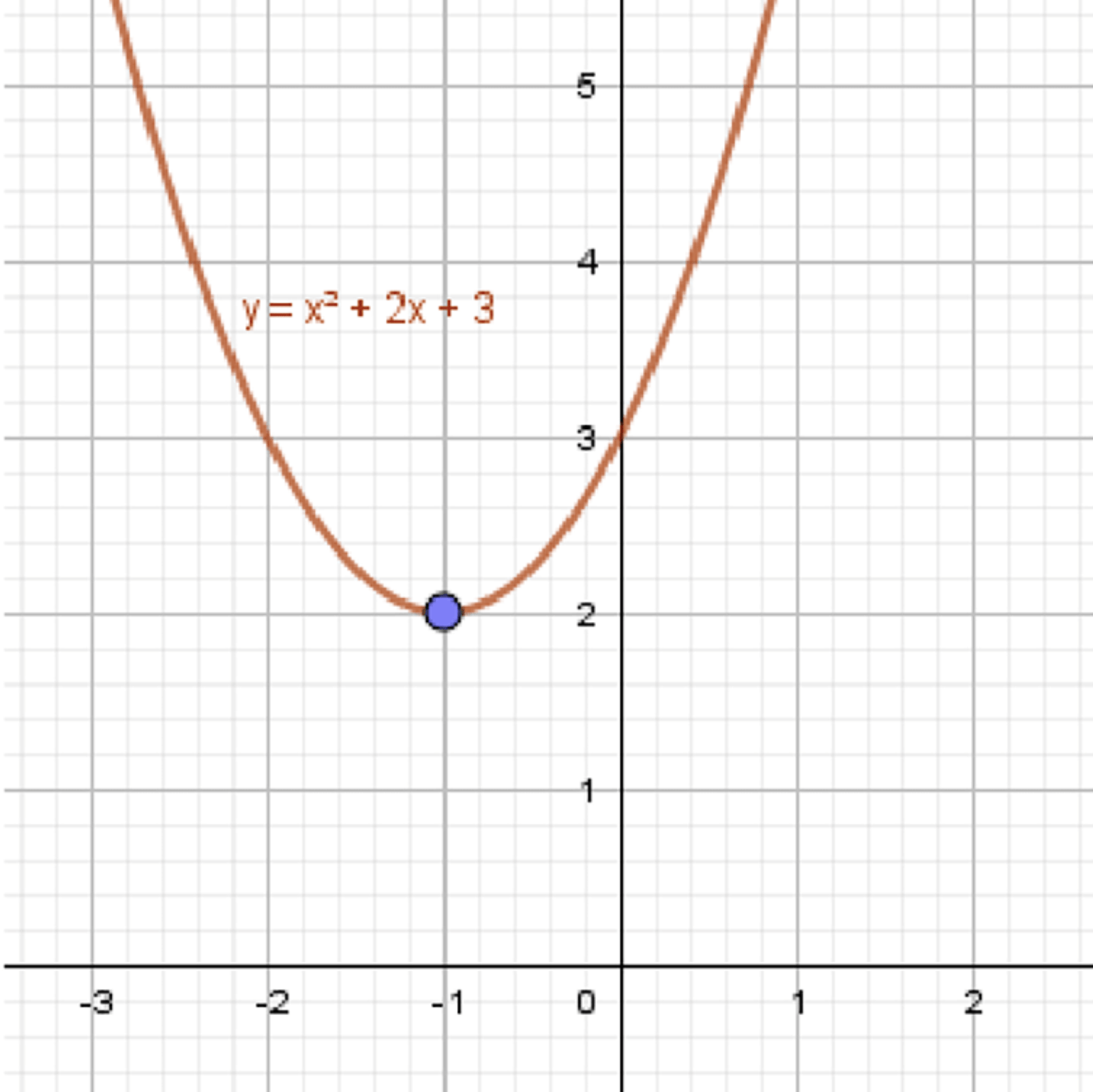
а) $\lim_{x \to -1} g(x) = 2$

Что это значит:

Когда $x \to -1$, значения функции $g(x) \to 2$.

Как должен выглядеть график:

• Возле точки $x = -1$, график плавно приближается к уровню $y = 2$.
• Можно нарисовать гладкую кривую, проходящую вблизи точки $(-1, 2)$.
• В точке $x = -1$ может быть:
  • либо точка $(-1, 2)$,
  • либо пустое место (дырка) — не влияет на предел.

Пример:

Пусть:

$$g(x) = 2 + (x + 1)\sin\left(\frac{1}{x + 1}\right), \quad x \ne -1$$

Это функция, колеблющаяся, но стремящаяся к 2 при $x \to -1$.

Как построить:

Провести горизонтальную пунктирную линию $y = 2$.

Вблизи $x = -1$, нарисовать кривую, приближающуюся к $y = 2$.

В точке $x = -1$:

• можно оставить «дырку»;
• или поставить точку в $(-1, 2)$.

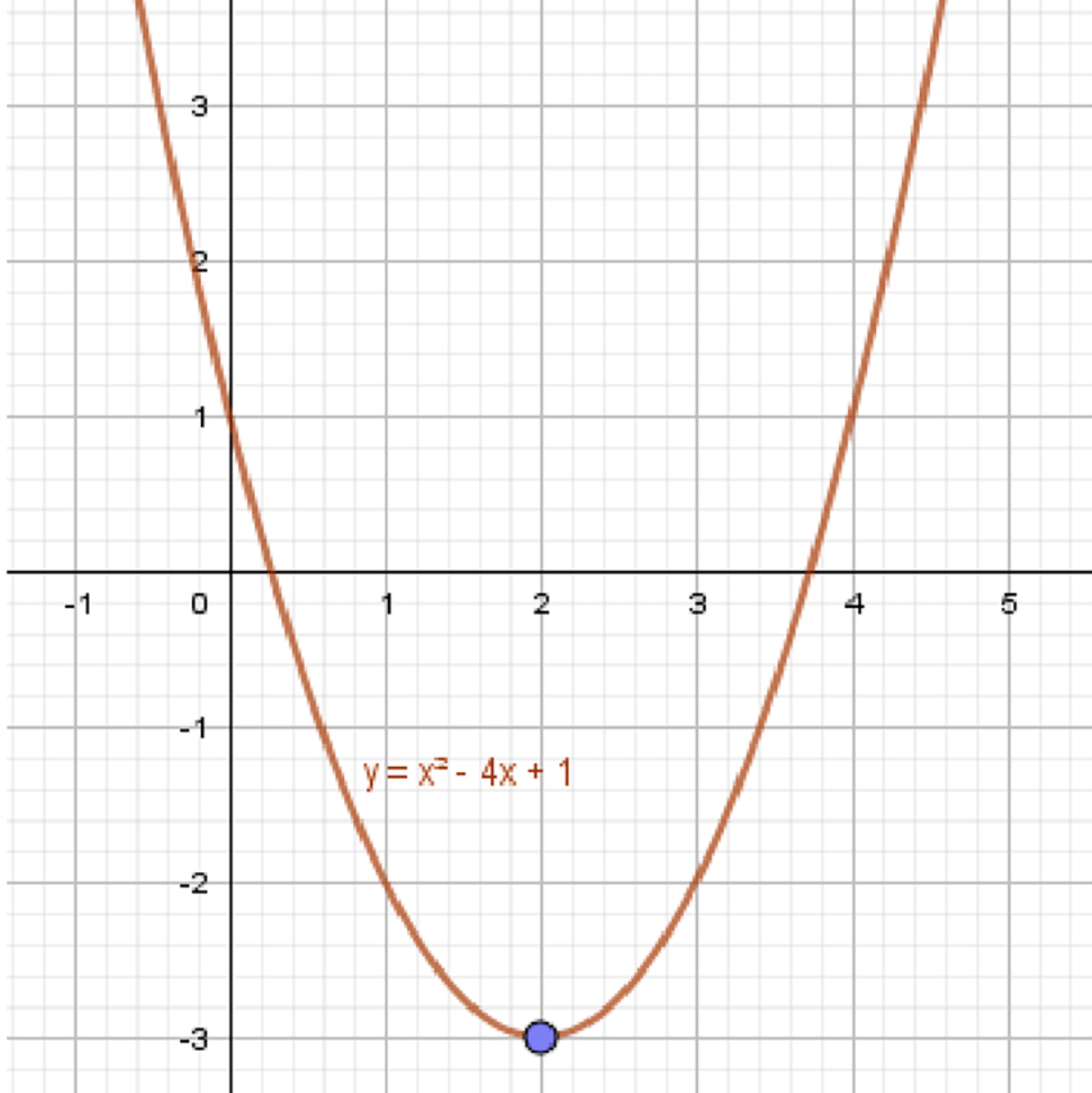
б) $\lim_{x \to 2} g(x) = -3$

Что это значит:

При приближении к $x = 2$, функция стремится к $-3$.

Вид графика:

• Вблизи точки $x = 2$, график плавно подходит к уровню $y = -3$.
• Поведение функции слева и справа от $x = 2$ одинаково.

Пример:

Пусть:

$$g(x) = -3 + \frac{x — 2}{x^2 + 1}$$

При $x \to 2$, дробь $\frac{x — 2}{x^2 + 1} \to 0$, значит $g(x) \to -3$.

Как построить:

1. Нарисовать горизонтальную пунктирную линию $y = -3$.
2. Вблизи $x = 2$, нарисовать кривую, стремящуюся к этой линии.
3. В точке $x = 2$ — можно оставить «дырку» или поставить точку.

в) $\lim_{x \to -7} g(x) = -4$

Значение:

Функция $g(x)$ стремится к $-4$ при $x \to -7$.

Вид графика:

• График приближается к уровню $y = -4$ слева и справа от $x = -7$.

Пример:

Пусть:

$$g(x) = -4 + \frac{\sin(x + 7)}{x + 7}, \quad x \ne -7$$

Функция стремится к -4, но может иметь разрыв в точке.

Построение:

1. Провести пунктир $y = -4$.
2. Нарисовать поведение кривой около $x = -7$.
3. Оставить точку открытой или закрытой в $x = -7$.

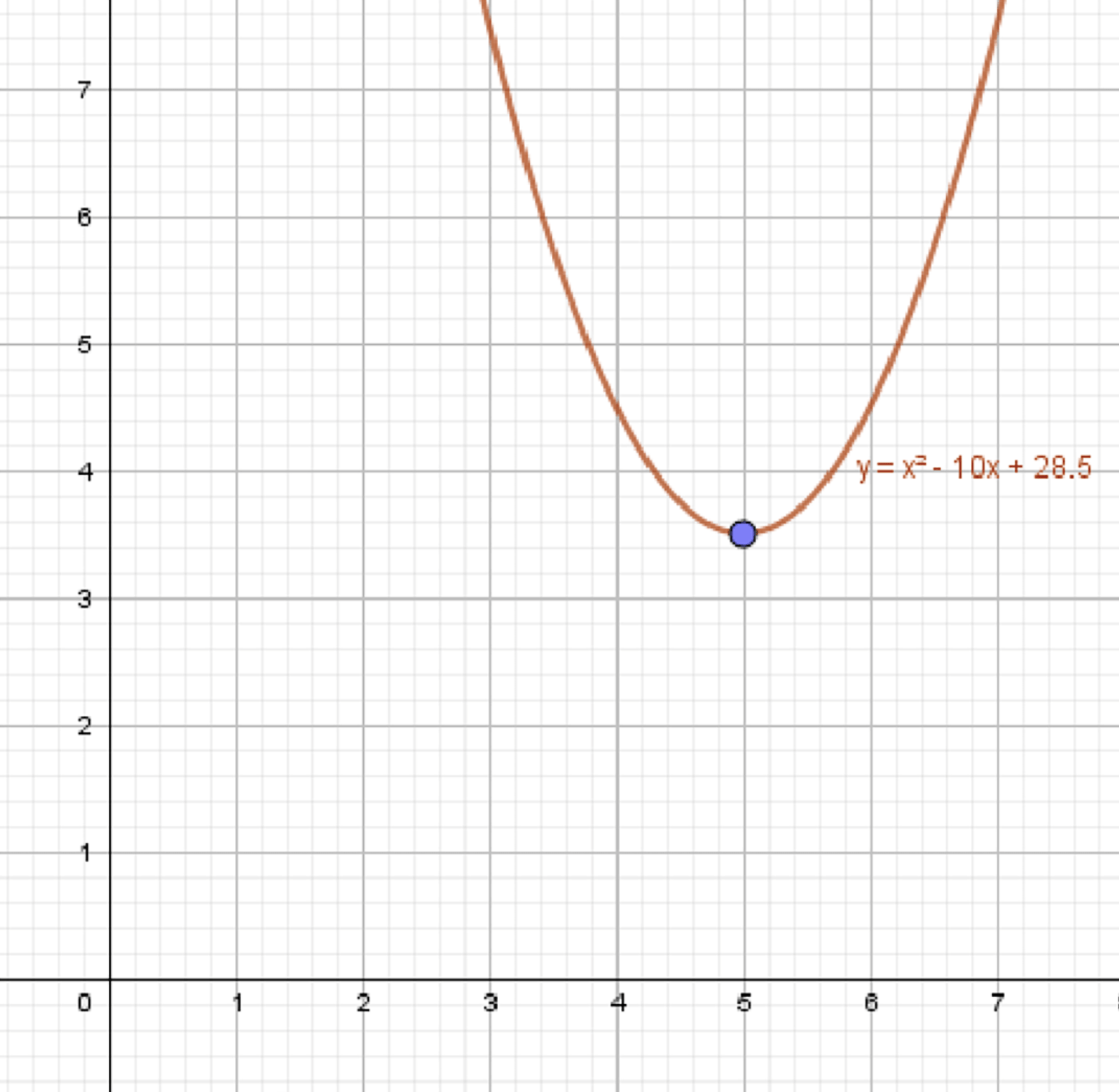
г) $\lim_{x \to 5} g(x) = 3{,}5$

Значение:

При приближении к $x = 5$, значения $g(x) \to 3.5$.

Вид графика:

• График идёт к уровню $y = 3.5$.
• Можно нарисовать плавную линию, например, отрезок, приближающийся к этому значению.

Пример:

Пусть:

$$g(x) = 3.5 + (x — 5)^2 \cdot \sin\left(\frac{1}{x — 5}\right), \quad x \ne 5$$

Функция колеблется, но стремится к 3.5 при $x \to 5$.

Построение:

1. Нарисовать горизонтальную линию $y = 3.5$.
2. Изобразить плавное приближение к этой линии около $x = 5$.
3. В самой точке — можно не ставить точку.