Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 26.19 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Постройте эскиз графика какой-нибудь функции y = f(x), обладающей заданными свойствами:
а) и ;
б) и ;
в) и не существует;
г) и
Построить эскиз графика какой-нибудь функции , обладающей указанными свойствами:
а) и ;
б) и ;
в) и не существует;
г) и
Чтобы понять, как должен выглядеть график, нужно различать два понятия:
Предел
Это значит:
Когда приближается к (слева и справа), значения функции стремятся к , независимо от того, существует ли сама точка .
Значение функции
Это просто точка на графике в координатах , если она определена.
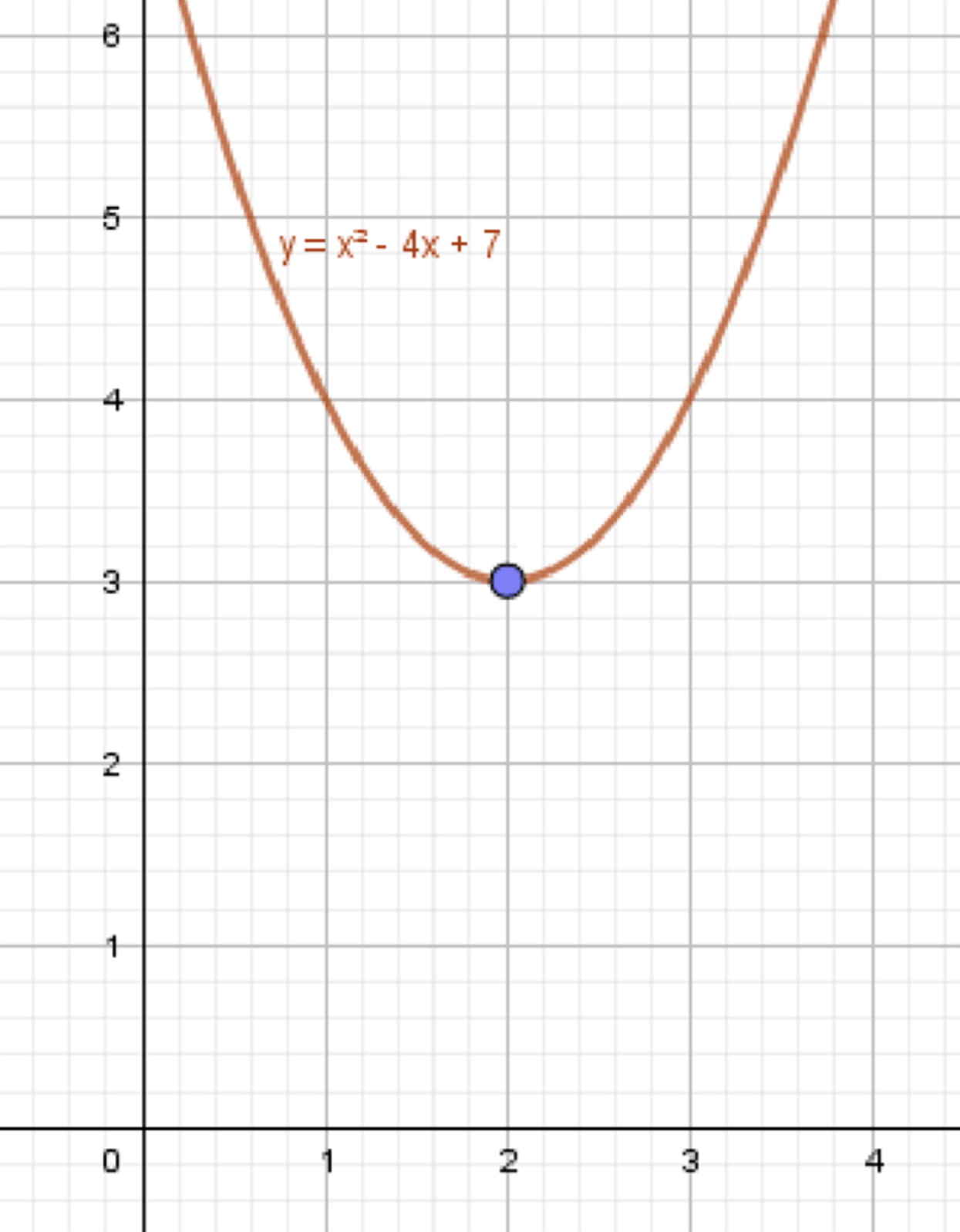
а) и
Что это значит:
- График плавно приближается к точке с обеих сторон.
- Функция определена в точке , и значение функции совпадает с пределом.
Это случай непрерывности в точке .
Как выглядит график:
- Обычная гладкая линия (например, отрезок прямой), без разрывов.
- В точке график проходит через точку без скачков.
Как построить:
- Нарисуйте оси координат.
- Отметьте точку .
- Проведите плавную линию, подходящую к этой точке слева и справа (например, прямую возле 2).
- Подчеркните, что в самой точке график есть, без «дырки».
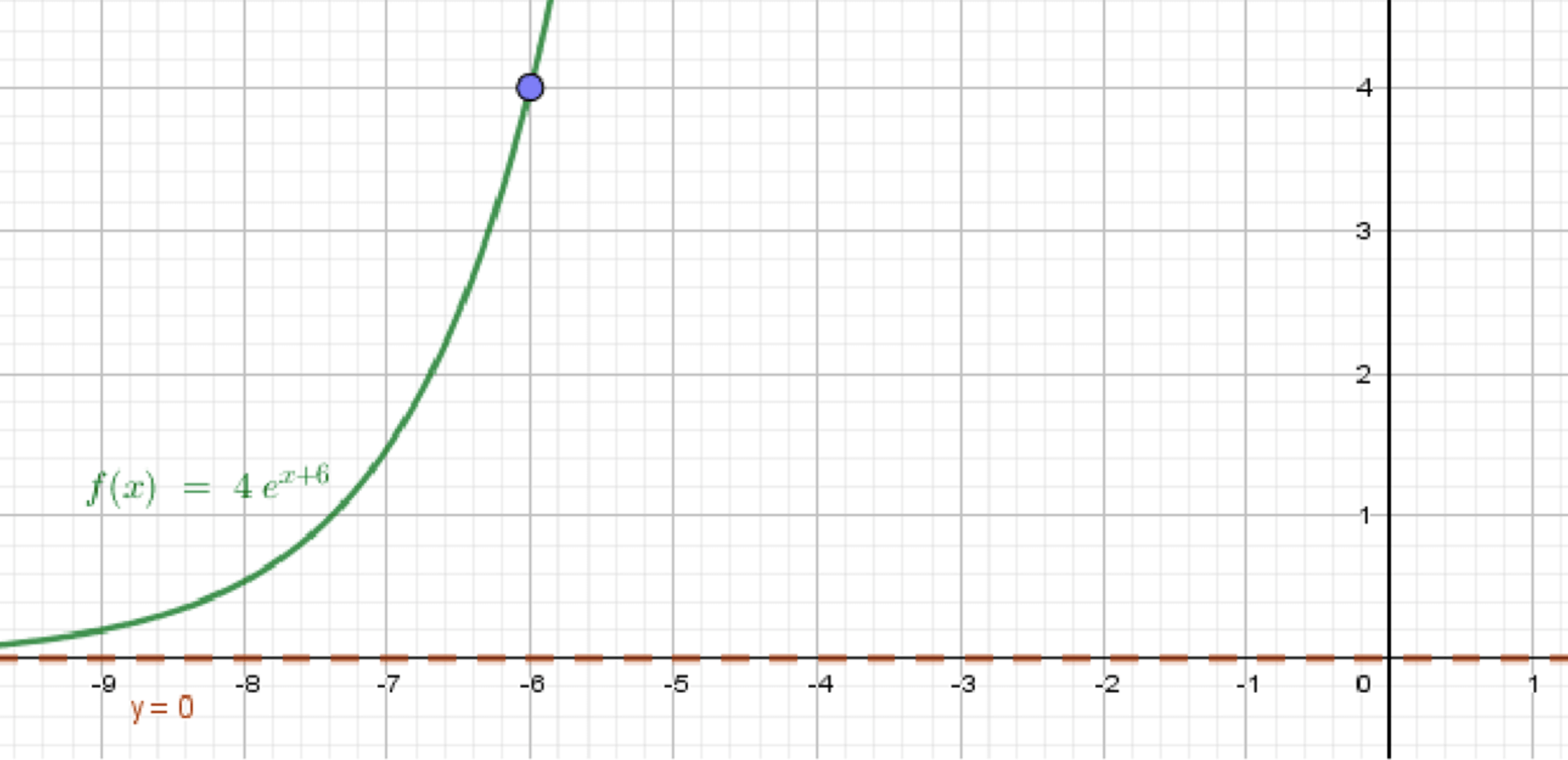
б) и
Что это значит:
- При , график подходит к значению .
- При , график стремится к 0, т.е. приближается к горизонтальной асимптоте .
Как выглядит график:
- Слева далеко (очень большие отрицательные ) график почти «лежит» на .
- Приближаясь к , график плавно поднимается к .
- Точка может существовать или не существовать — не важно для предела.
Как построить:
- Проведите горизонтальную пунктирную линию — асимптота.
- Нарисуйте график, начинающийся далеко слева чуть выше нуля.
- Пусть кривая плавно поднимается вверх к точке , приближаясь к значению .
- Можно поставить точку в , если хотите, или оставить «дырку».
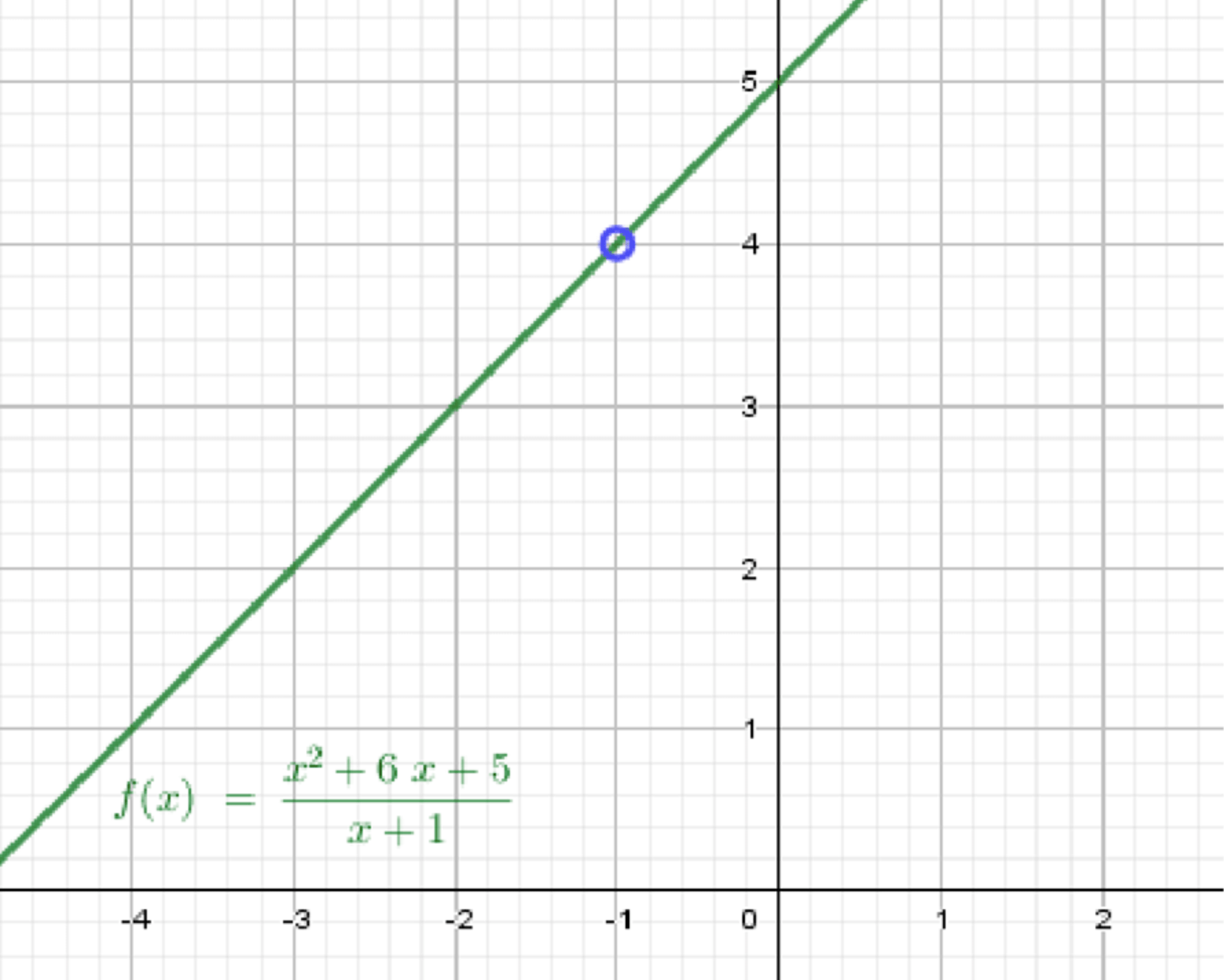
в) и не существует
Что это значит:
- При приближении к с обеих сторон, график стремится к .
- Но в самой точке нет значения функции — то есть, либо «дырка», либо вообще не определено.
Как выглядит график:
- Слева и справа от график тянется к уровню .
- В самой точке — «пробел», т.е. функция не имеет значения.
Как построить:
- Нарисуйте оси координат.
- Отметьте точку .
- Проведите кривую, подходящую к уровню слева и справа от .
- В самой точке нарисуйте дырку (пустой кружок) на уровне или ничего не ставьте.
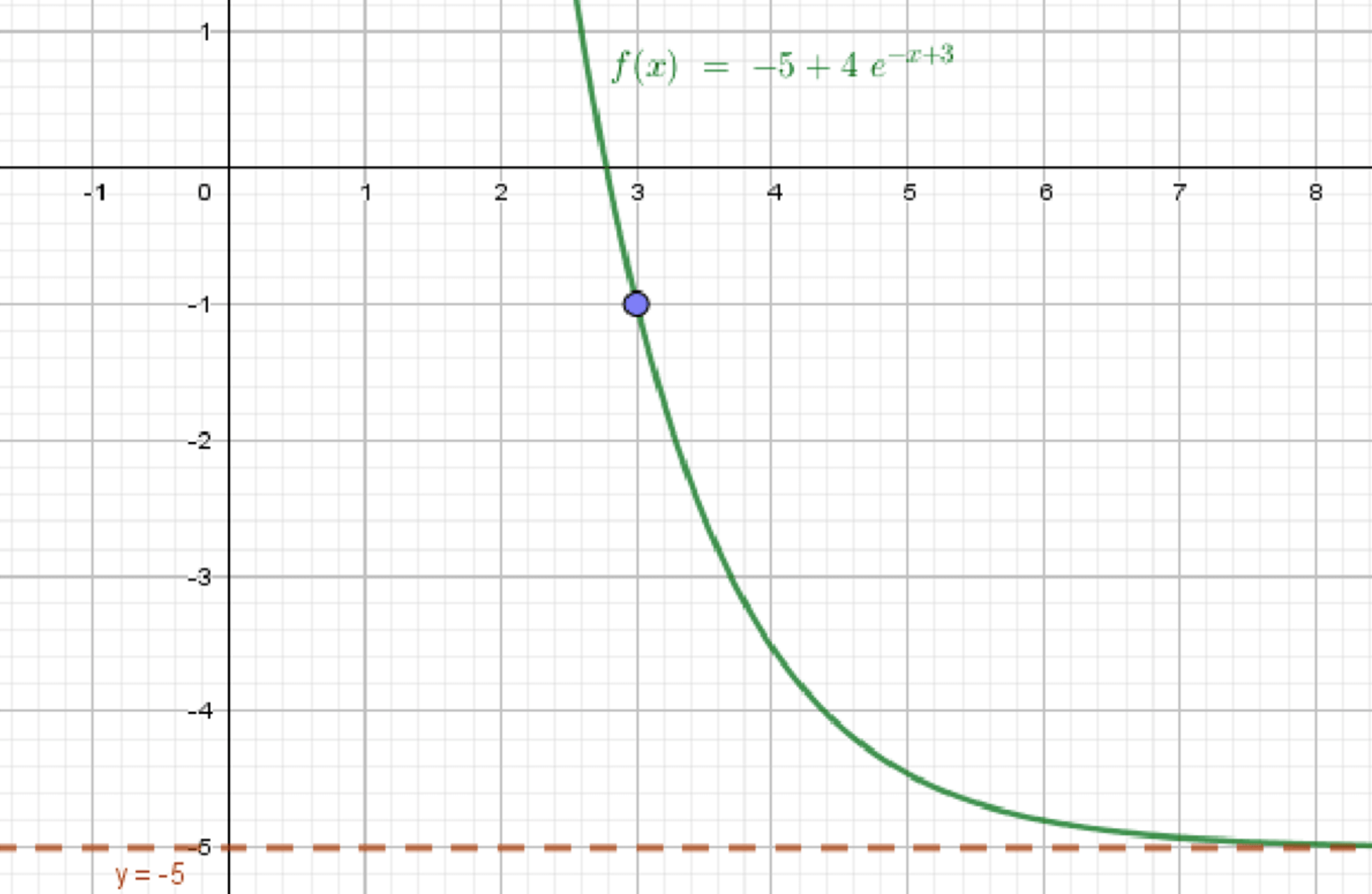
г) и
Что это значит:
- При : график плавно подходит к с обеих сторон.
- При : график приближается к горизонтальной асимптоте .
Как выглядит график:
- Вблизи : плавное приближение к значению .
- Далеко справа (большие ) — график становится почти горизонтальным и идёт вдоль .
Как построить:
- Проведите горизонтальную пунктирную линию .
- Нарисуйте кривую, которая вблизи идёт к значению .
- Затем график постепенно уходит вниз к асимптоте , как бы «сползая».
- В точке можно поставить точку или оставить дырку — условие не требует, чтобы было определено.