Учебник А.Г. Мордковича «Алгебра и начала математического анализа» давно стал классикой среди пособий для старшеклассников. Его популярность объясняется не только качественным содержанием, но и структурированным подходом к изучению сложных тем алгебры и математического анализа. Этот задачник является неотъемлемой частью учебного процесса для подготовки к экзаменам, включая ЕГЭ.
ГДЗ 10-11 Класс Номер 26.3 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы
Постройте эскиз графика какой-нибудь функции y = f(x), обладающей указанным свойством:
а) ;
б) ;
в) ;
г) .
Построить эскиз графика какой-нибудь функции , обладающей указанным свойством:
а) ;
б) ;
в) ;
г) .
Построить эскиз графика какой-нибудь функции , обладающей указанным свойством:
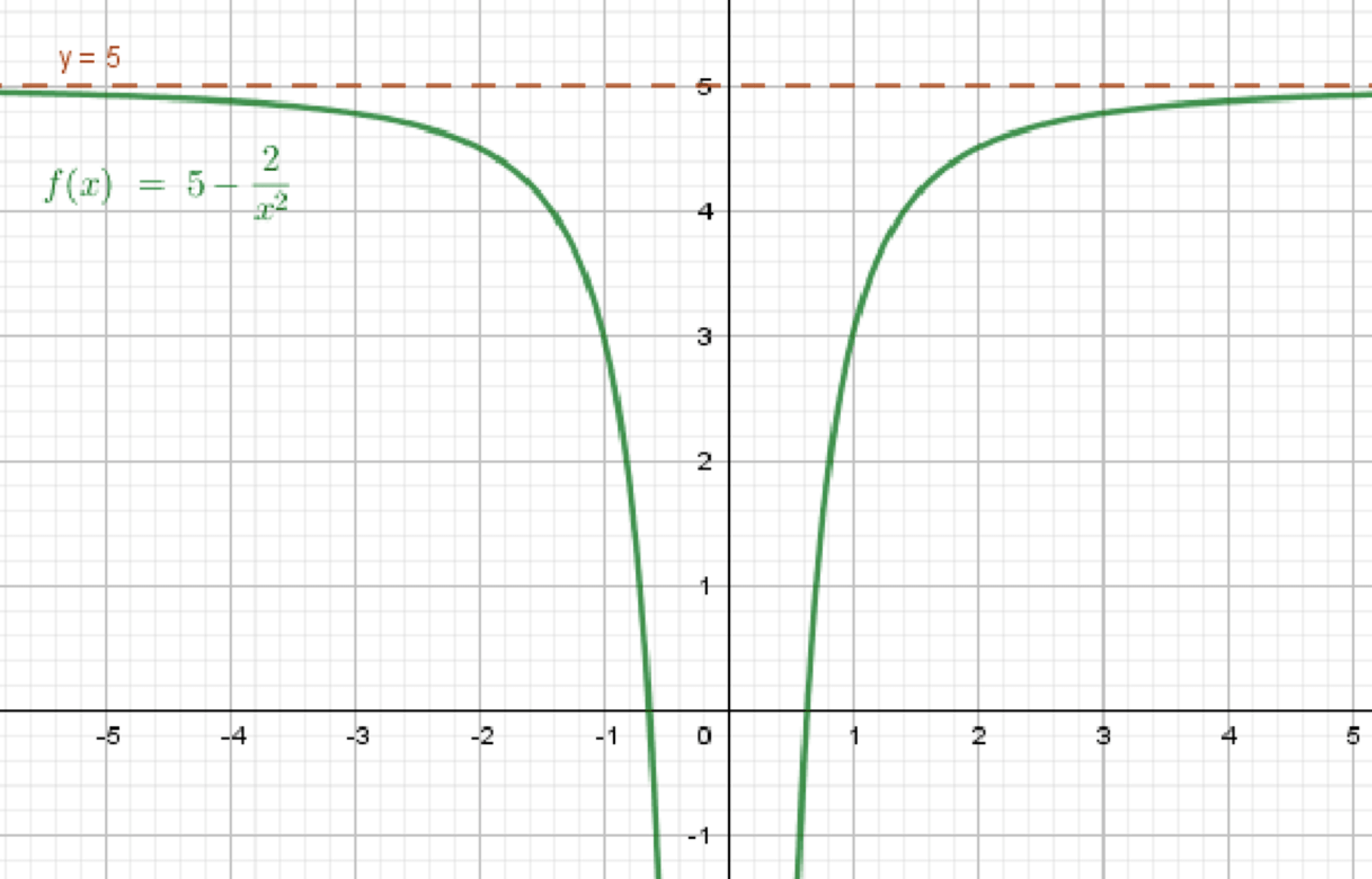
а)
1. Что означает это условие?
Это значит, что при больших значениях (то есть когда ), значения функции становятся всё ближе к числу 5, но не обязательно равны ему.
2. Пример функции:
3. Почему подходит:
Разделим числитель и знаменатель на :
4. Как построить график:
- Отметь горизонтальную асимптоту — пунктирной линией.
- Построй несколько точек функции:
- График сначала ниже уровня 5, затем медленно поднимается и приближается к 5, не пересекая асимптоту.
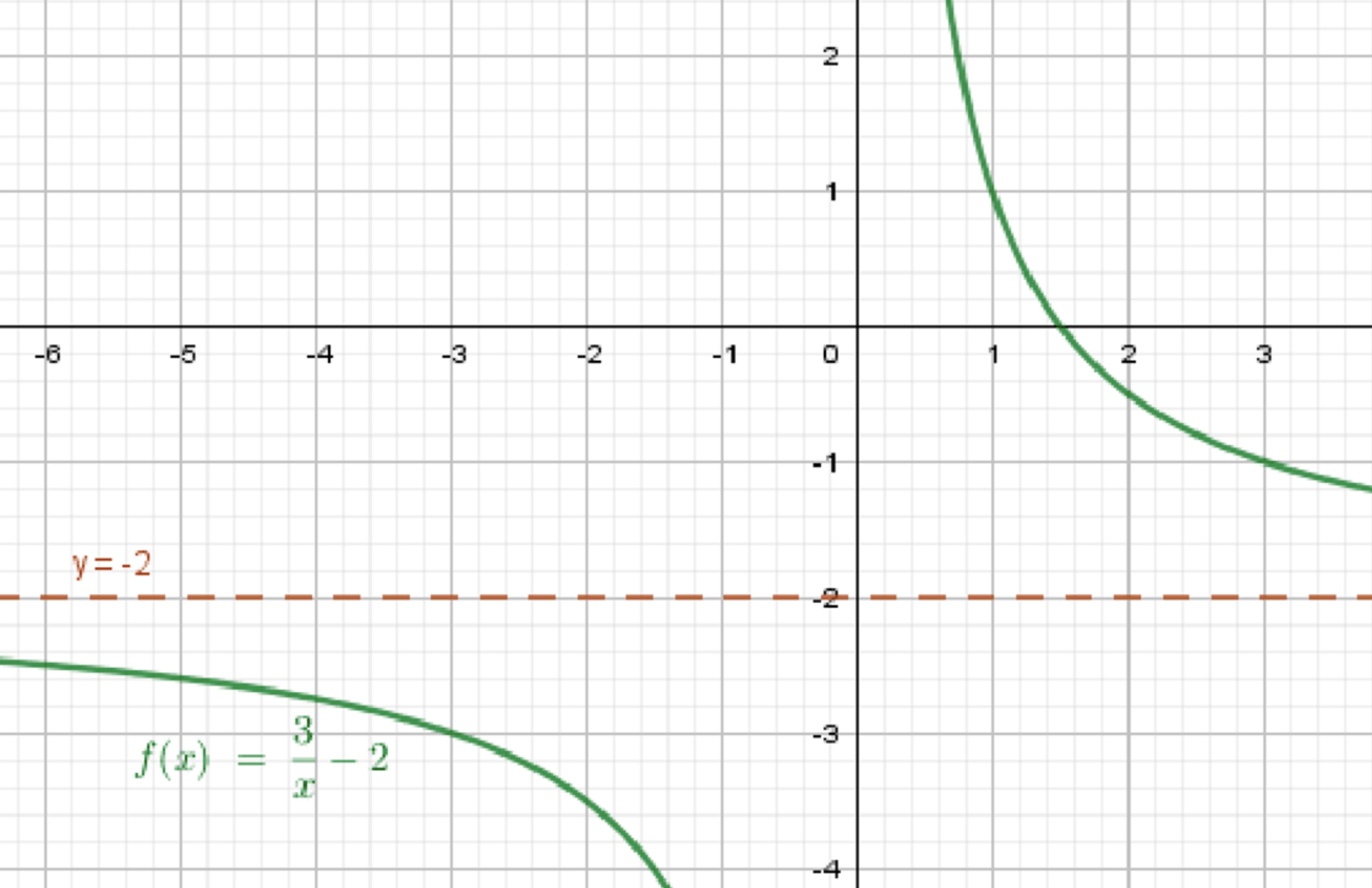
б)
1. Что означает это условие?
Функция приближается к значению –2, когда .
2. Пример функции:
3. Проверка предела:
4. Как построить график:
- Построй асимптоту .
- Точки:
- График спускается и приближается к –2, оставаясь выше.
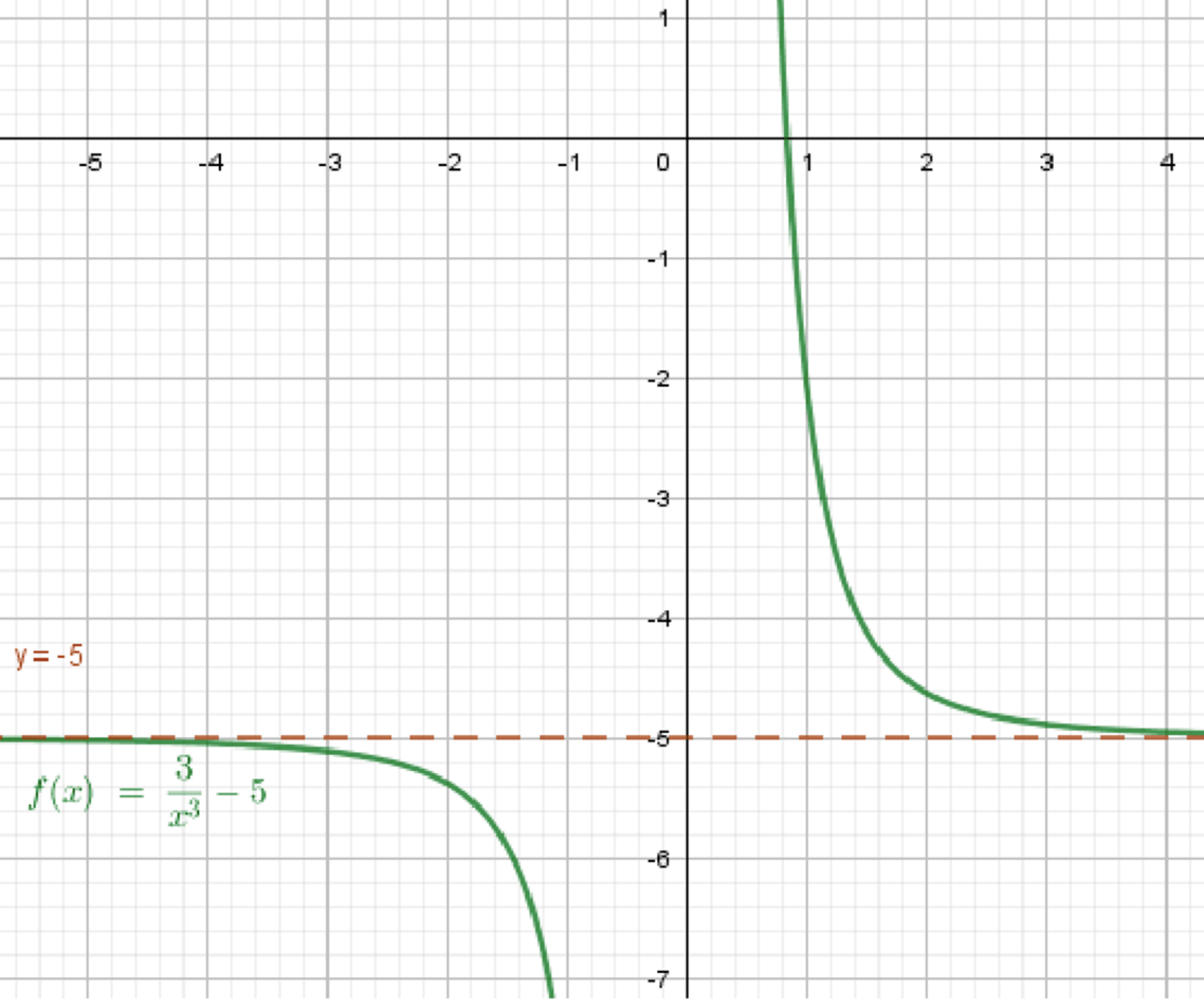
в)
1. Значение:
Значения приближаются к –5 при больших .
2. Пример:
3. Проверка:
4. Построение:
- Асимптота:
- Точки:
- График убывает к –5
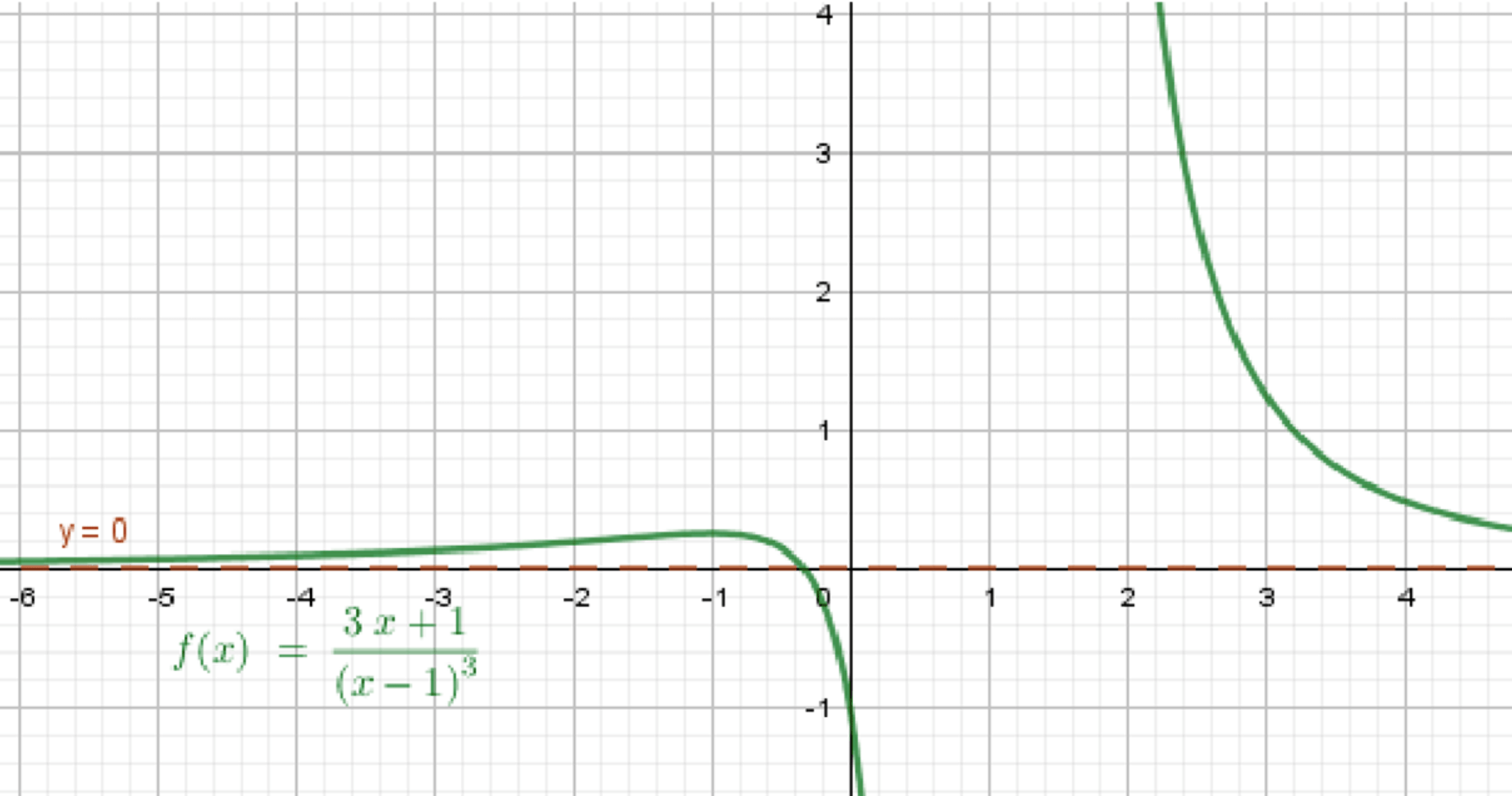
г)
1. Значение:
Функция стремится к нулю при
2. Пример:
3. Проверка:
4. Построение:
- Асимптота:
- Точки:
- График идёт сверху вниз, приближаясь к оси , но не пересекает её.