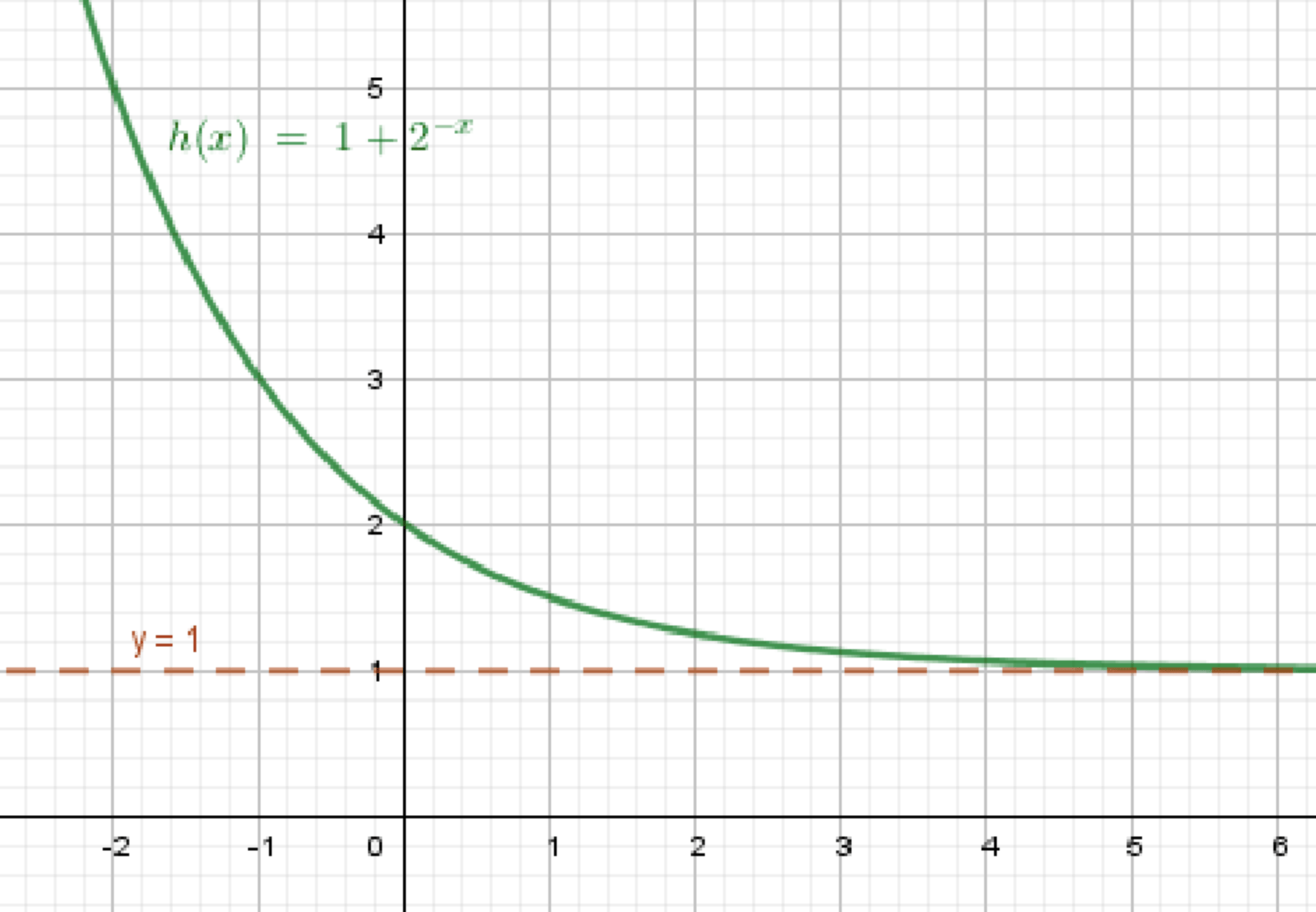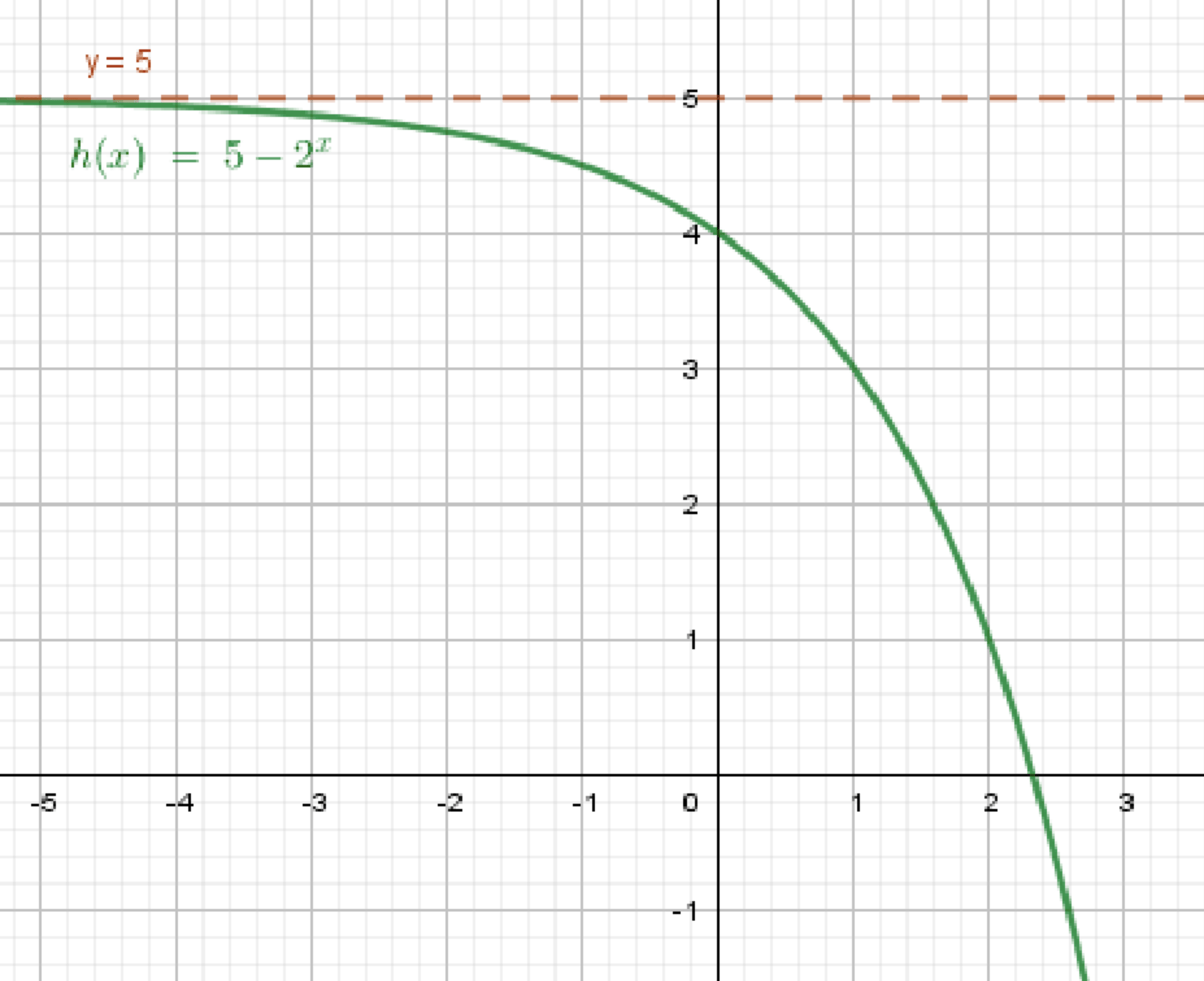ГДЗ 10-11 Класс Номер 26.5 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте эскиз графика какой-нибудь функции y = h(x), обладающей указанными свойствами:

а)

$$\lim_{x \to +\infty} h(x) = 4 \quad \text{и функция возрастает};$$

б)

$$\lim_{x \to +\infty} h(x) = 1 \quad \text{и функция ограничена снизу};$$

в)

$$\lim_{x \to -\infty} h(x) = 5 \quad \text{и функция убывает};$$

г)

$$\underset{x\to \mathrm{\infty }}{\lim }h(x)=1\text{и функция ограничена}\mathrm{.}$$

Построить эскиз графика какой-нибудь функции $y = h(x)$, обладающей указанными свойствами:

а)

$$\lim_{x \to +\infty} h(x) = 4 \quad \text{и функция возрастает};$$

б)

$$\lim_{x \to +\infty} h(x) = 1 \quad \text{и функция ограничена снизу};$$

в)

$$\lim_{x \to -\infty} h(x) = 5 \quad \text{и функция убывает};$$

г)

$$\lim_{x \to \infty} h(x) = 1 \quad \text{и функция ограничена}.$$

а)

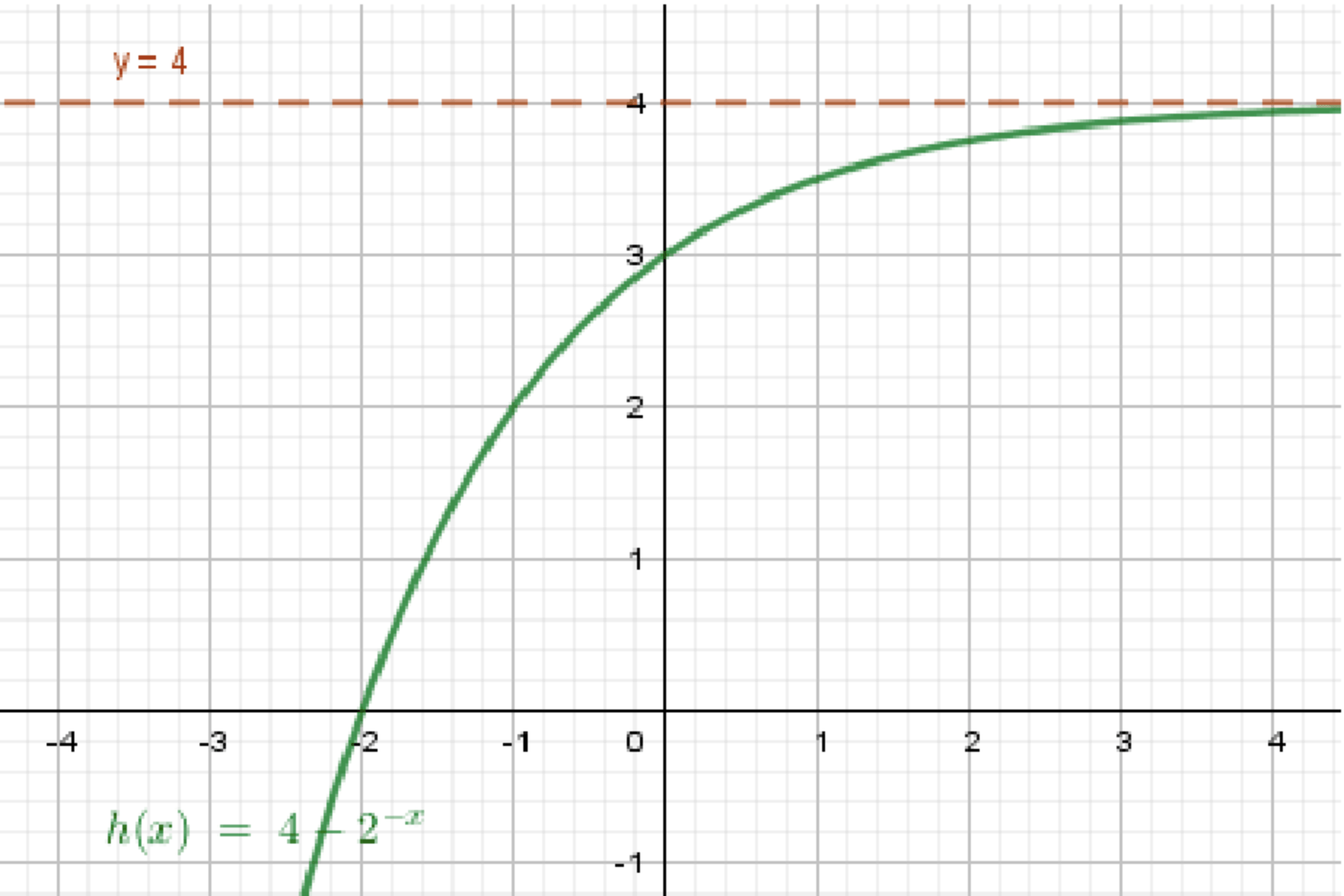
Условие:

$$\lim_{x \to +\infty} h(x) = 4 \quad \text{и функция возрастает}.$$

Анализ условий:

• Предел при $x \to +\infty$ равен 4 — значит, график «приближается» к горизонтальной прямой $y = 4$, но не обязательно достигает её.
• Функция возрастает — значит, при любом увеличении $x$, значение $h(x)$ тоже увеличивается.

Пример функции:

$$h(x) = 4 — \frac{1}{x + 1}$$

Почему подходит:

• При $x \to +\infty$, $\frac{1}{x + 1} \to 0$, значит $h(x) \to 4$;
• $h'(x) = \frac{1}{(x + 1)^2} > 0$, то есть функция возрастает.

Как строить график:

Нарисуй горизонтальную асимптоту: пунктирная линия $y = 4$.

Отметь несколько точек:

• $x = 0 \Rightarrow h(0) = 4 — 1 = 3$
• $x = 1 \Rightarrow h(1) = 4 — \frac{1}{2} = 3.5$
• $x = 4 \Rightarrow h(4) = 4 — \frac{1}{5} = 3.8$

Соединяй плавной кривой, монотонно растущей, приближающейся к $y = 4$ справа.

Как выглядит график:

Плавно поднимающаяся кривая, начинающаяся ниже $y = 4$, и бесконечно приближающаяся к нему справа. График никогда не пересекает асимптоту.

б)

Условие:

$$\lim_{x \to +\infty} h(x) = 1 \quad \text{и функция ограничена снизу}.$$

Анализ:

• Предел при $x \to +\infty$ равен 1.
• Ограничена снизу — есть нижняя граница, которую график не пересекает.

Пример функции:

$$h(x) = 1 + \frac{\sin x}{x + 2}$$

Почему подходит:

• $\frac{\sin x}{x + 2} \to 0$, а значит $h(x) \to 1$ при $x \to +\infty$;
• $\sin x \in [-1, 1]$, поэтому $h(x) \in \left[1 — \frac{1}{x + 2}, 1 + \frac{1}{x + 2}\right]$, и минимум по $x \ge 0$ не ниже $0.5$, скажем.

Как строить график:

Нарисуй горизонтальную асимптоту $y = 1$.

На $x \in [0, 10]$, отрисуй слегка колеблющуюся волну, затухающую к значению 1.

График будет слегка «вибрировать» вокруг 1, но никогда не пересечёт нижнюю границу, например, 0.5.

Как выглядит график:

Колеблющаяся кривая, постепенно затухающая и приближающаяся к прямой $y = 1$. Нижняя граница строго выше, например, 0.5.

в)

Условие:

$$\lim_{x \to -\infty} h(x) = 5 \quad \text{и функция убывает}.$$

Анализ:

• Предел при $x \to -\infty$ равен 5.
• Функция убывает — при увеличении $x$, значение $h(x)$ убывает.

Пример функции:

$$h(x) = 5 + \frac{1}{x}$$

Почему подходит:

• При $x \to -\infty$, $\frac{1}{x} \to 0$, значит $h(x) \to 5$;
• $h'(x) = -\frac{1}{x^2} < 0$, значит функция убывает.

Как строить график:

Нарисуй асимптоту $y = 5$.

Отметь точки для отрицательных $x$:

• $x = -1 \Rightarrow h(x) = 5 — 1 = 4$
• $x = -10 \Rightarrow h(x) = 5 — 0.1 = 4.9$

Нарисуй плавно убывающий график слева направо, стремящийся к 5 при $x \to -\infty$.

Как выглядит график:

Кривая, начинающаяся слева от оси $x$, идёт сверху вниз, приближаясь к $y = 5$ слева.

г)

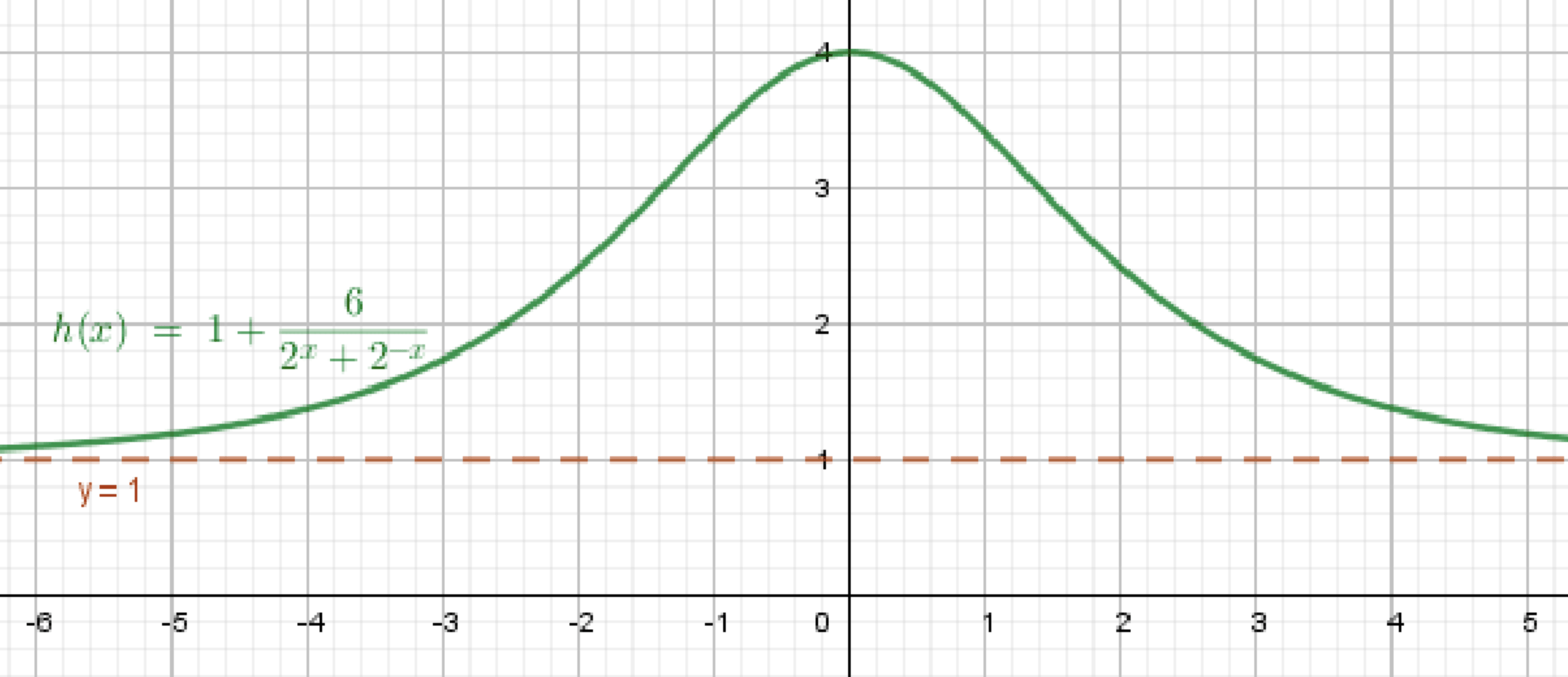
Условие:

$$\lim_{x \to \infty} h(x) = 1 \quad \text{и функция ограничена}.$$

Анализ:

• Предел при $x \to \infty$ равен 1.
• Функция ограничена — значит, значения $h(x)$ не выходят за определённый диапазон.

Пример функции:

$$h(x) = 1 + \frac{\sin x}{x}$$

Почему подходит:

• $\frac{\sin x}{x} \to 0$, а значит $h(x) \to 1$;
• $\sin x \in [-1, 1] \Rightarrow h(x) \in \left[1 — \frac{1}{x}, 1 + \frac{1}{x}\right]$, т.е. функция ограничена.

Как строить график:

Нарисуй асимптоту $y = 1$.

Отметь несколько точек:

• $x = 1 \Rightarrow h(x) = 1 + \sin(1) \approx 1.84$
• $x = 10 \Rightarrow h(x) \approx 1 \pm 0.1$

Нарисуй волнистый график, амплитуда которого затухает к 0, приближаясь к 1.

Как выглядит график:

Затухающие колебания вокруг $y = 1$, не выходящие за рамки (например) $[0.5; 1.5]$.