ГДЗ 10-11 Класс Номер 26.7 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

а) $$$\lim_{x \to +\infty} f(x) = 5$ и $f(x) > 0$ на $(-\infty; +\infty)$;

б) $$$\lim_{x \to -\infty} f(x) = -3$ и $f(x) \geq 0$ на $[-7; 3]$;

в) $$$\lim_{x \to +\infty} f(x) = 0$ и $f(x) > 0$ на $[0; +\infty)$;

г) ${}_{}$$\lim_{x \to -\infty} f(x) = 0$ и $f(x) < 0$ на $(-\infty; +\infty)$.

Построить эскиз графика какой-нибудь функции $y = f(x)$, обладающей указанными свойствами:

а) $$$\lim_{x \to +\infty} f(x) = 5$ и $f(x) > 0$ на $(-\infty; +\infty)$;

б) $$$\lim_{x \to -\infty} f(x) = -3$ и $f(x) \geq 0$ на $[-7; 3]$;

в) $$$\lim_{x \to +\infty} f(x) = 0$ и $f(x) > 0$ на $[0; +\infty)$;

г) ${}_{}$$\lim_{x \to -\infty} f(x) = 0$ и $f(x) < 0$ на $(-\infty; +\infty)$.

а)

Условия:

• $\displaystyle \lim_{x \to +\infty} f(x) = 5$;
• $f(x) > 0$ на $(-\infty; +\infty)$.

Выбор функции:

Подойдёт, например:

$$f(x) = 5 — \frac{4}{x^2 + 1}$$

Пояснение:

• При $x \to +\infty$:
  $\frac{4}{x^2 + 1} \to 0$, значит $f(x) \to 5$.
• $f(x) > 0$, потому что:
  • знаменатель положителен;
  • $\frac{4}{x^2 + 1} < 4$, значит $f(x) > 5 — 4 = 1 > 0$.

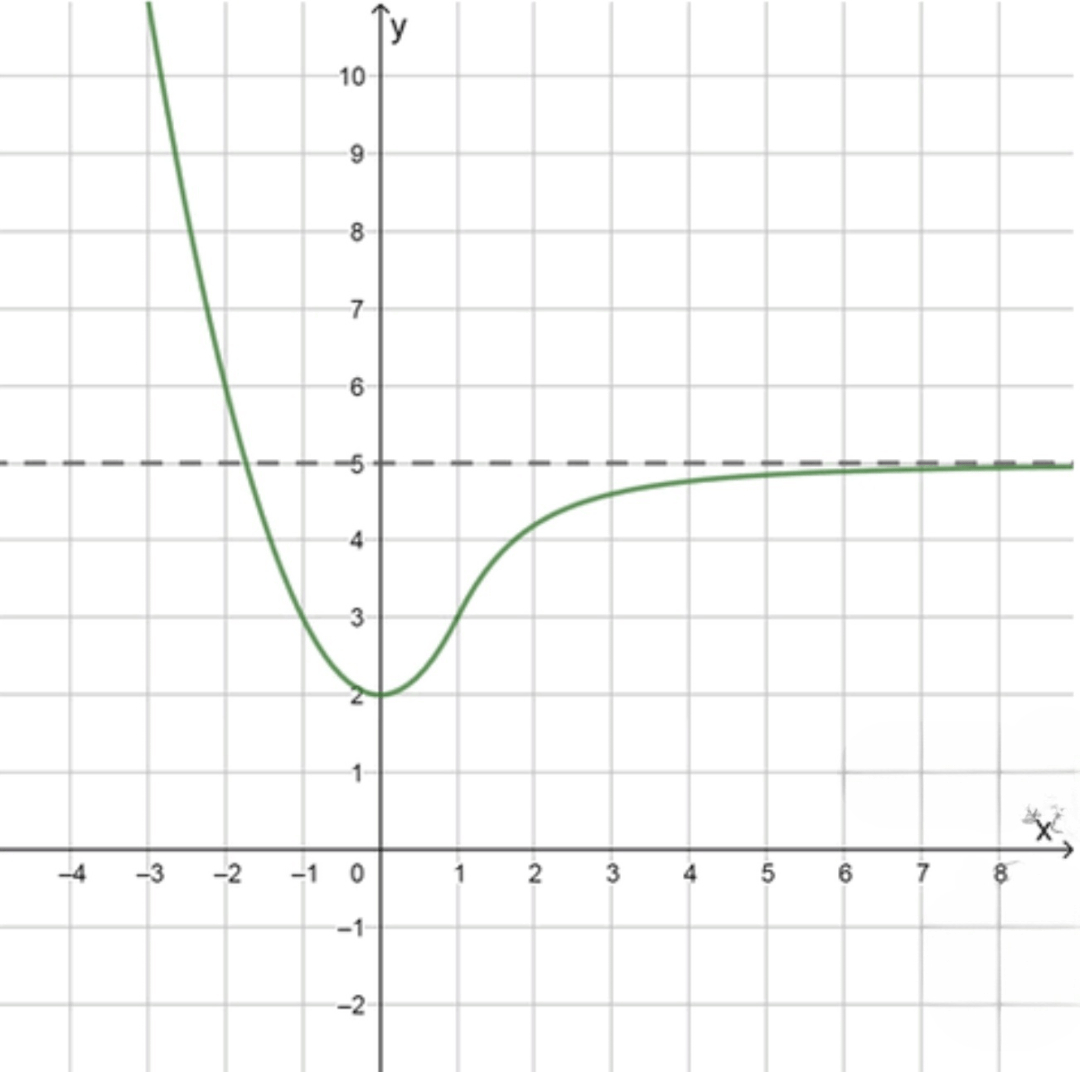
Как выглядит график:

• Плавная кривая, асимптотически приближается к $y = 5$ при $x \to +\infty$;
• График всегда выше оси $x$, лежит в положительной области по $y$;
• Симметричен относительно оси $y$, минимум в точке $x = 0$: $f(0) = 1$.

б)

Условия:

• $\displaystyle \lim_{x \to -\infty} f(x) = -3$;
• $f(x) \geq 0$ на отрезке $[-7; 3]$.

Выбор функции:

Пусть

$$f(x) = \begin{cases} (x + 3)^2, & x \in [-7; 3] \\ -3 + \frac{1}{(x + 8)^2}, & x < -7 \end{cases}$$

Пояснение:

• На $[-7; 3]$ функция — квадратный трёхчлен, всегда $\geq 0$.
• При $x \to -\infty$: $\frac{1}{(x + 8)^2} \to 0$, значит $f(x) \to -3$.
• Плавно спадает слева, асимптотически стремясь к $-3$.

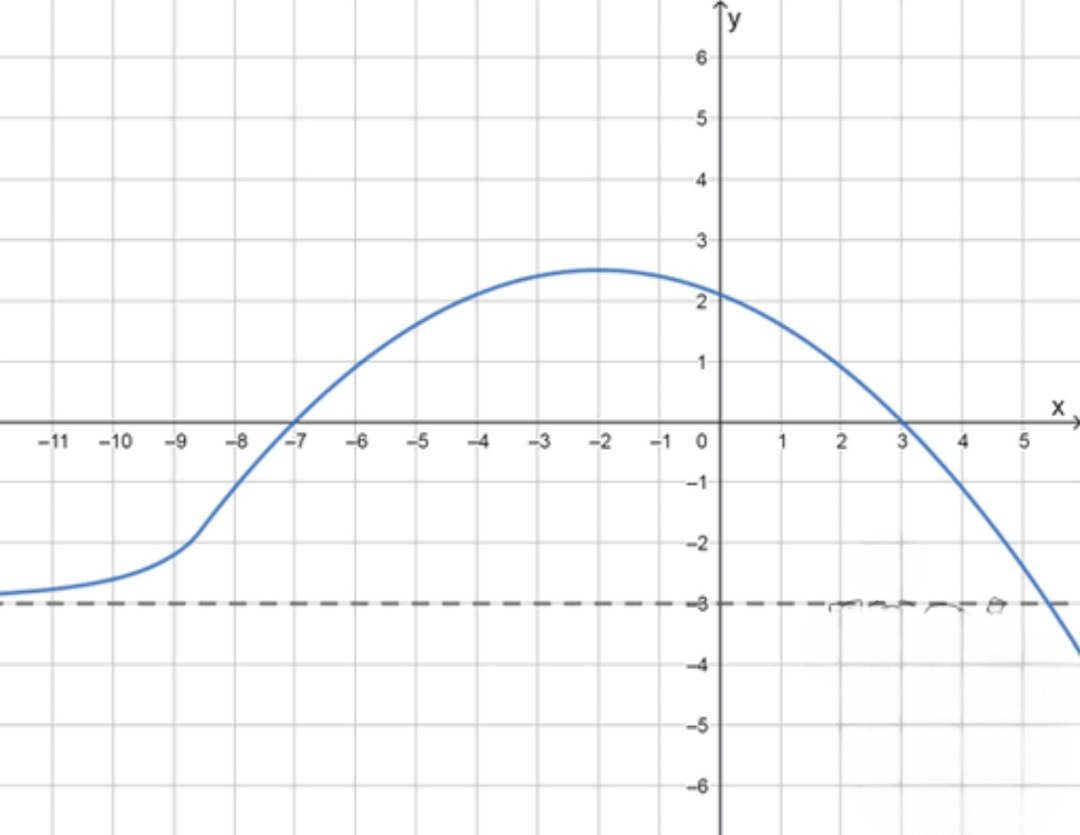
Как выглядит график:

• На $[-7; 3]$: парабола вверх (неотрицательная);
• При $x < -7$: уходит вниз, асимптотически приближается к $y = -3$;
• График разрывен в $x = -7$, но непротиворечив.

в)

Условия:

• $\displaystyle \lim_{x \to +\infty} f(x) = 0$;
• $f(x) > 0$ на $[0; +\infty)$.

Выбор функции:

Пусть

$$f(x) = \frac{1}{x + 1}$$

Пояснение:

• При $x \to +\infty$: $f(x) \to 0$;
• На $[0; +\infty)$: $x + 1 > 0$, значит $f(x) > 0$.

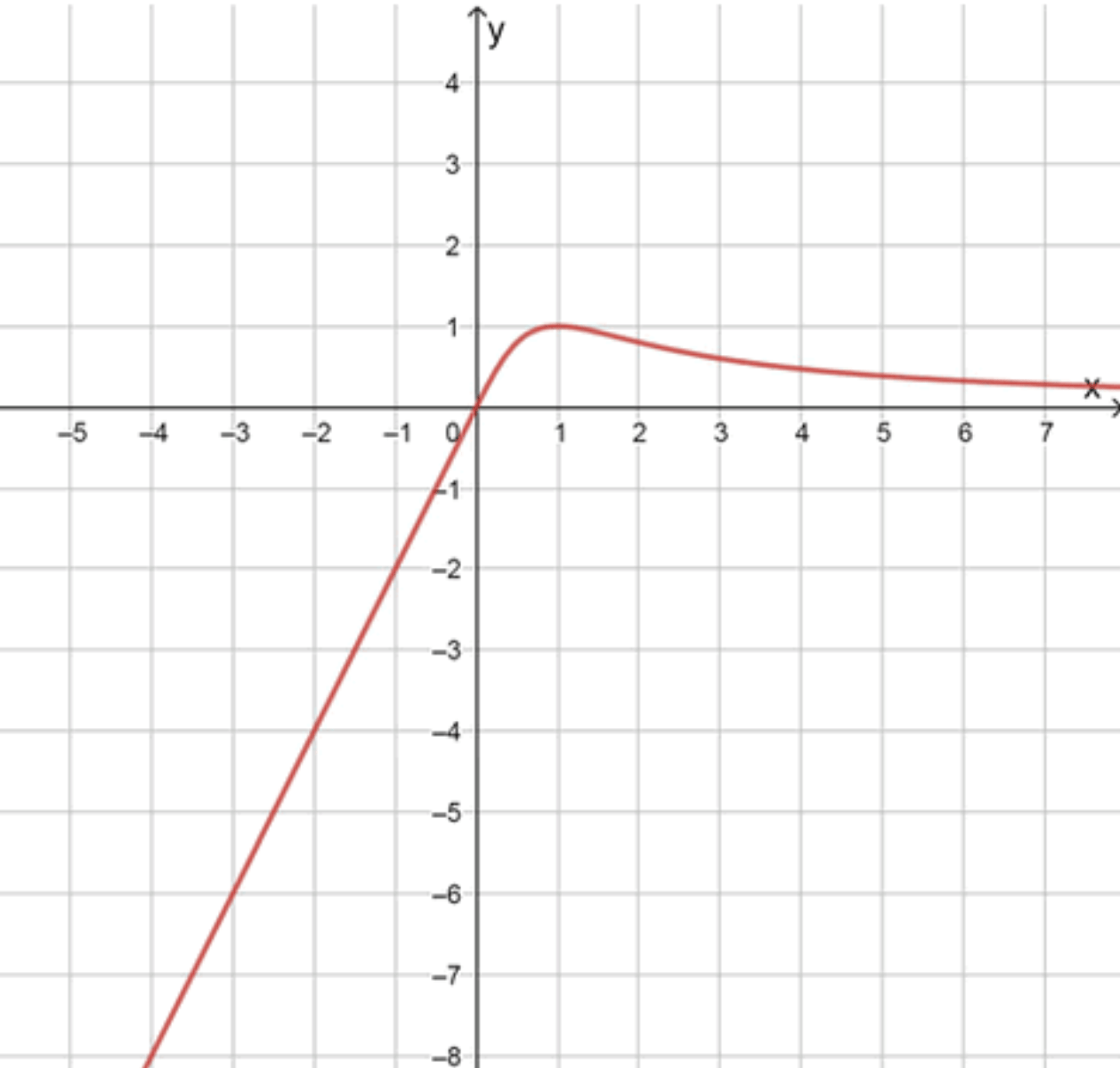
Как выглядит график:

• Начинается в точке $(0; 1)$;
• Плавно убывает вправо;
• График лежит в первой четверти, приближаясь к оси $x$, но не пересекает её.

г)

Условия:

• $\displaystyle \lim_{x \to -\infty} f(x) = 0$;
• $f(x) < 0$ на $(-\infty; +\infty)$.

Выбор функции:

Пусть

$$f(x) = -\frac{1}{x^2 + 1}$$

Пояснение:

• $x^2 + 1 > 0 \Rightarrow f(x) < 0$ при любом $x$;
• При $x \to -\infty$: $f(x) \to 0^-$;
• Также при $x \to +\infty$: тоже $f(x) \to 0^-$, но это не мешает, ведь условие только на $x \to -\infty$.

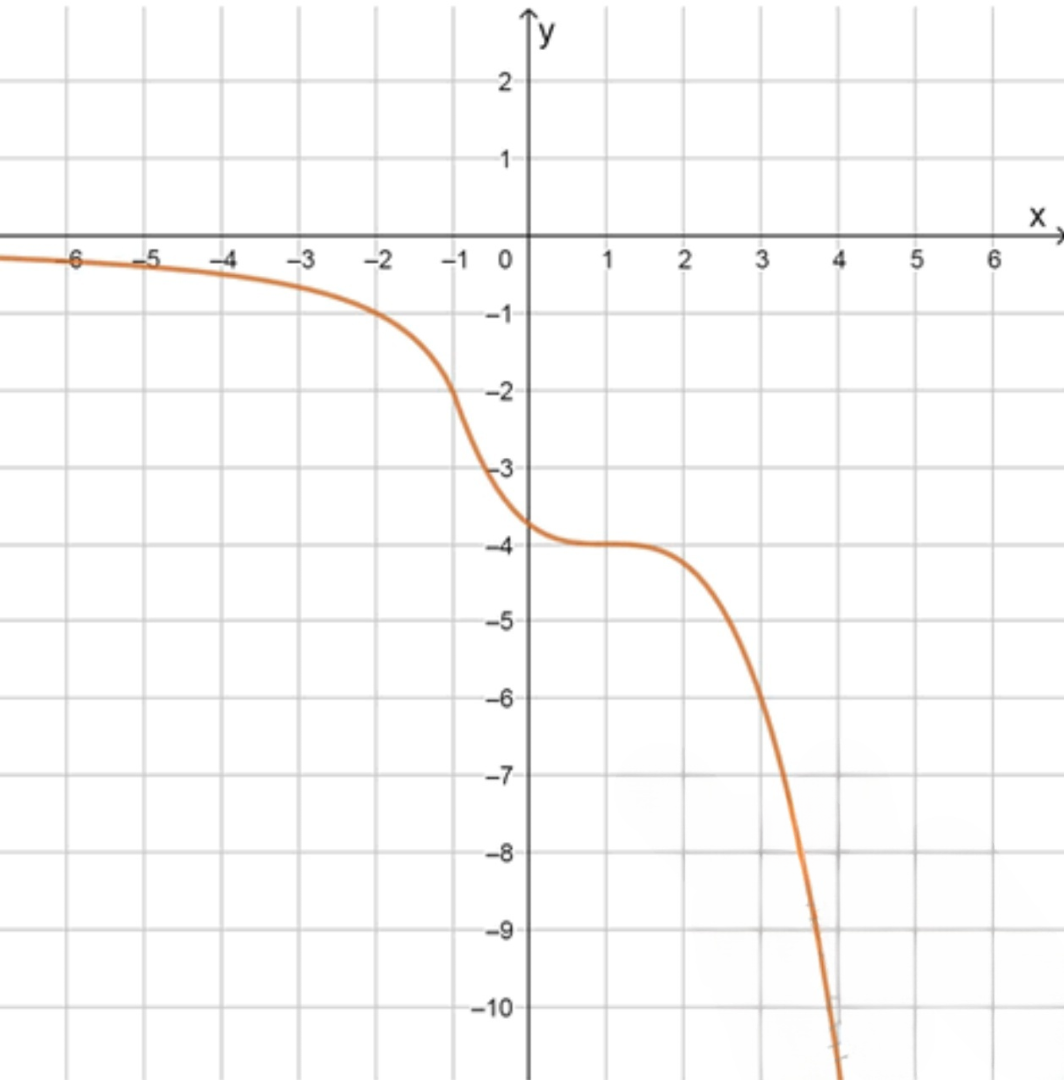
Как выглядит график:

• Симметричен относительно оси $y$;
• Всегда под осью $x$;
• Минимум в $x = 0$: $f(0) = -1$;
• При $x \to \pm\infty$: приближается к $y = 0$ снизу.