ГДЗ 10-11 Класс Номер 26.8 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте эскиз графика какой-нибудь функции у = h(x), х принадлежит R, обладающей указанными свойствами:

а) $\lim_{x \to +\infty} h(x) = 4$ и функция возрастает;

б) $\lim_{x \to -\infty} h(x) = 5$ и функция убывает;

в) $\lim_{x \to -\infty} h(x) = -2$ и функция возрастает;

г) $\lim_{x \to +\infty} h(x) = -3$ и функция убывает.

Построить эскиз графика какой-нибудь функции $y = h(x)$, обладающей указанными свойствами:

а) $\lim_{x \to +\infty} h(x) = 4$ и функция возрастает;

б) $\lim_{x \to -\infty} h(x) = 5$ и функция убывает;

в) $\lim_{x \to -\infty} h(x) = -2$ и функция возрастает;

г) $\lim_{x \to +\infty} h(x) = -3$ и функция убывает.

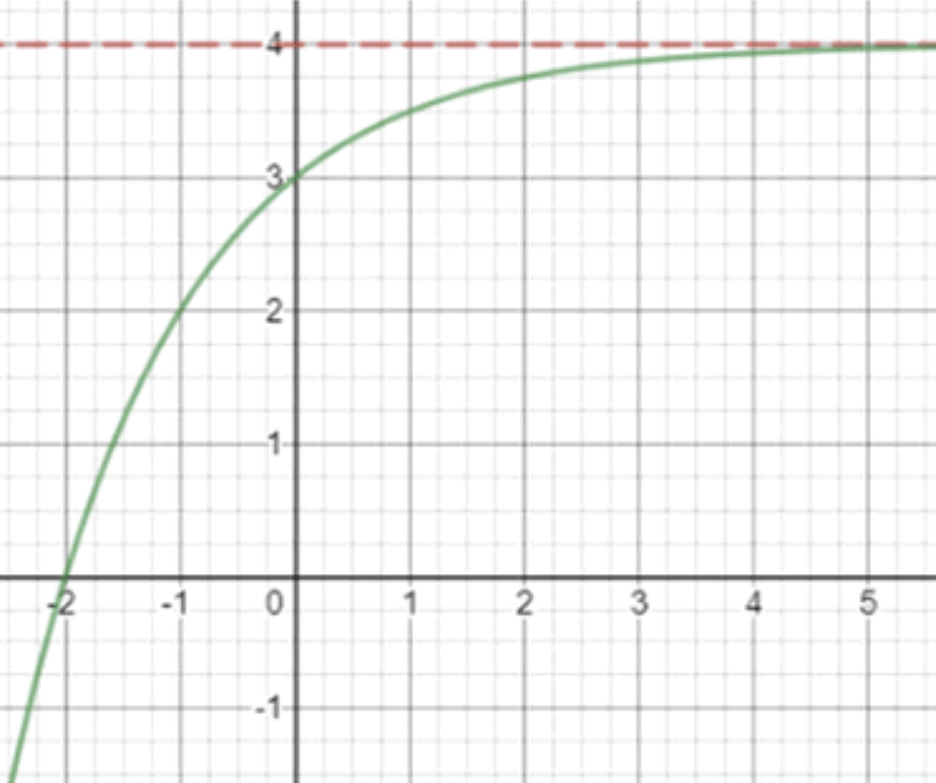
а) $\lim_{x \to +\infty} h(x) = 4$, функция возрастает

Пояснение:

• Функция возрастает, т.е. чем больше $x$, тем больше $h(x)$.
• Но предел при $x \to +\infty$ равен 4 — значит, функция приближается к 4 сверху, но никогда не превышает 4 (иначе она не возрастала бы до предела, а прошла бы его).
• Это возможно только если функция возрастает и стремится к 4, не достигая этого значения.

Пример функции:

$$h(x) = 4 — \frac{1}{x}$$

Для $x > 0$ функция:

• возрастает (так как $\frac{1}{x}$ убывает),
• при $x \to +\infty$: $\frac{1}{x} \to 0$, значит $h(x) \to 4$.

Как построить:

1. Нарисуй горизонтальную асимптоту: прямая $y = 4$.
2. Построй точку при $x = 1$: $h(1) = 4 — 1 = 3$.
3. При $x = 10$: $h(10) = 4 — 0.1 = 3.9$, и так далее.
4. Соединяй точки плавной кривой, приближающейся к 4 справа.

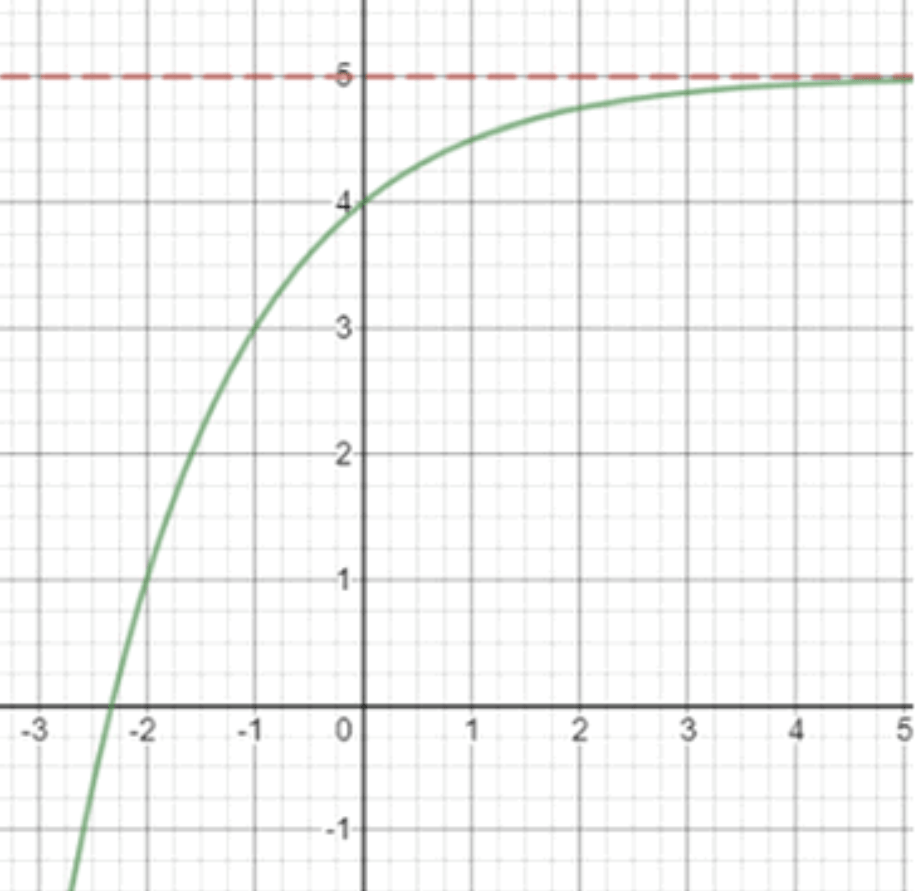
б) $\lim_{x \to -\infty} h(x) = 5$, функция убывает

Пояснение:

• При $x \to -\infty$, $h(x) \to 5$.
• При этом функция убывает, значит значения становятся всё меньше при увеличении $x$.
• Это возможно, если на бесконечном отрицательном промежутке функция приближается к 5 сверху, а затем продолжает уменьшаться.

Пример функции:

$$h(x) = 5 + \frac{1}{x}$$

Функция:

• убывает (так как $\frac{1}{x}$ убывает при $x < 0$),
• при $x \to -\infty$: $\frac{1}{x} \to 0$, значит $h(x) \to 5$.

Как построить:

1. Проведи горизонтальную прямую $y = 5$.
2. Построй точки: $x = -1 \Rightarrow h = 4$, $x = -10 \Rightarrow h = 4.9$, и т.д.
3. Функция идёт сверху вниз, плавно стремится к 5 слева.

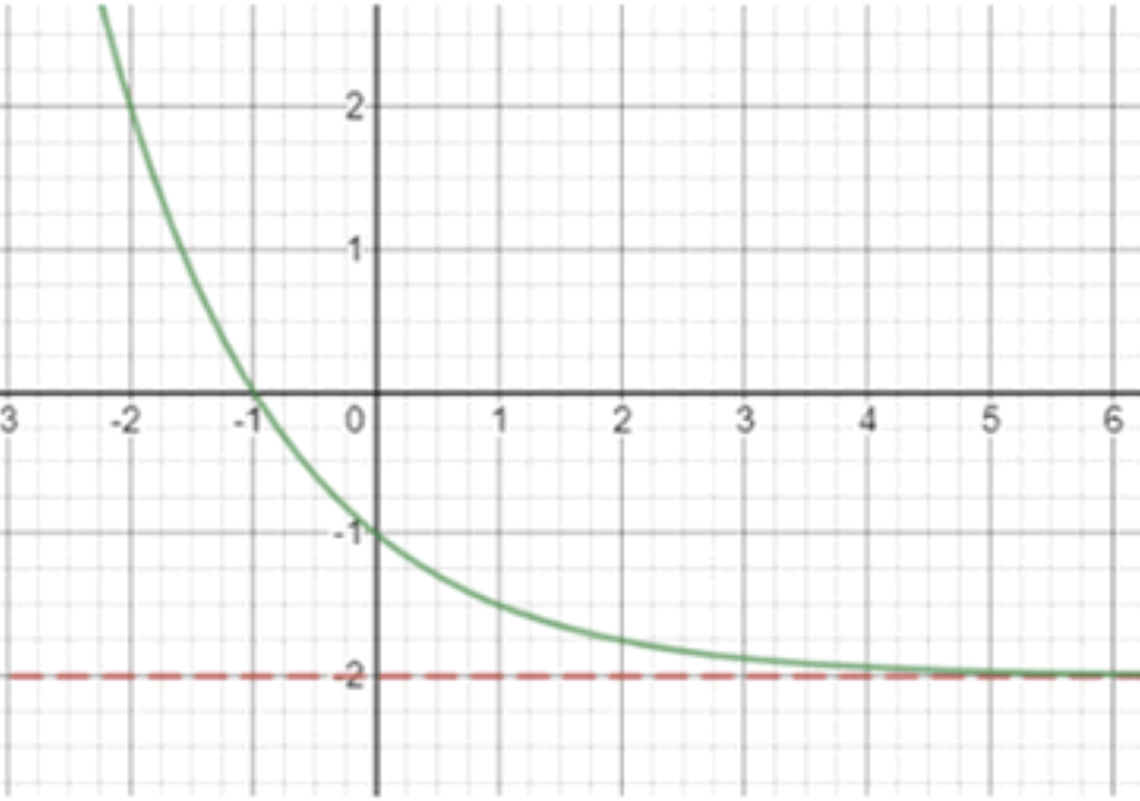
в) $\lim_{x \to -\infty} h(x) = -2$, функция возрастает

Пояснение:

• При $x \to -\infty$, $h(x) \to -2$, значит функция на бесконечном отрицательном участке приближается к -2.
• При этом она возрастает, т.е. идёт снизу вверх.

Пример функции:

$$h(x) = -2 + \frac{1}{x^2}$$

Функция:

• при $x \to -\infty$, $\frac{1}{x^2} \to 0$,
• $h(x) \to -2$,
• возрастает на $x < 0$ (так как $\frac{1}{x^2}$ убывает).

Как построить:

1. Нарисуй горизонтальную асимптоту $y = -2$.
2. Отметь точки: $x = -1 \Rightarrow h = -1$, $x = -10 \Rightarrow h \approx -1.99$.
3. Плавная возрастающая кривая снизу вверх.

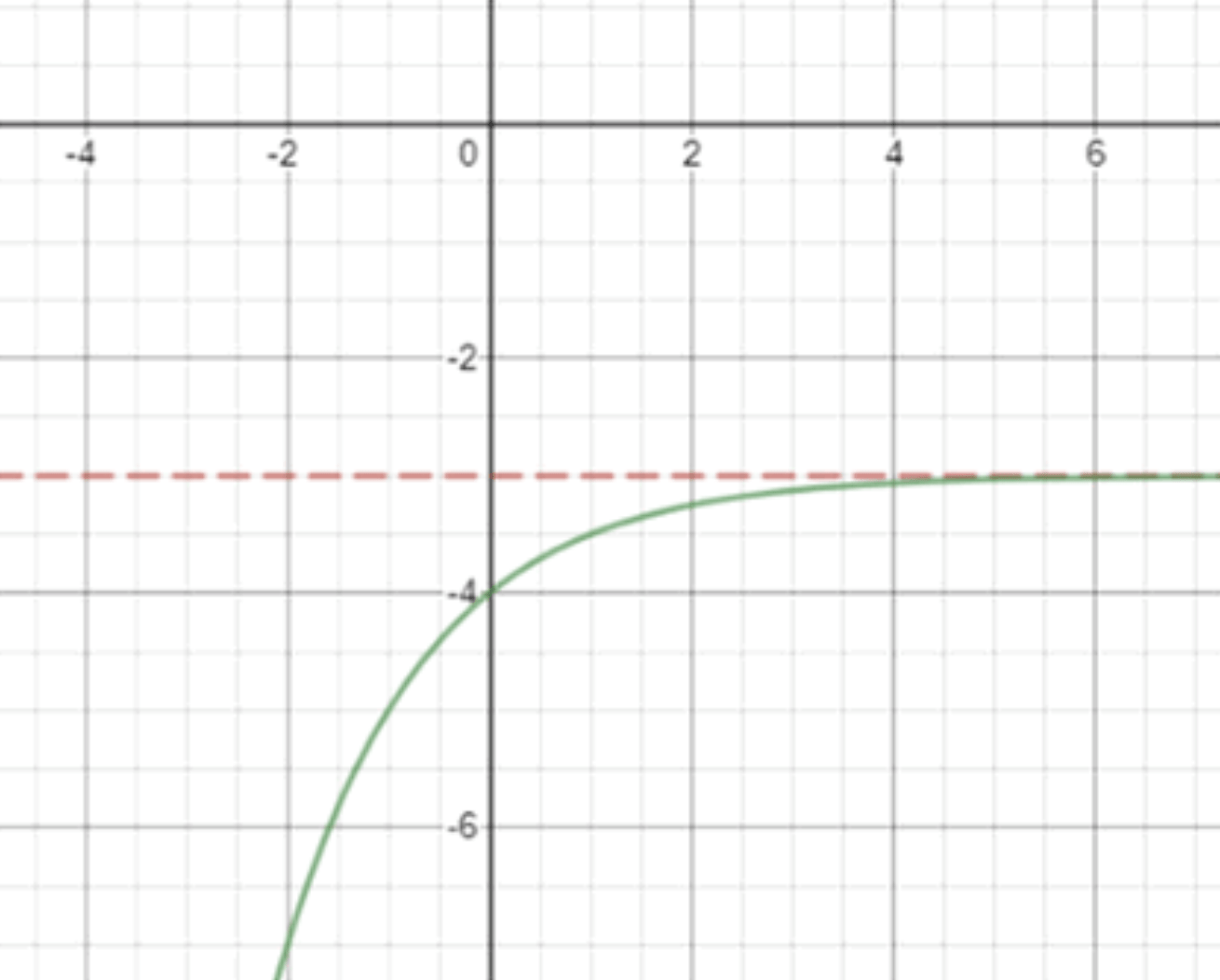
г) $\lim_{x \to +\infty} h(x) = -3$, функция убывает

Пояснение:

• Значит при $x \to +\infty$, функция стремится к -3.
• При этом она убывает, то есть идёт сверху вниз.

Пример функции:

$$h(x) = -3 + \frac{1}{x}$$

• При $x \to +\infty$, $h(x) \to -3$,
• Функция убывает, так как $\frac{1}{x}$ убывает.

Как построить:

1. Построить горизонтальную прямую $y = -3$.
2. При $x = 1 \Rightarrow h = -2$, при $x = 10 \Rightarrow h = -2.9$, и т.д.
3. Проведи плавную убывающую кривую, стремящуюся к -3 справа.