ГДЗ 10-11 Класс Номер 26.9 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

а) $\lim_{x \to -\infty} h(x) = 1$ и функция ограничена сверху;

б) $\lim_{x \to +\infty} h(x) = 1$ и функция ограничена снизу;

в) $\lim_{x \to \infty} h(x) = -2$ и функция ограничена;

г) $\lim_{x \to \infty} h(x) = 1$ и функция ограничена.

Построить эскиз графика какой-нибудь функции $y = h(x)$, обладающей указанными свойствами:

а) $\lim_{x \to -\infty} h(x) = 1$ и функция ограничена сверху;

б) $\lim_{x \to +\infty} h(x) = 1$ и функция ограничена снизу;

в) $\lim_{x \to \infty} h(x) = -2$ и функция ограничена;

г) $\lim_{x \to \infty} h(x) = 1$ и функция ограничена.

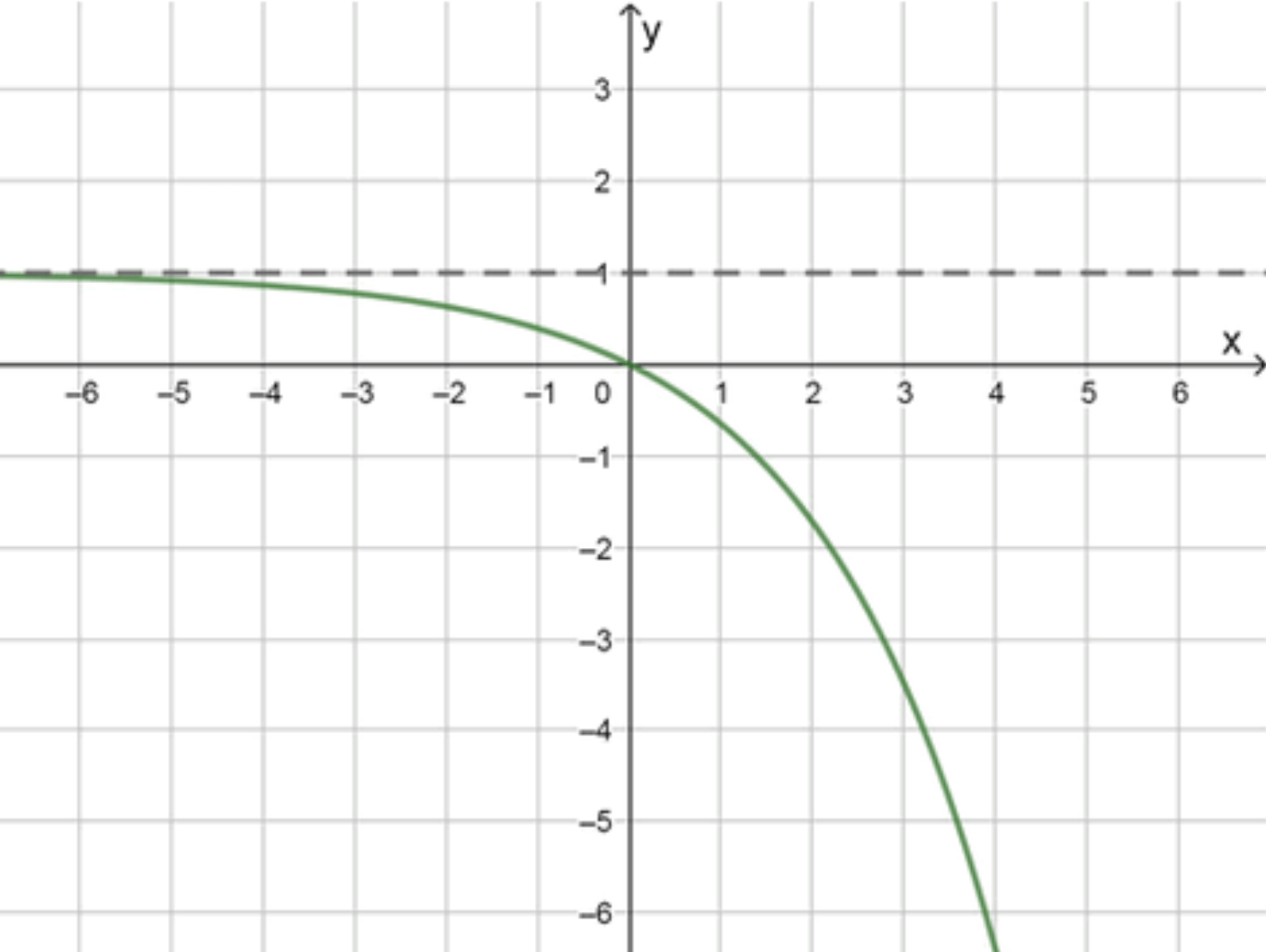
а) $\lim_{x \to -\infty} h(x) = 1$ и функция ограничена сверху

Выбор функции:

$$h(x) = 1 — \frac{1}{x^2 + 1}$$

Почему подходит:

• При $x \to -\infty$, $\frac{1}{x^2 + 1} \to 0$, значит $h(x) \to 1$.
• $\frac{1}{x^2 + 1} > 0$ ⇒ $h(x) < 1$ всегда, то есть ограничена сверху значением 1.

Инструкция по построению:

Нарисуйте горизонтальную линию $y = 1$ — асимптоту.

Постройте точки:

• $x = 0$: $h(0) = 1 — 1 = 0$
• $x = \pm1$: $h(\pm1) = 1 — \frac{1}{2} = 0.5$

Проведите плавную кривую под линией $y = 1$, возрастающую с обеих сторон и стремящуюся к 1 при $x \to -\infty$ и $x \to +\infty$.

Как выглядит: диагонально сниженная “чаша” под асимптотой $y=1$, с минимумом у $x=0$.

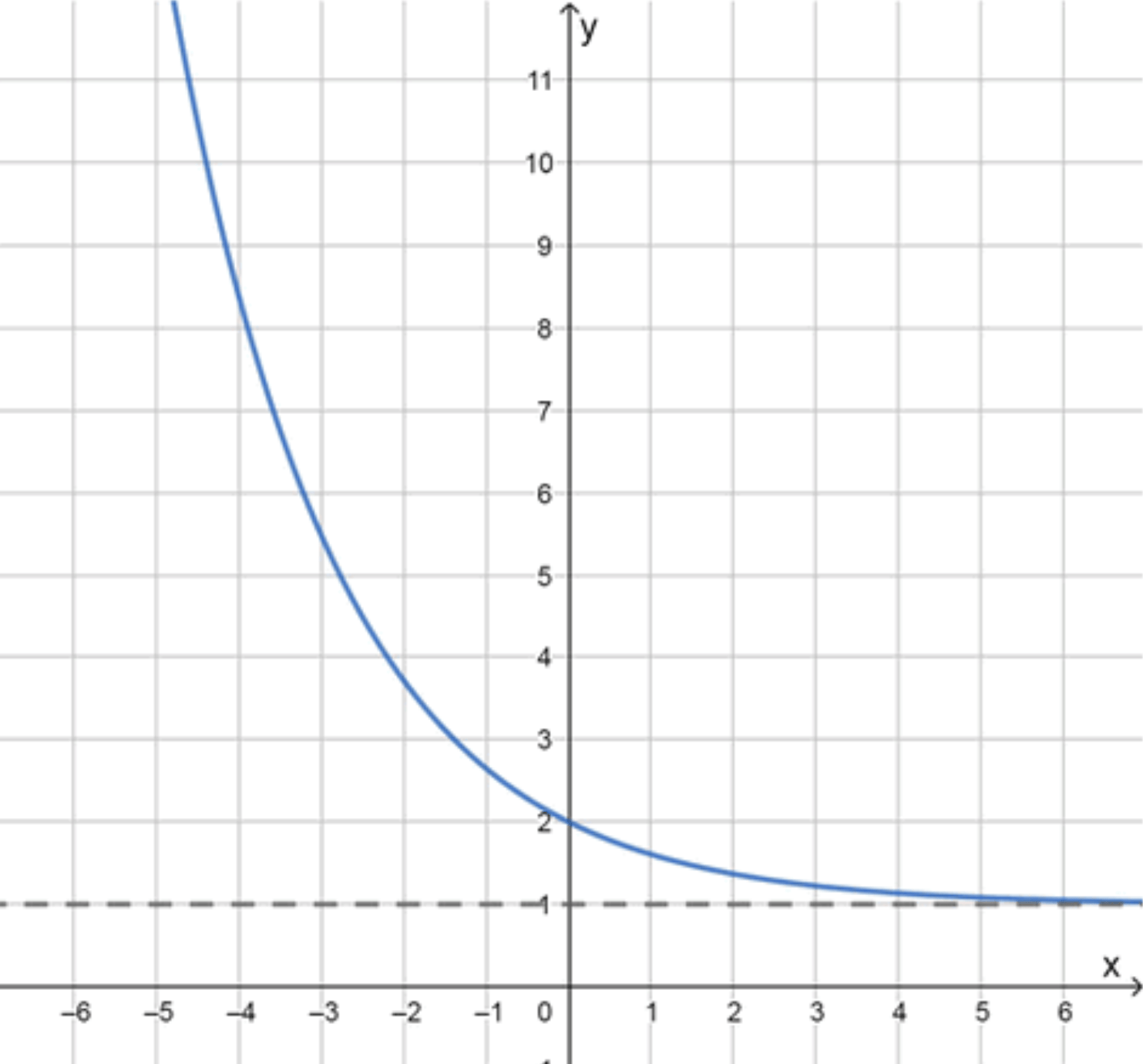
б) $\lim_{x \to +\infty} h(x) = 1$ и функция ограничена снизу

Выбор функции:

$$h(x) = 1 + \frac{1}{x^2 + 1}$$

Почему подходит:

• При $x \to +\infty$, $\frac{1}{x^2 + 1} \to 0$, значит $h(x) \to 1$.
• $h(x) > 1$, то есть ограничена снизу значением 1.

Построение:

Асимптота: $y = 1$.

Точки:

• $x = 0$: $h(0) = 2$
• $x = \pm1$: $h(\pm1) = 1.5$

Нарисуйте плавную кривую над $y = 1$, стремясь к ней при $x \to \pm\infty$.

Как выглядит: купол, открытый вверх, над уровнем $y=1$, с максимумом в центре.

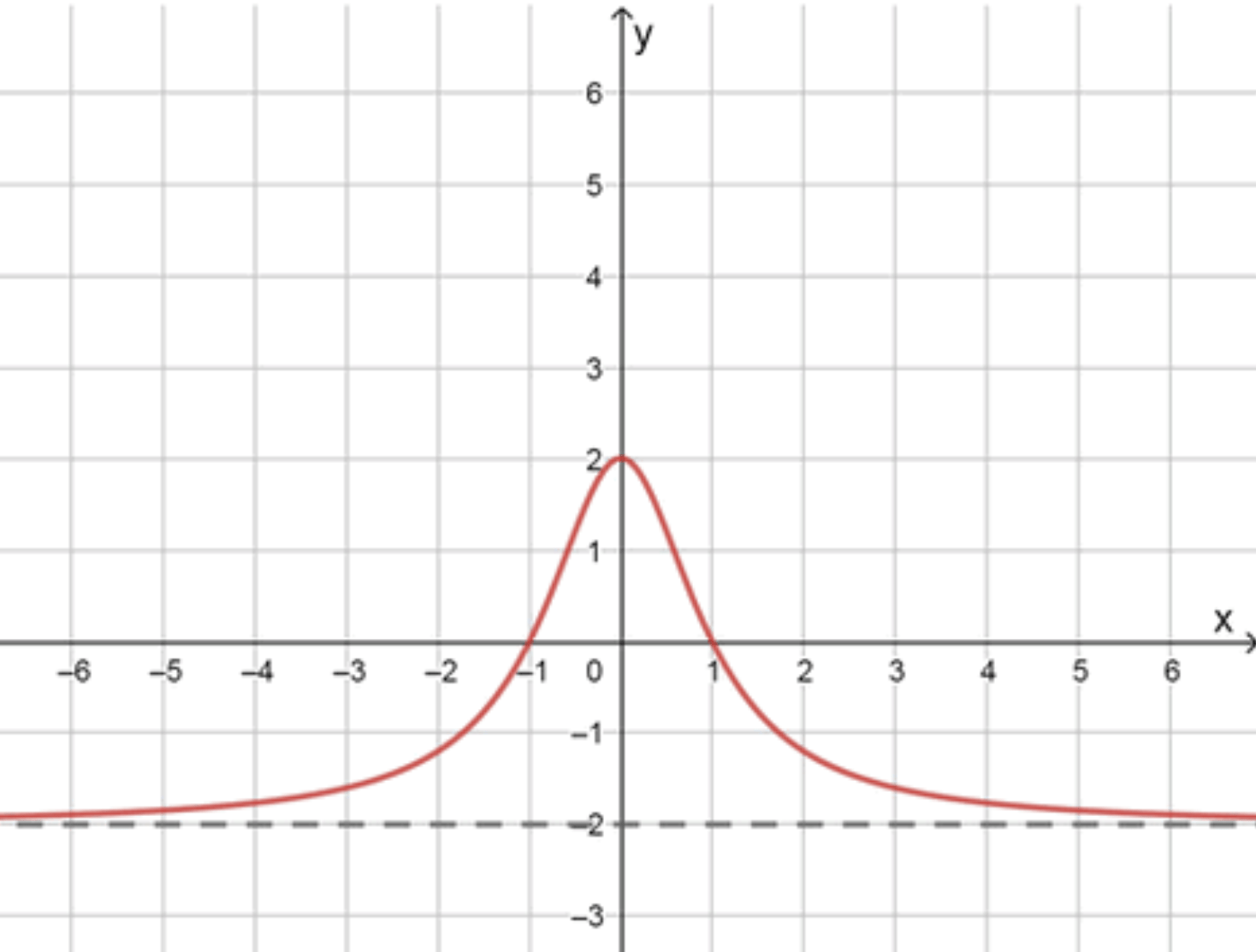
в) $\lim_{x \to +\infty} h(x) = -2$ и функция ограничена

Выбор функции:

$$h(x) = -2 + \frac{\sin x}{x^2 + 1}$$

Почему подходит:

• При $x \to +\infty$, дробь → 0 ⇒ $h(x) \to -2$.
• $\frac{\sin x}{x^2 + 1}$ ограничена по модулю маленьким числом, значит функция ограничена.

Построение:

1. Асимптота: $y = -2$.
2. График — волнистая кривая вокруг –2, амплитуда убывает с ростом $x$.
3. Отметьте несколько точек (например, $x = 0 → 0$, $x=1 → -1.5$, $x=2 → -1.8$).

Как выглядит: волны, сужающиеся к линии $y = -2$ справа.

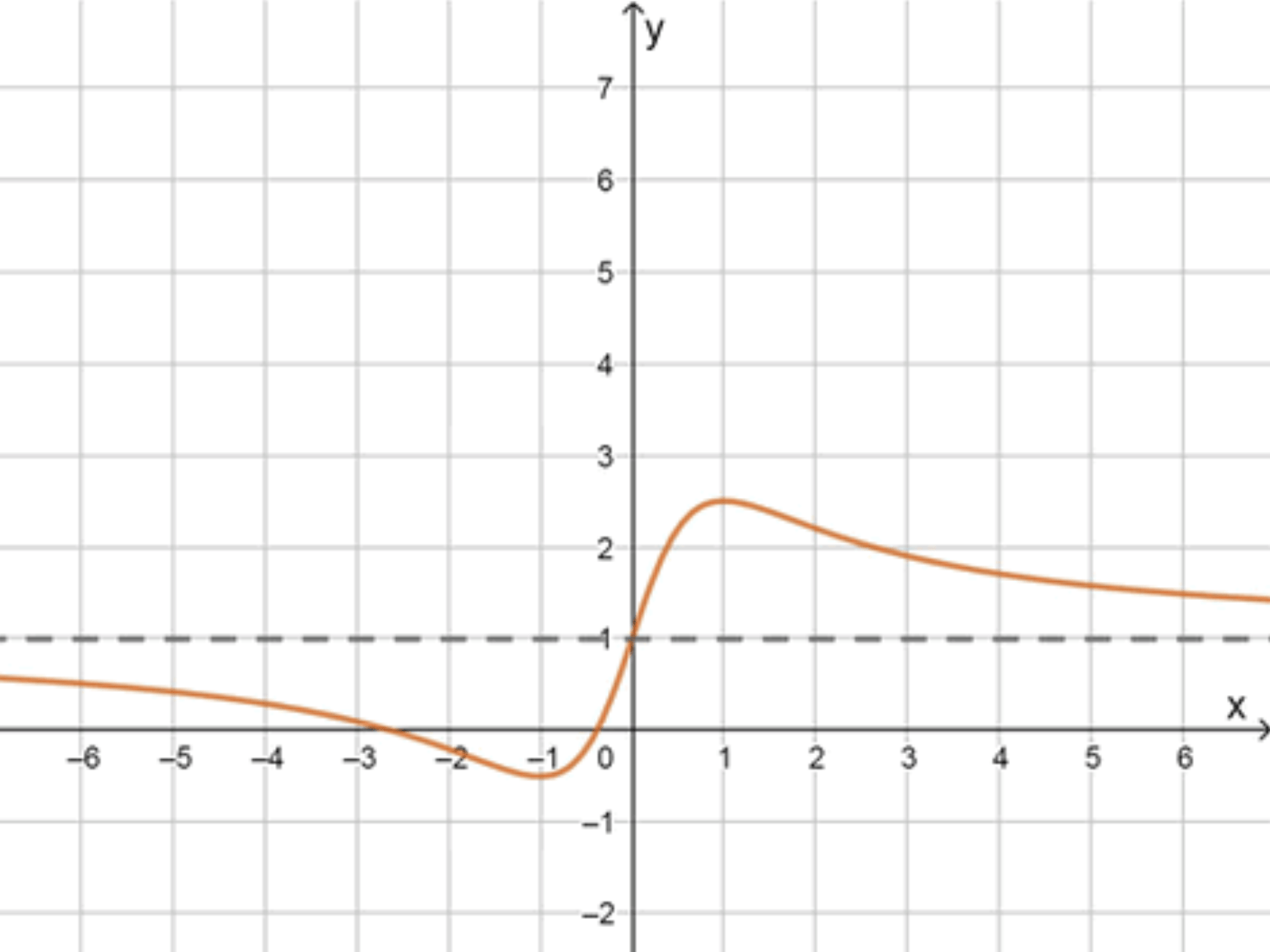
г) $\lim_{x \to +\infty} h(x) = 1$ и функция ограничена

Выбор функции:

$$h(x) = 1 + \frac{\sin x}{2}$$

Почему подходит:

• При $x \to +\infty$, $\sin x$ не имеет предела, но функция ограничена и образует колебания.
• Формально предела нет, но если нужно именно $\to 1$, лучше взять:

$$h(x) = 1 + \frac{\sin x}{x}$$

при котором $\sin x / x \to 0$ ⇒ $h(x) \to 1$.

Построение:

1. Асимптота: $y = 1$.
2. График — затухающая волна вблизи $y = 1$, всегда между $0.5$ и $1.5$.
3. Точки: $x = 0 →$ undefined, выбирайте $x=1,2,3$ с волновым характером.

Как выглядит: синусоида, плавно уменьшающая амплитуду, стремясь к 1.