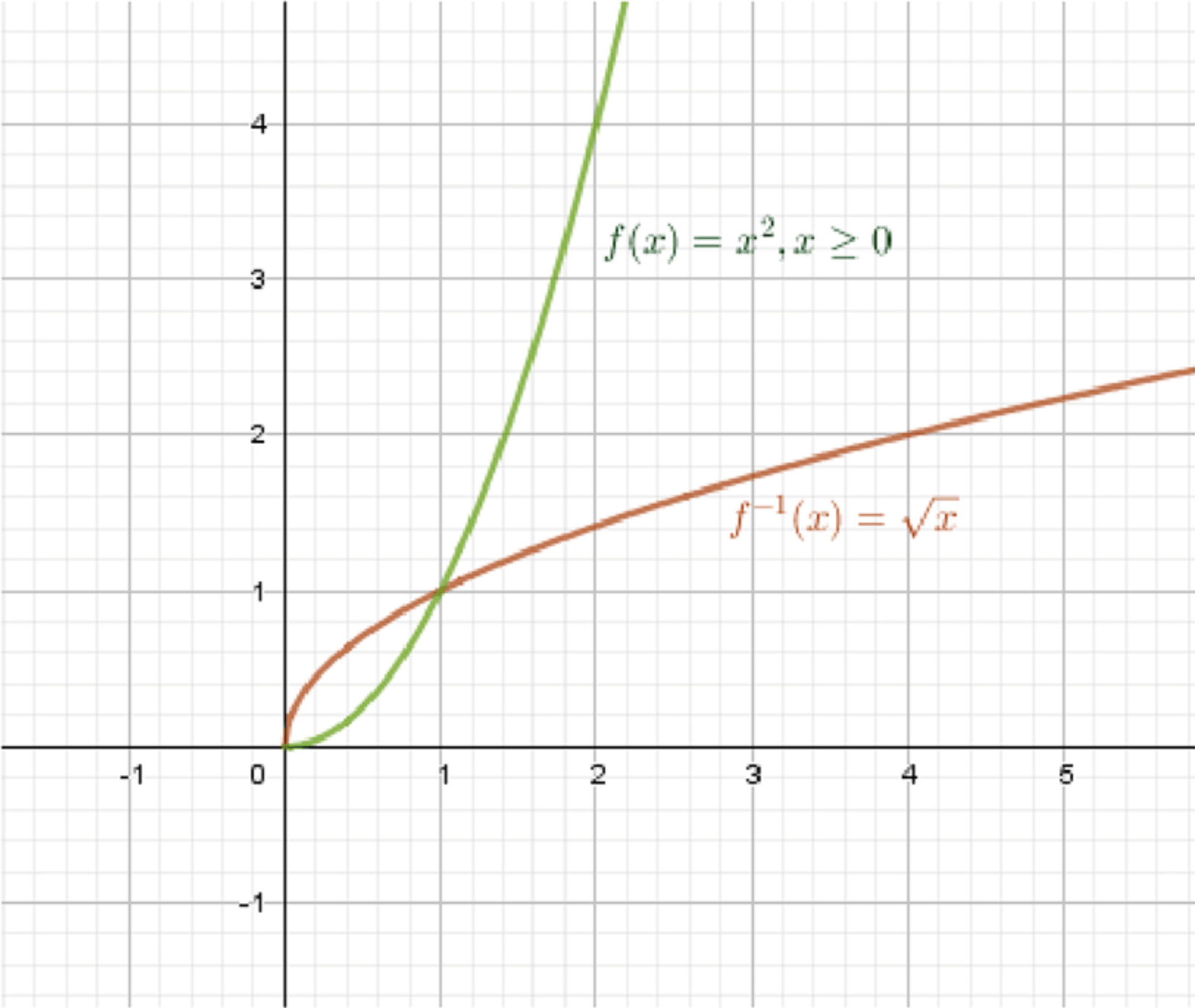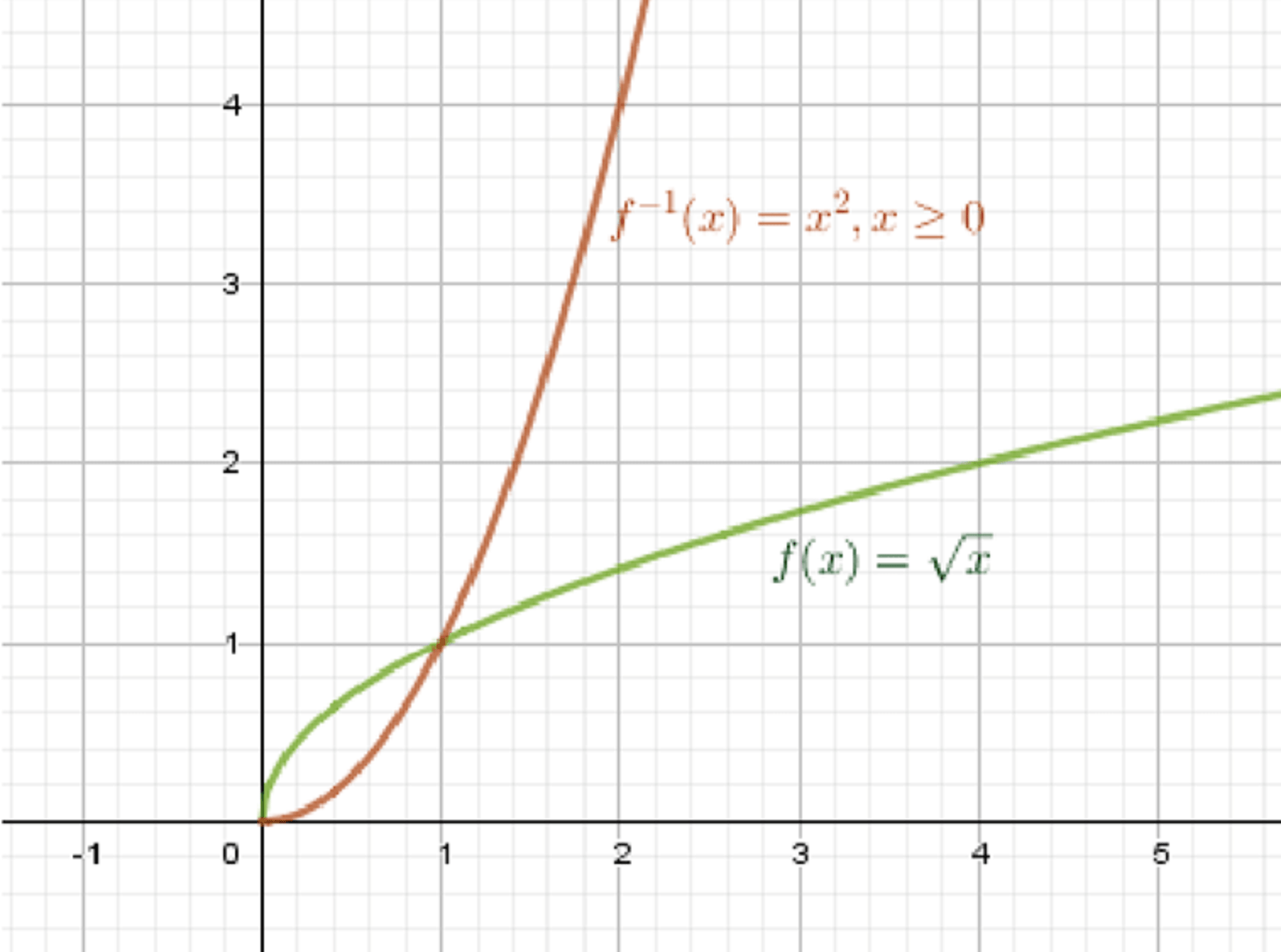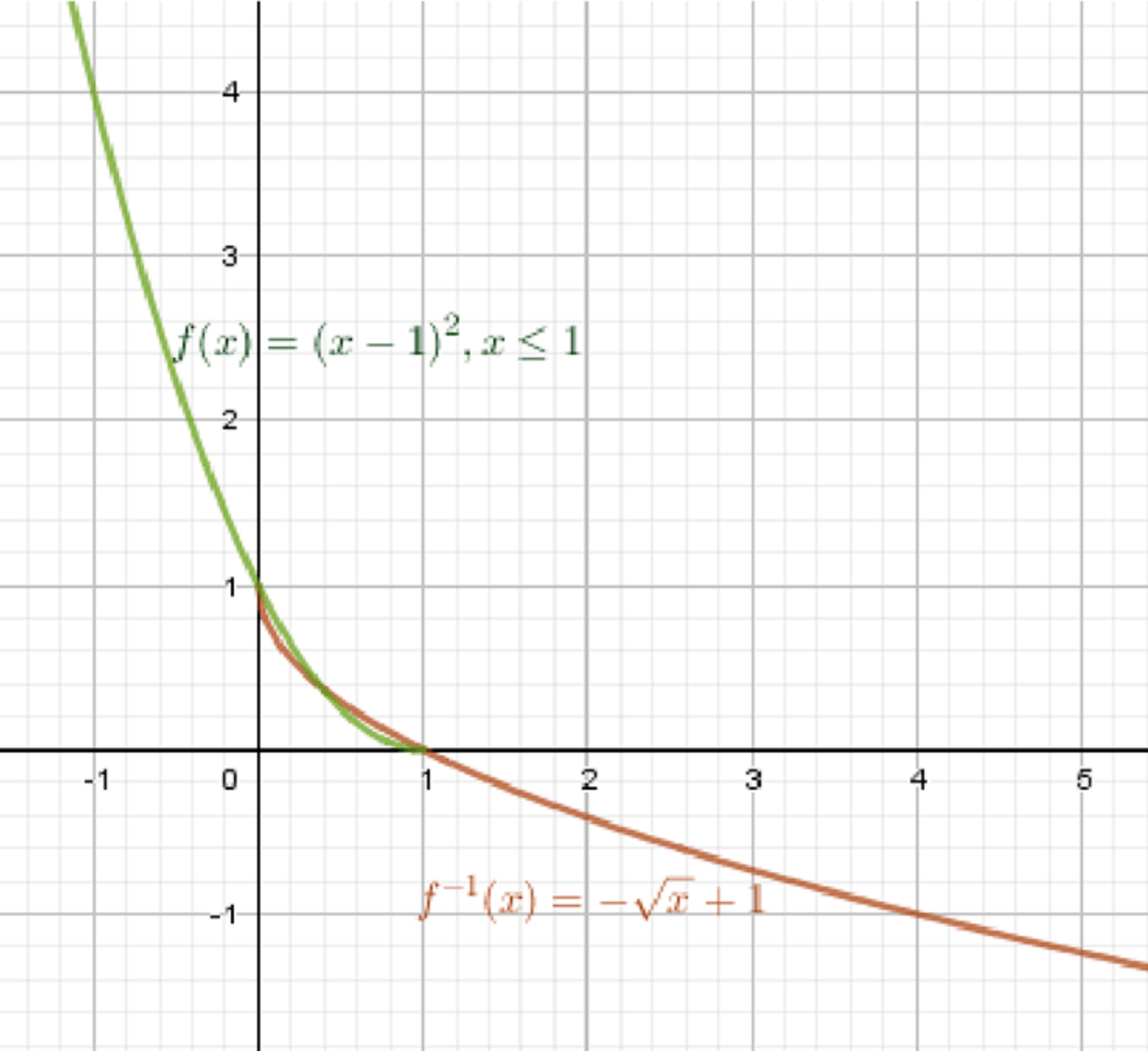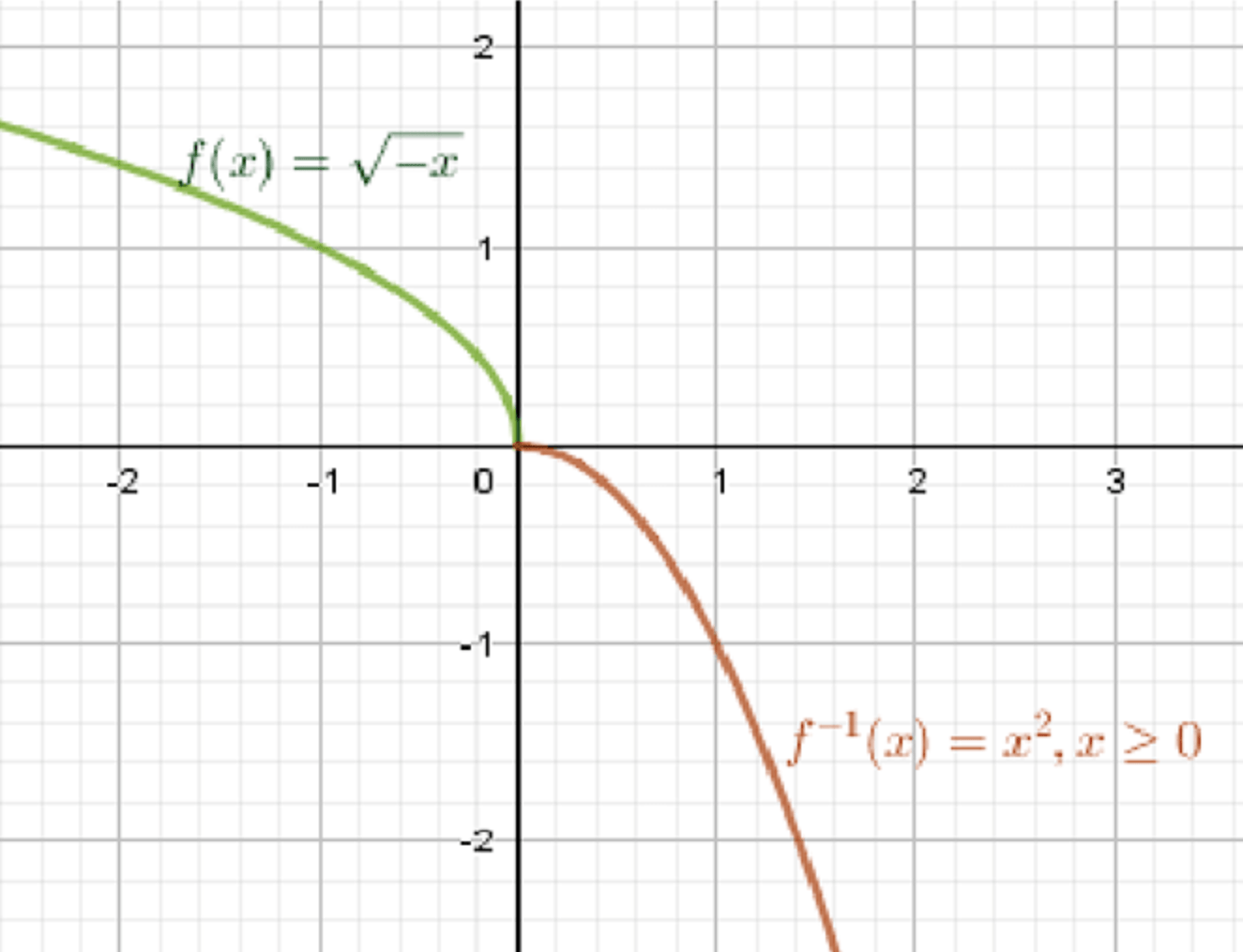ГДЗ 10-11 Класс Номер 3.3 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Для заданной функции найдите обратную; постройте график заданной функции и обратной функции:

а) $y = x^2$, $x \geq 0$;

б) $y = \sqrt{x}$;

в) $y = (x — 1)^2$, $x \leq 1$;

г) $y = \sqrt{-x}$

Для заданной функции найти обратную функцию:

а) $y = x^2$, $x \geq 0$;

Обратная функция:

• $x = y^2$, $y \geq 0$;
• $y = \sqrt{x}$;

Графики функций:

Ответ: $y = \sqrt{x}$.

б) $y = \sqrt{x}$;

Обратная функция:

• $x = \sqrt{y}$, $x \geq 0$;
• $y = x^2$;

Графики функций:

Ответ: $y = x^2$, $x \geq 0$.

в) $y = (x — 1)^2$, $x \leq 1$;

Обратная функция:

• $x = (y — 1)^2$, $y \leq 1$;
• $\sqrt{x} = -(y — 1)$;
• $y = 1 — \sqrt{x}$;

Графики функций:

Ответ: $y = 1 — \sqrt{x}$.

г) $y = \sqrt{-x}$;

Обратная функция:

• $x = \sqrt{-y}$, $x \geq 0$;
• $x^2 = -y$;
• $y = -x^2$;

Графики функций:

Ответ: $y = -x^2$, $x \geq 0$.

а) $y = x^2$, $x \geq 0$

Шаг 1: Преобразование выражения для функции.

Нам дана функция $y = x^2$, при этом $x \geq 0$. Мы должны выразить $x$ через $y$. Для этого нужно решить уравнение $y = x^2$ относительно $x$.

Начнём с того, что извлекаем корень из обеих сторон:

$$\sqrt{y} = \sqrt{x^2}$$

Так как $x \geq 0$ (по условию задачи), то $\sqrt{x^2} = x$. Получаем:

$$x = \sqrt{y}$$

Таким образом, обратная функция:

$$x = \sqrt{y}, \quad y \geq 0$$

или

$$y = \sqrt{x}$$

Шаг 2: Пояснение.

Так как $y = x^2$, то при $x \geq 0$ функция $y$ всегда принимает значения $y \geq 0$. Обратная функция, в свою очередь, имеет вид $y = \sqrt{x}$, поскольку извлечение квадратного корня из $y$ даёт нам положительное значение, соответствующее $x$.

Ответ: $y = \sqrt{x}$, $x \geq 0$.

б) $y = \sqrt{x}$

Шаг 1: Преобразование выражения для функции.

Дана функция $y = \sqrt{x}$. Нам нужно выразить $x$ через $y$.

Для этого возведем обе стороны уравнения в квадрат:

$$y^2 = x$$

Таким образом, обратная функция:

$$x = y^2$$

Шаг 2: Пояснение.

Здесь мы видим, что $y = \sqrt{x}$ представляет собой функцию, которая определена для $x \geq 0$. Обратная функция будет представлять собой $x = y^2$, где $x \geq 0$, так как для $y = \sqrt{x}$ $y$ всегда неотрицательно.

Ответ: $y = x^2$, $x \geq 0$.

в) $y = (x — 1)^2$, $x \leq 1$

Шаг 1: Преобразование выражения для функции.

Дана функция $y = (x — 1)^2$, где $x \leq 1$. Нам нужно выразить $x$ через $y$.

Извлечем квадратный корень из обеих сторон:

$$\sqrt{y} = \sqrt{(x — 1)^2}$$

Так как $x \leq 1$, то $\sqrt{(x — 1)^2} = -(x — 1)$, потому что при $x \leq 1$, выражение $x — 1$ всегда отрицательно или равно нулю.

$$\sqrt{y} = -(x — 1)$$

Перепишем это уравнение, выразив $x$:

$$-(x — 1) = \sqrt{y}$$ $$x — 1 = -\sqrt{y}$$ $$x = 1 — \sqrt{y}$$

Таким образом, обратная функция:

$$x = 1 — \sqrt{y}, \quad y \geq 0$$

Шаг 2: Пояснение.

В данном случае $y = (x — 1)^2$ имеет область определения $x \leq 1$, поэтому извлечение квадратного корня будет давать отрицательную величину, что позволяет нам корректно выразить $x = 1 — \sqrt{y}$.

Ответ: $y = 1 — \sqrt{x}$, $x \geq 0$.

г) $y = \sqrt{-x}$

Шаг 1: Преобразование выражения для функции.

Дана функция $y = \sqrt{-x}$. Нам нужно выразить $x$ через $y$.

Для начала возведем обе стороны уравнения в квадрат:

$$y^2 = -x$$

Теперь выразим $x$:

$$x = -y^2$$

Таким образом, обратная функция:

$$x = -y^2, \quad x \leq 0$$

Шаг 2: Пояснение.

В данном случае $y = \sqrt{-x}$ определена для $x \leq 0$, так как подкоренное выражение $-x$ должно быть неотрицательным. Обратная функция будет иметь вид $x = -y^2$, где $y \geq 0$, так как $y$ всегда неотрицательно для $y = \sqrt{-x}$.

Ответ: $y = -x^2$, $x \geq 0$.

Итоговое решение:

а) $y = x^2$, $x \geq 0$ → Обратная функция: $y = \sqrt{x}$.

б) $y = \sqrt{x}$ → Обратная функция: $y = x^2$, $x \geq 0$.

в) $y = (x — 1)^2$, $x \leq 1$ → Обратная функция: $y = 1 — \sqrt{x}$.

г) $y = \sqrt{-x}$ → Обратная функция: $y = -x^2$, $x \geq 0$.