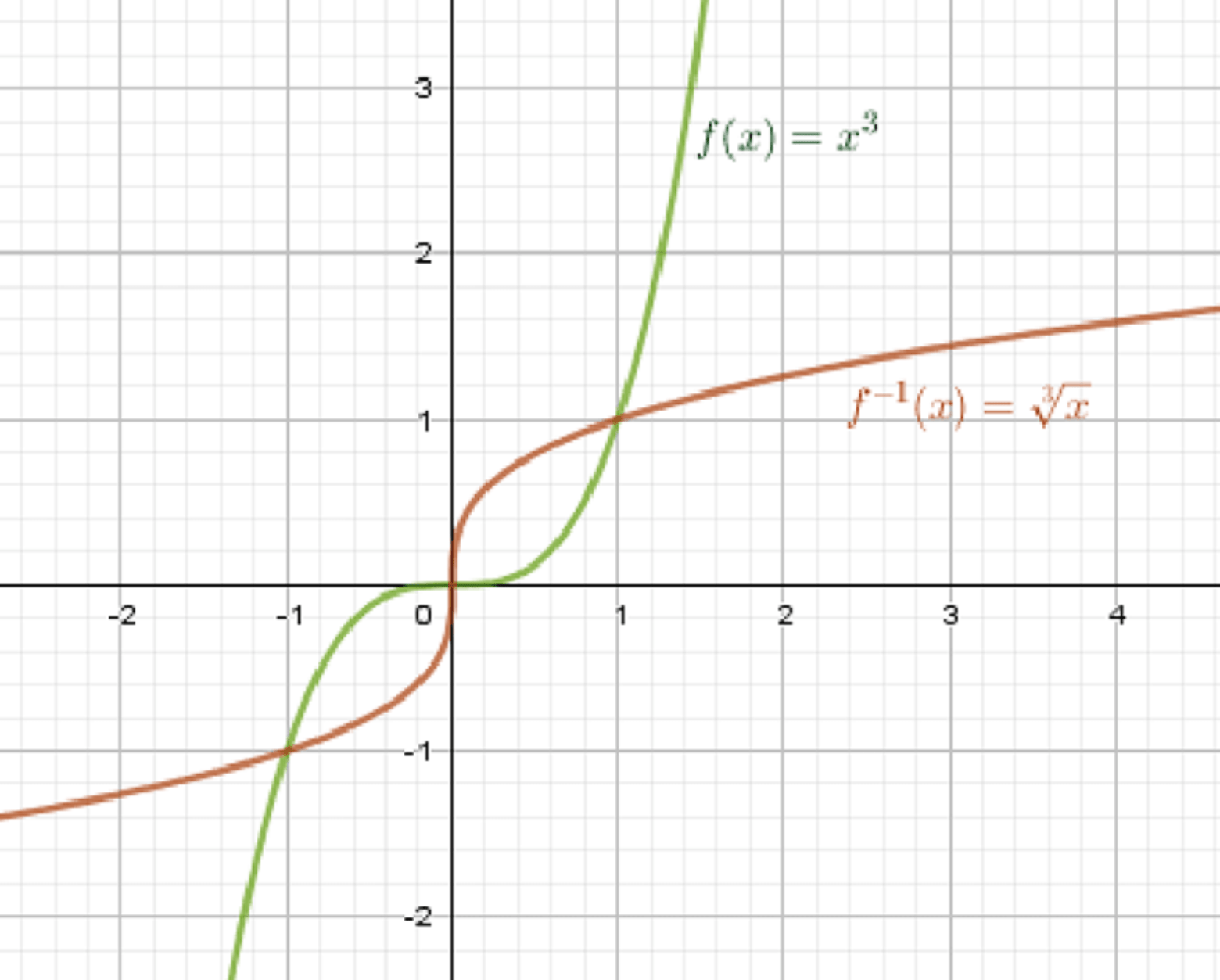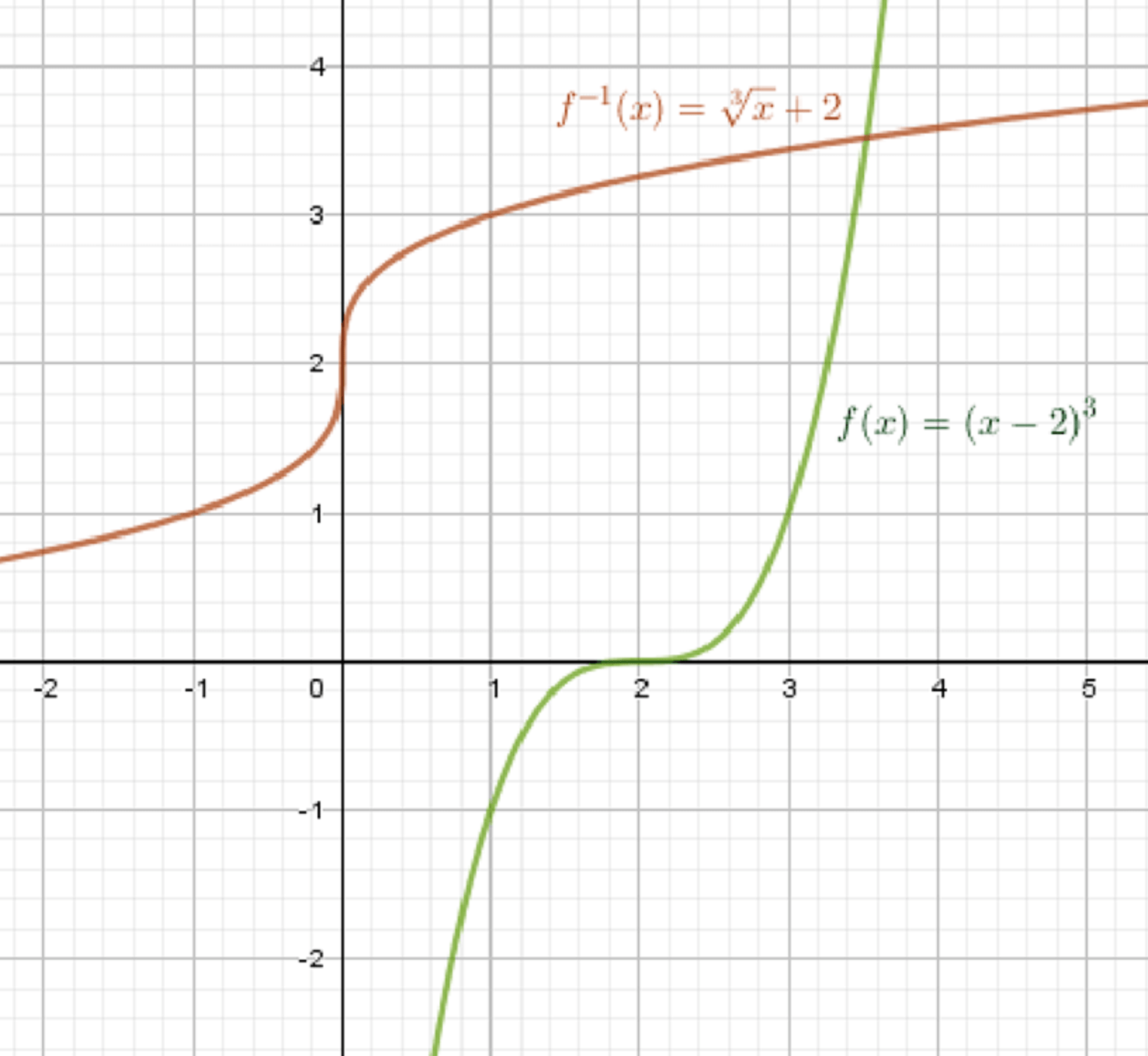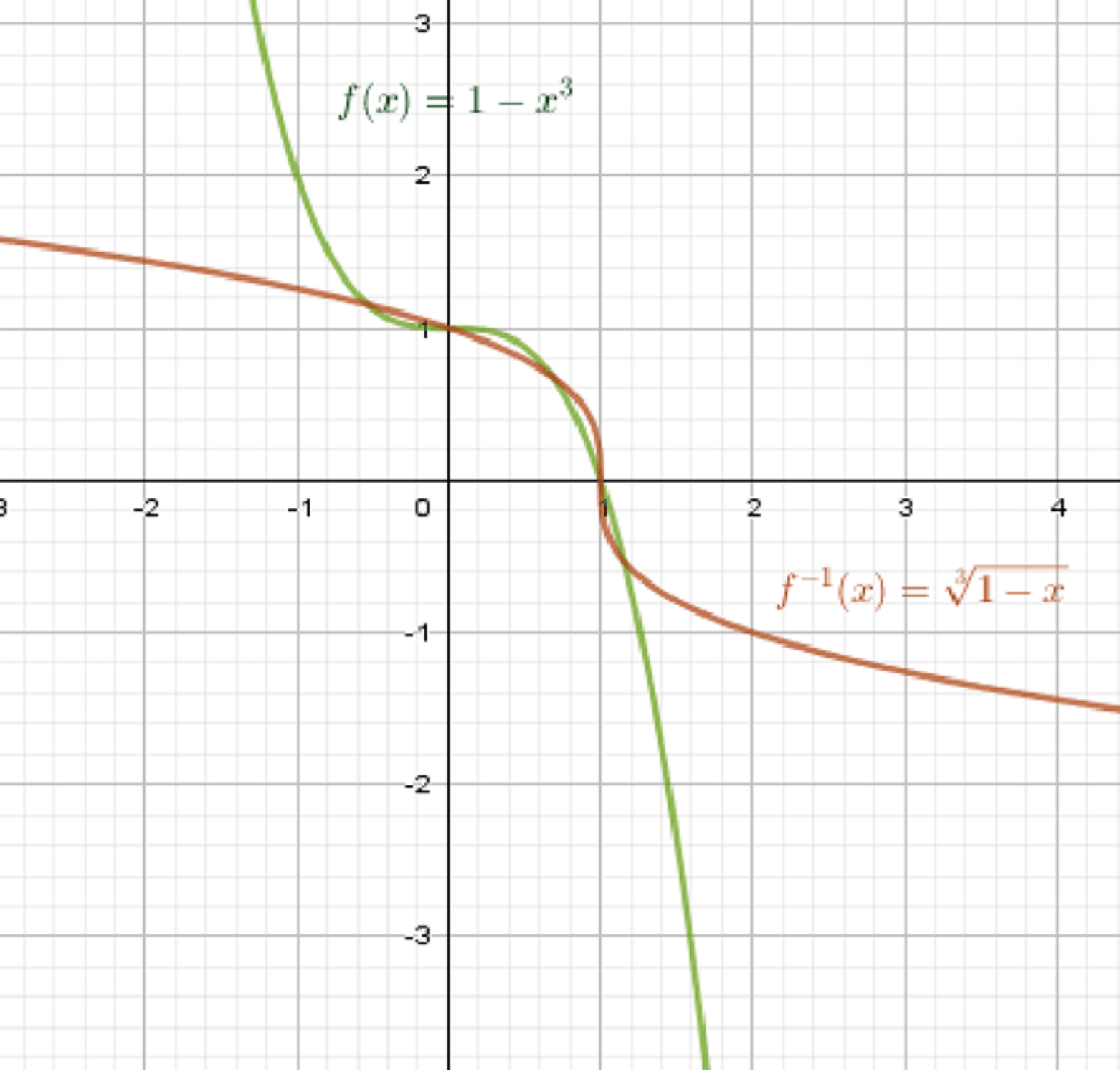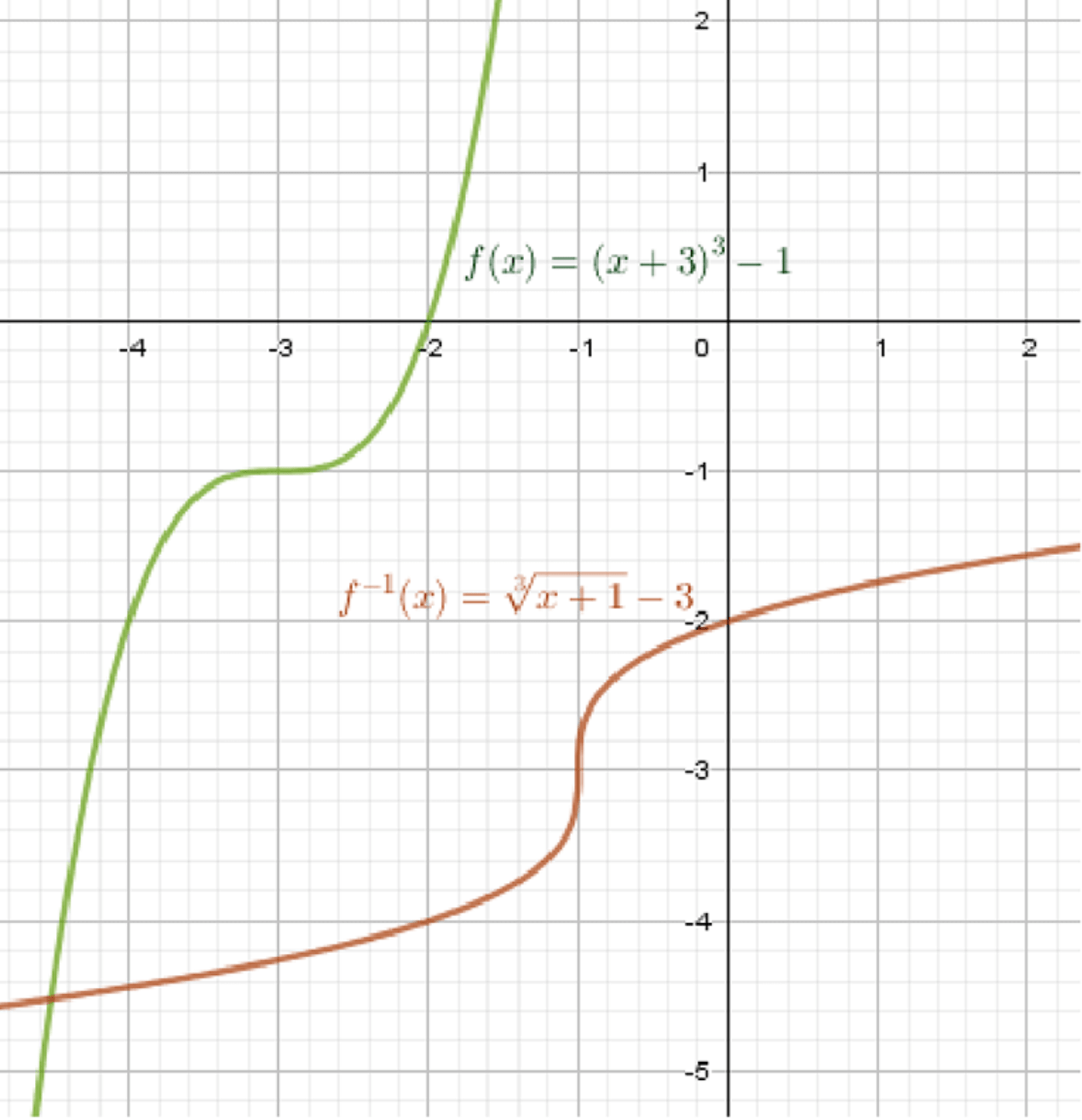ГДЗ 10-11 Класс Номер 3.4 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Для заданной функции найдите обратную; постройте график заданной функции и обратной функции:

а) $y = x^3$;

б) $y = (x — 2)^3$;

в) $y = 1 — x^3$;

г) $y = (x + 3)^3 — 1$

Для заданной функции найти обратную функцию:

а) $y = x^3$;

Обратная функция:

$$x = y^3;$$ $$y = \sqrt[3]{x};$$

Графики функций:

Ответ: $y = \sqrt[3]{x}$.

б) $y = (x — 2)^3$;

Обратная функция:

$$x = (y — 2)^3;$$ $$\sqrt[3]{x} = y — 2;$$ $$y = \sqrt[3]{x} + 2;$$

Графики функций:

Ответ: $y = \sqrt[3]{x} + 2$.

в) $y = 1 — x^3$;

Обратная функция:

$$x = 1 — y^3;$$ $$y^3 = 1 — x;$$ $$y = \sqrt[3]{1 — x};$$

Графики функций:

Ответ: $y = \sqrt[3]{1 — x}$.

г) $y = (x + 3)^3 — 1$;

Обратная функция:

$$x = (y + 3)^3 — 1;$$ $$(y + 3)^3 = x + 1;$$ $$y + 3 = \sqrt[3]{x + 1};$$ $$y = \sqrt[3]{x + 1} — 3;$$

Графики функций:

Ответ: $y = \sqrt[3]{x + 1} — 3$.

Обратная функция для функции $y = f(x)$ — это функция $x = f^{-1}(y)$, которая «меняет местами» переменные $x$ и $y$. То есть для нахождения обратной функции нужно выразить $x$ через $y$ и затем решить для $y$.

а) $y = x^3$

Исходная функция:

$$y = x^3$$

Поменяем местами $x$ и $y$:
Чтобы найти обратную функцию, меняем местами $x$ и $y$. Получаем:

$$x = y^3$$

Решим это уравнение для $y$:
Чтобы выразить $y$ через $x$, нужно извлечь кубический корень из обеих сторон:

$$y = \sqrt[3]{x}$$

Ответ:
Таким образом, обратная функция:

$$y = \sqrt[3]{x}$$

График:

б) $y = (x — 2)^3$

Исходная функция:

$$y = (x — 2)^3$$

Поменяем местами $x$ и $y$:
Меняем местами $x$ и $y$:

$$x = (y — 2)^3$$

Решим это уравнение для $y$:
Чтобы выразить $y$, сначала извлечем кубический корень из обеих сторон:

$$\sqrt[3]{x} = y — 2$$

Теперь, чтобы изолировать $y$, добавим 2 к обеим частям уравнения:

$$y = \sqrt[3]{x} + 2$$

Ответ:
Обратная функция:

$$y = \sqrt[3]{x} + 2$$

График:

в) $y = 1 — x^3$

Исходная функция:

$$y = 1 — x^3$$

Поменяем местами $x$ и $y$:
Меняем местами $x$ и $y$:

$$x = 1 — y^3$$

Решим это уравнение для $y$:
Чтобы выразить $y$, сначала переместим $1$ на другую сторону:

$$y^3 = 1 — x$$

Теперь извлечем кубический корень из обеих сторон:

$$y = \sqrt[3]{1 — x}$$

Ответ:
Обратная функция:

$$y = \sqrt[3]{1 — x}$$

График:

г) $y = (x + 3)^3 — 1$

Исходная функция:

$$y = (x + 3)^3 — 1$$

Поменяем местами $x$ и $y$:
Меняем местами $x$ и $y$:

$$x = (y + 3)^3 — 1$$

Решим это уравнение для $y$:
Переносим $-1$ на правую сторону:

$$(y + 3)^3 = x + 1$$

Теперь извлекаем кубический корень из обеих сторон:

$$y + 3 = \sqrt[3]{x + 1}$$

Чтобы изолировать $y$, вычитаем 3 с обеих сторон:

$$y = \sqrt[3]{x + 1} — 3$$

Ответ:
Обратная функция:

$$y = \sqrt[3]{x + 1} — 3$$

График: