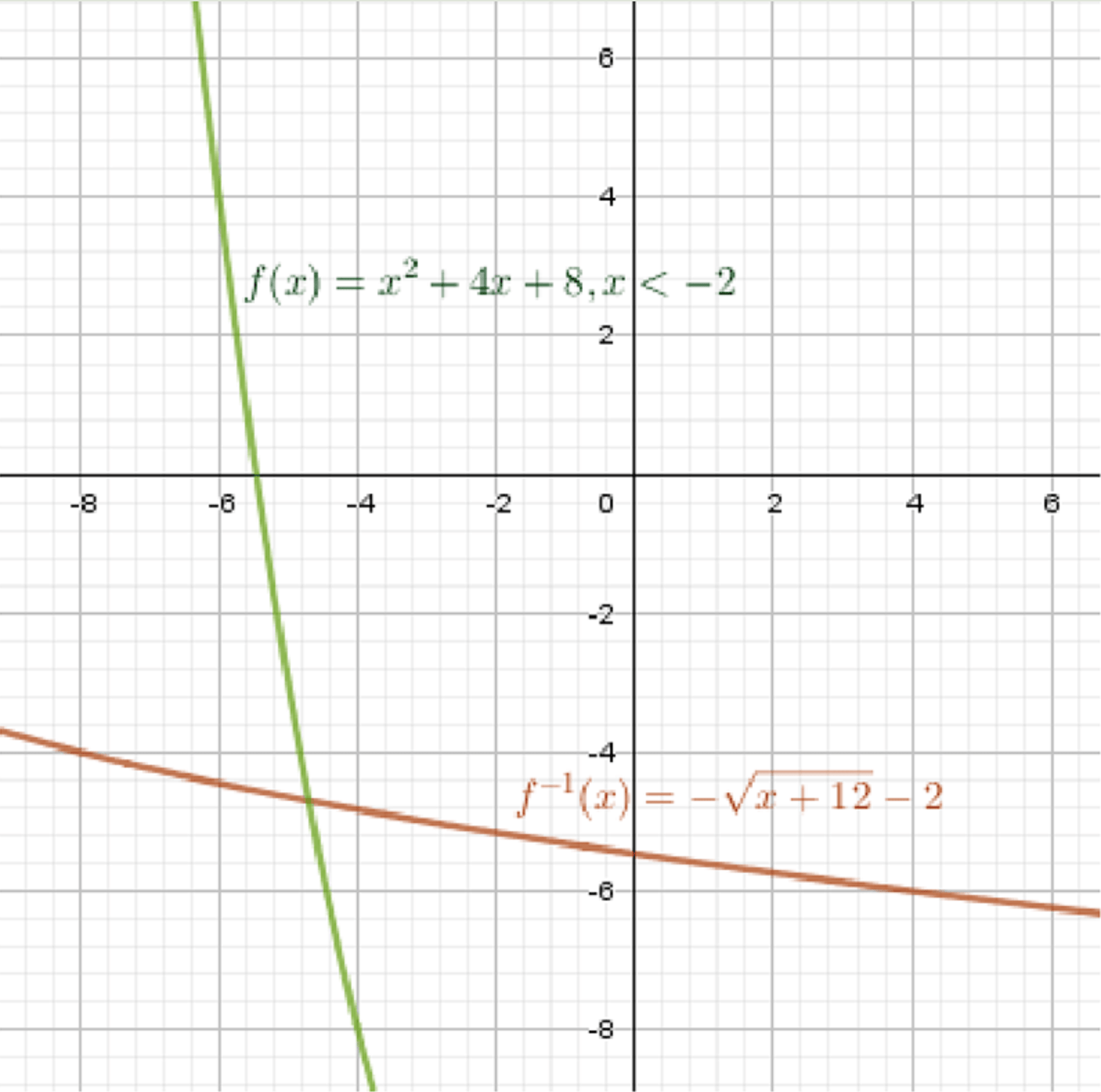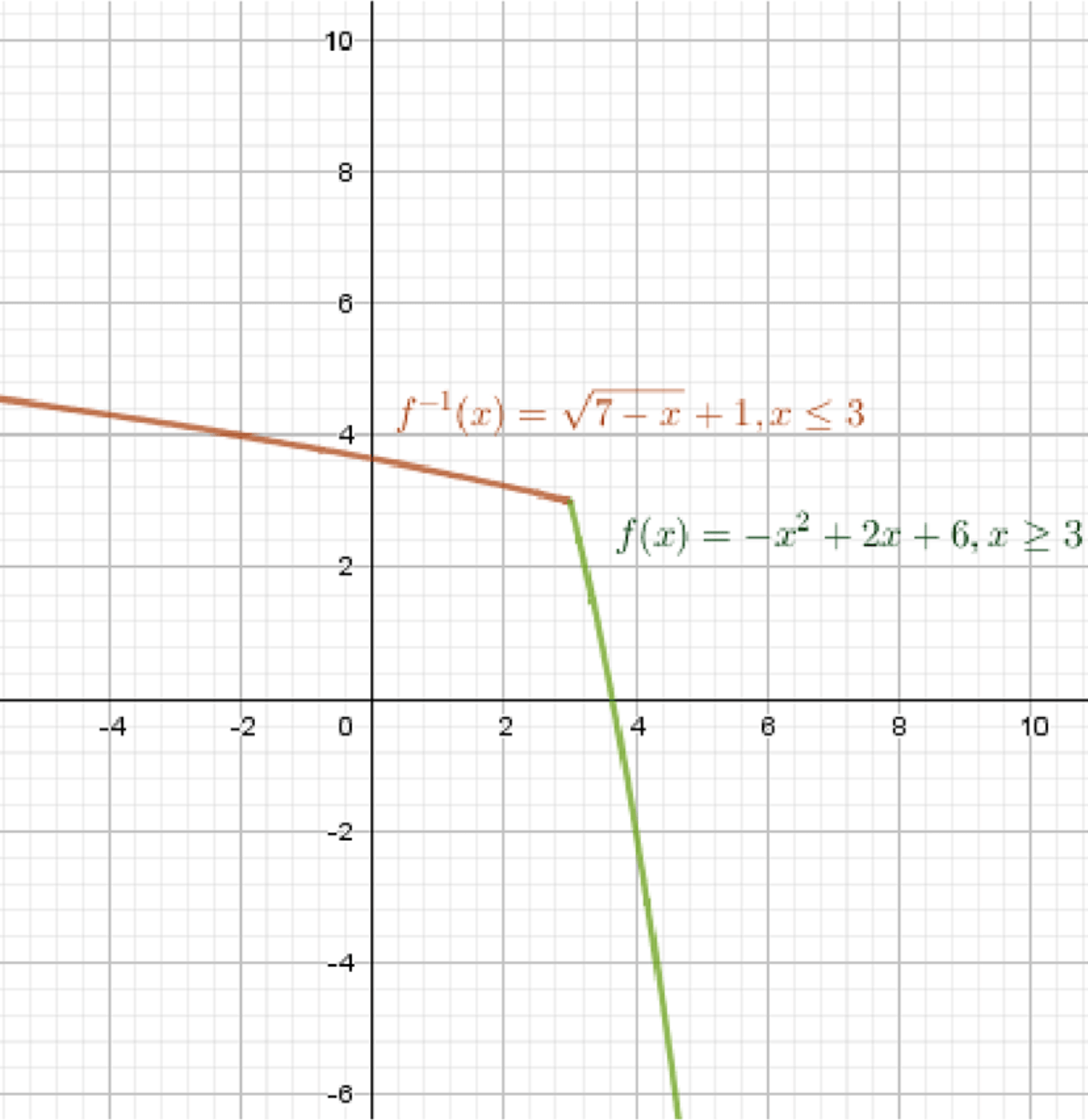ГДЗ 10-11 Класс Номер 3.5 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Выясните, существует ли обратная функция для заданной функции. Если да, то задайте обратную функцию аналитически, постройте график заданной и обратной функций:

а) $y = x^2 + 4x — 8$, $x \in [-3; 0]$

б) $y = x^2 + 4x — 8$, $x \in (-\infty; -2)$

в) $y = -x^2 + 2x + 6$, $x \in [0; 3]$

г) $y = -x^2 + 2x + 6$, $x\in [3;+\mathrm{\infty })$

Выяснить, существует ли обратная функция:

а) $y = x^2 + 4x — 8$, $x \in [-3; 0]$

Абсцисса вершины параболы:

$$x_0 = -\frac{b}{2a} = -\frac{4}{2 \cdot 1} = -2$$

Ответ: не существует.

б) $y = x^2 + 4x — 8$, $x \in (-\infty; -2)$

Координаты вершины параболы:

$$x_0 = -\frac{b}{2a} = -\frac{4}{2 \cdot 1} = -2$$ $$y_0 = 4 — 8 — 8 = -12$$

Координаты некоторых точек:

$$\begin{array}{c|ccc} x & -5 & -4 & -3 \\ \hline y & -3 & -8 & -11 \\ \end{array}$$

Обратная функция:

$$x = y^2 + 4y — 8, \quad y < -2$$ $$x = (y + 2)^2 — 12$$ $$(y + 2)^2 = x + 12$$ $$-(y + 2) = \sqrt{x + 12}$$ $$y = -\sqrt{x + 12} — 2$$

Графики функций:

Ответ: $y = -\sqrt{x + 12} — 2$.

в) $y = -x^2 + 2x + 6$, $x \in [0; 3]$

Абсцисса вершины параболы:

$$x_0 = -\frac{b}{2a} = -\frac{2}{2 \cdot (-1)} = 1$$

Ответ: не существует.

г) $y = -x^2 + 2x + 6$, $x \in [3; +\infty)$

Координаты вершины параболы:

$$x_0 = -\frac{b}{2a} = -\frac{2}{2 \cdot (-1)} = 1$$ $$y_0 = -1 + 2 + 6 = 7$$

Координаты некоторых точек:

$$\begin{array}{c|ccc} x & 3 & 4 & 5 \\ \hline y & 3 & -2 & -9 \\ \end{array}$$

Обратная функция:

$$x = -y^2 + 2y + 6, \quad y \geq 3$$ $$x = -(y — 1)^2 + 7$$ $$(y — 1)^2 = 7 — x$$ $$y — 1 = \sqrt{7 — x}$$ $$y = \sqrt{7 — x} + 1$$

Область определения:

$$\sqrt{7 — x} + 1 \geq 3$$ $$\sqrt{7 — x} \geq 2$$ $$7 — x \geq 4$$ $$x \leq 3$$

Графики функций:

Ответ: $y = \sqrt{7 — x} + 1$, $x \leq 3$.

Заметка: Обратная функция существует только тогда, когда функция является инъективной, то есть при каждом значении $y$ существует только одно значение $x$. Для функций, заданных через параболы или другие многочлены второй степени, нужно быть внимательными, потому что такие функции могут быть неинъективными на всем своем определении. Иногда для существования обратной функции требуется ограничить область определения.

а) $y = x^2 + 4x — 8$, $x \in [-3; 0]$

Исходная функция:

$$y = x^2 + 4x — 8$$

Это квадратичная функция, которая представляет собой параболу.

Проверка инъективности:
Чтобы выяснить, существует ли обратная функция, нужно проверить, является ли эта функция инъективной на заданной области $x \in [-3; 0]$.

Парабола может быть неинъективной, так как она может принимать одно и то же значение $y$ для разных значений $x$. Однако если мы ограничим область определения, то функция станет инъективной на этом промежутке.

Но перед этим давайте найдем вершину параболы, чтобы убедиться, что функция на данной области действительно инъективна.

Абсцисса вершины параболы:
Вершина параболы для квадратичной функции $y = ax^2 + bx + c$ находится в точке:

$$x_0 = -\frac{b}{2a}$$

Здесь $a = 1$, $b = 4$, и $c = -8$. Подставляем:

$$x_0 = -\frac{4}{2 \cdot 1} = -2$$

Вершина параболы находится в точке $x = -2$, которая лежит внутри рассматриваемого промежутка $[-3; 0]$.

Ответ:
Так как вершина параболы лежит внутри промежутка $[-3; 0]$, и функция на этом промежутке принимает разные значения для разных $x$, она не является инъективной на этом интервале. Следовательно, обратная функция не существует.

Ответ: не существует.

б) $y = x^2 + 4x — 8$, $x \in (-\infty; -2)$

Исходная функция:

$$y = x^2 + 4x — 8$$

Это та же самая квадратичная функция, но теперь область определения ограничена интервалом $x \in (-\infty; -2)$.

Проверка инъективности:
Мы снова имеем параболу, но с ограниченной областью определения. Парабола будет инъективной, если она монотонна (то есть либо возрастает, либо убывает) на рассматриваемом интервале.

Абсцисса вершины параболы:
Мы уже знаем, что абсцисса вершины параболы:

$$x_0 = -2$$

Вершина находится на границе интервала, следовательно, на интервале $(-\infty; -2)$ функция будет монотонно убывать.

Координаты вершины параболы:
Подставляем $x_0 = -2$ в исходную функцию:

$$y_0 = (-2)^2 + 4(-2) — 8 = 4 — 8 — 8 = -12$$

Таким образом, вершина параболы имеет координаты $(-2, -12)$.

Координаты некоторых точек:
Подставим несколько значений $x$ из интервала $(-\infty; -2)$, чтобы вычислить соответствующие значения $y$:

$$\begin{array}{c|ccc} x & -5 & -4 & -3 \\ \hline y & -3 & -8 & -11 \\ \end{array}$$

Мы видим, что значения $y$ разные для разных значений $x$, что подтверждает, что функция инъективна на этом интервале.

Нахождение обратной функции:
Поменяем местами $x$ и $y$ в исходной функции:

$$x = y^2 + 4y — 8$$

Решим это уравнение для $y$:

$$x + 8 = y^2 + 4y$$ $$x + 8 = (y + 2)^2 — 12$$ $$(y + 2)^2 = x + 12$$

Извлекаем квадратный корень:

$$-(y + 2) = \sqrt{x + 12}$$ $$y = -\sqrt{x + 12} — 2$$

Ответ:
Таким образом, обратная функция:

$$y = -\sqrt{x + 12} — 2$$

в) $y = -x^2 + 2x + 6$, $x \in [0; 3]$

Исходная функция:

$$y = -x^2 + 2x + 6$$

Это снова квадратичная функция, представляющая собой параболу, но с другим направлением ветвей (она открывается вниз, так как коэффициент при $x^2$ отрицателен).

Проверка инъективности:
Для того чтобы функция была инъективной, она должна быть монотонной на рассматриваемом промежутке. Проверим, является ли функция монотонной.

Абсцисса вершины параболы:

$$x_0 = -\frac{b}{2a} = -\frac{2}{2 \cdot (-1)} = 1$$

Вершина параболы находится в точке $x = 1$, которая лежит внутри интервала $[0; 3]$.

Ответ:
Функция не является инъективной на интервале $[0; 3]$, так как она не монотонна (она сначала возрастает, а затем убывает). Следовательно, обратная функция не существует.

Ответ: не существует.

г) $y = -x^2 + 2x + 6$, $x \in [3; +\infty)$

Исходная функция:

$$y = -x^2 + 2x + 6$$

Парабола открывается вниз, но теперь область определения ограничена интервалом $[3; +\infty)$.

Проверка инъективности:
На интервале $[3; +\infty)$ функция будет монотонно убывать, потому что после вершины парабола начинает уменьшаться. Следовательно, функция инъективна на этом интервале.

Абсцисса вершины параболы:

$$x_0 = -\frac{b}{2a} = -\frac{2}{2 \cdot (-1)} = 1$$

Вершина находится в точке $x = 1$, но поскольку $x \geq 3$, функция монотонно убывает и инъективна.

Координаты вершины параболы:
Подставляем $x_0 = 1$ в исходную функцию:

$$y_0 = -(1)^2 + 2(1) + 6 = 7$$

Вершина параболы имеет координаты $(1, 7)$.

Координаты некоторых точек:
Подставим несколько значений $x$ из интервала $[3; +\infty)$:

$$\begin{array}{c|ccc} x & 3 & 4 & 5 \\ \hline y & 3 & -2 & -9 \\ \end{array}$$

Нахождение обратной функции:
Поменяем местами $x$ и $y$:

$$x = -y^2 + 2y + 6$$

Решим для $y$:

$$x = -(y — 1)^2 + 7$$ $$(y — 1)^2 = 7 — x$$ $$y — 1 = \sqrt{7 — x}$$ $$y = \sqrt{7 — x} + 1$$

Область определения:
Функция должна быть определена для всех $x \leq 3$, потому что извлекаемый корень из $7 — x$ должен быть действительным.

Ответ:
Обратная функция:

$$y=\sqrt{7-x}+1,x\le 3$$