ГДЗ 10-11 Класс Номер 30.33 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

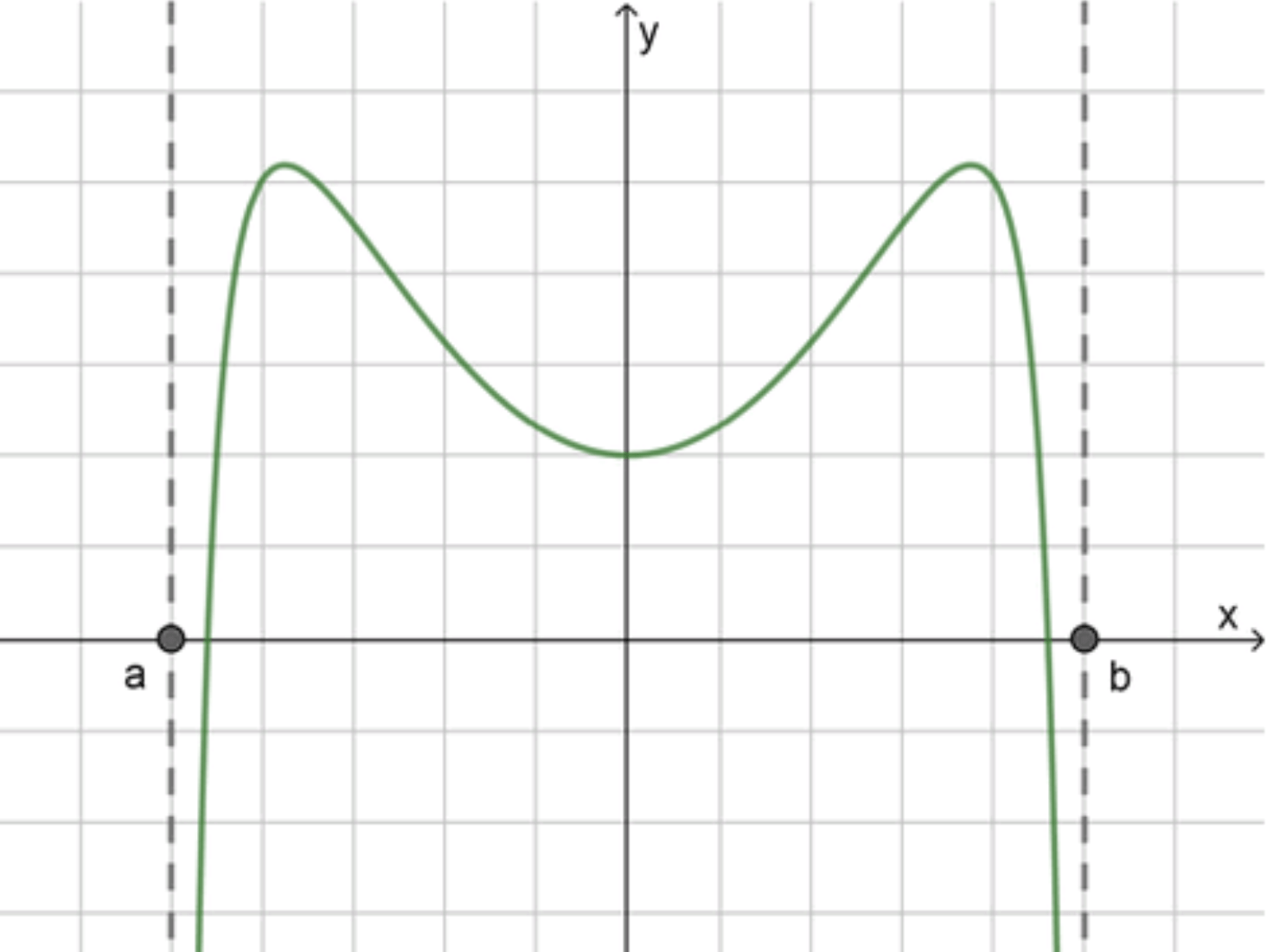
а) Постройте эскиз графика функции, дифференцируемой на интервале (а; Ь), имеющей на этом интервале одну точку минимума, две точки максимума и не имеющей наименьшего значения.

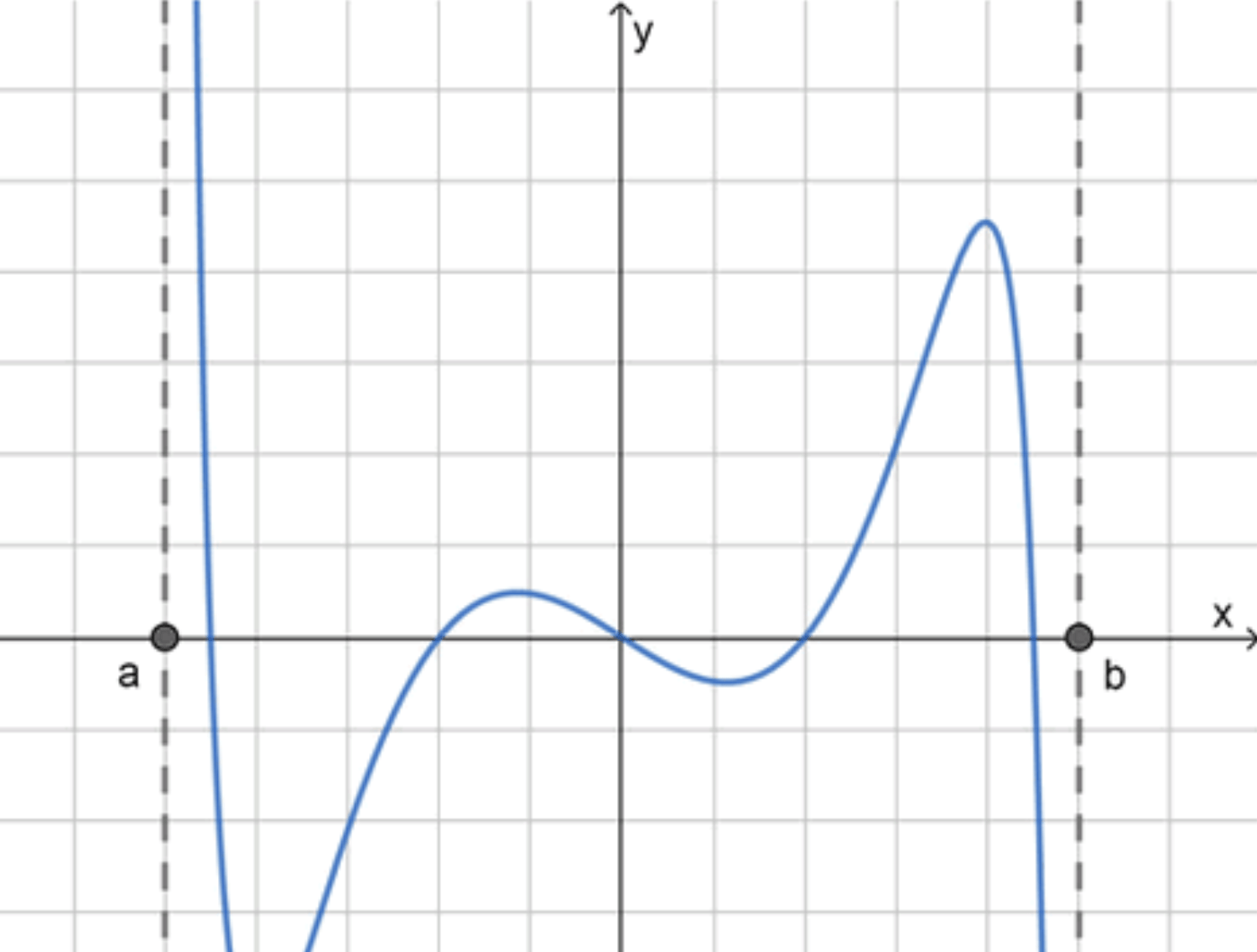
б) Постройте эскиз графика функции, дифференцируемой на интервале (а; b), имеющей на нём две точки минимума, две точки максимума, но не имеющей ни наименьшего, ни наибольшего значений.

Построить эскиз графика функции, дифференцируемой на интервале (a; b) и обладающей указанными свойствами:

а) Функция на заданном интервале:
– Имеет одну точку минимума и две точки максимума;
– Не имеет наименьшего значения;

б) Функция на заданном интервале:
– Имеет две точки минимума и две точки максимума;
– Не имеет ни наименьшего, ни наибольшего значений;

Функция:

• Дифференцируема на интервале $(a; b)$ → значит:
  • График гладкий (без разрывов и углов),
  • В каждой точке есть касательная (первая производная существует).

Эскиз:

• Не требуется точный вид функции, но важна форма графика: где максимум, минимум, возрастание/убывание и поведение на концах.

Задание а)

Условия:

1. Имеет одну точку минимума и две точки максимума;
2. Не имеет наименьшего значения.

Шаг 1. Что означает «одна точка минимума и две точки максимума»?

• Три экстремальные точки:
  • Первая – максимум,
  • Вторая – минимум,
  • Третья – максимум.

Шаг 2. «Не имеет наименьшего значения»

• Значит: функция уходит вниз бесконечно, т.е.

  $$\lim_{x \to a^+} f(x) = -\infty \quad \text{или} \quad \lim_{x \to b^-} f(x) = -\infty$$

• То есть, нет самой «низкой точки» — функция спускается вниз без ограничения.

Как выглядит график?

• Представь интервал $(a; b)$, например, от $x = -5$ до $x = 5$.
• Построение:

Геометрически:

• Форма: горка – впадина – горка – спад (вниз бесконечно).
• У функции:
  • 2 точки максимума (две вершины),
  • 1 точка минимума (одна впадина),
  • Конец графика уходит вниз → нет нижней границы.

Задание б)

Условия:

1. Имеет две точки минимума и две точки максимума;
2. Не имеет ни наименьшего, ни наибольшего значений.

Шаг 1. Что означает «две точки минимума и две точки максимума»?

• Чередование: максимум – минимум – максимум – минимум.

→ Значит, 4 экстремума, а график петляет.

Шаг 2. «Не имеет ни наименьшего, ни наибольшего значений»

• Значит: функция уходит в бесконечность и вниз бесконечно, т.е.
  • $\lim_{x \to a^+} f(x) = -\infty$
  • $\lim_{x \to b^-} f(x) = +\infty$
  • (или наоборот)

Как выглядит график?

• Выбираем интервал $(a; b)$, например от $x = -5$ до $x = 5$
• Построение:

• Таким образом:
  • 2 максимума — две «вершины»,
  • 2 минимума — две «впадины»,
  • Функция не ограничена сверху и снизу — крайние участки графика стремятся к бесконечности.