ГДЗ 10-11 Класс Номер 30.35 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте эскиз графика какой-нибудь функции, обладающей указанными свойствами:

а) функция имеет две точки максимума, одну точку минимума и является ограниченной;

б) функция возрастает при $x \leq 1$ и $x\ge 5$ и убывает на промежутке [1; 5]; точка х = 1 является критической, а точка х = 5 — стационарной;

в) функция имеет разрыв в точке х = -2, максимум в точке x = -1 и минимум в точке х = 1;

г) функция имеет горизонтальную асимптоту $y = 3$ при $x\to \mathrm{\infty }$, одну точку максимума и одну точку минимума.

Построить эскиз графика какой-нибудь функции, обладающей указанными свойствами:

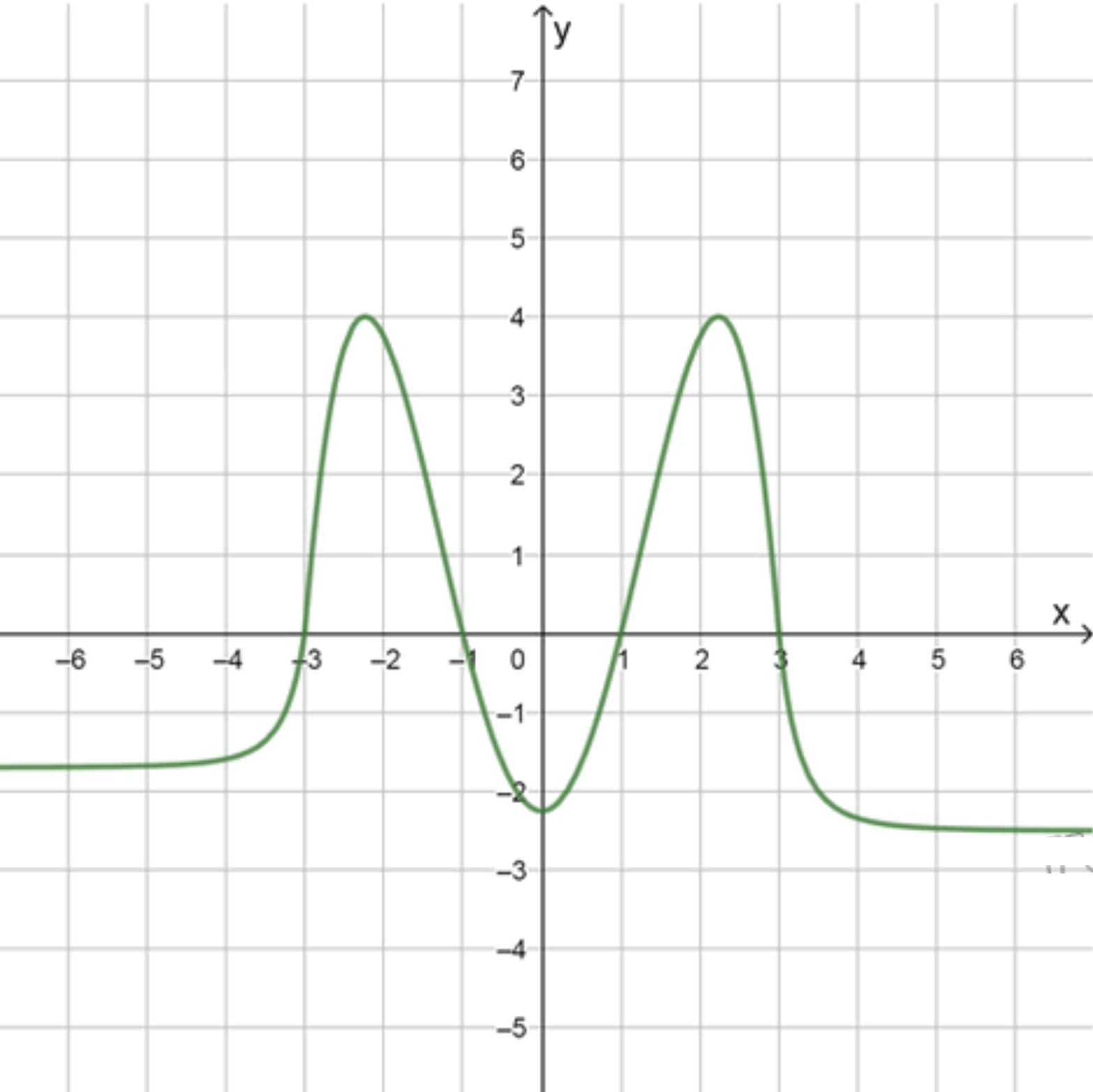
а) Функция имеет две точки максимума, одну точку минимума и является ограниченной:

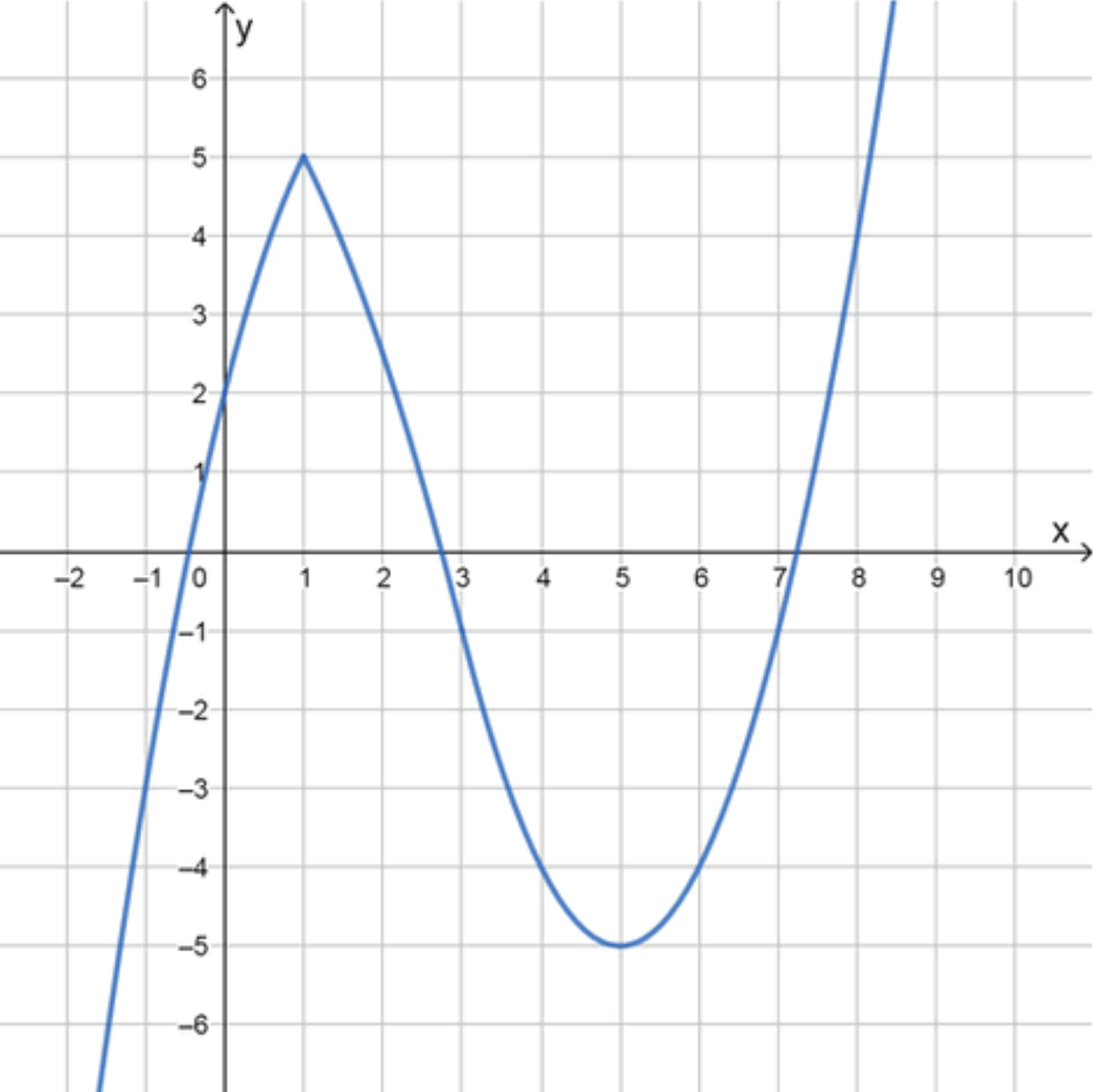
б) Функция возрастает при $x \leq 1$ и $x \geq 5$ и убывает на промежутке $[1; 5]$; точка $x = 1$ является критической, а точка $x = 5$ является стационарной:

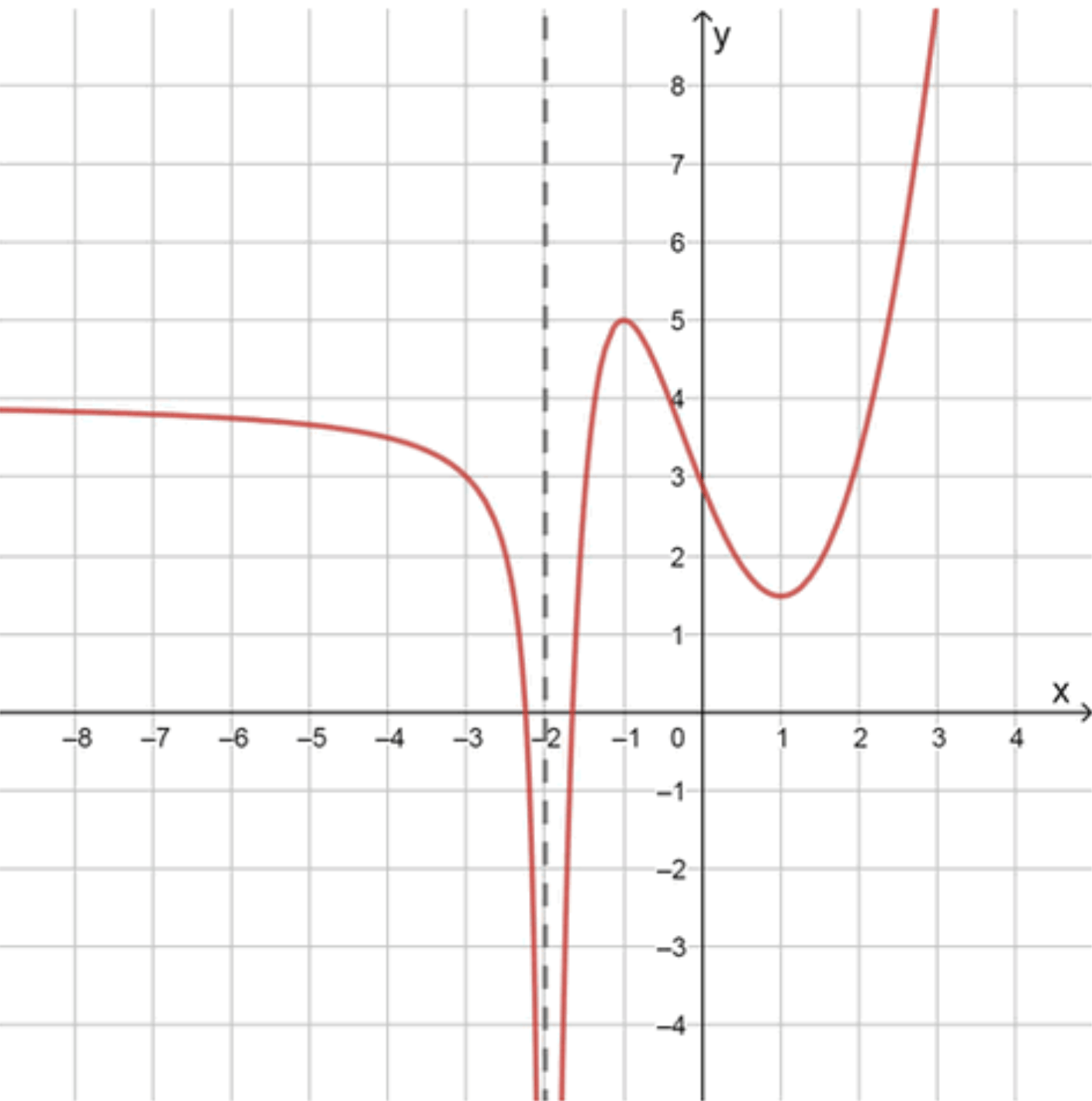
в) Функция имеет разрыв в точке $x = -2$, максимум в точке $x = -1$ и минимум в точке $x = 1$:

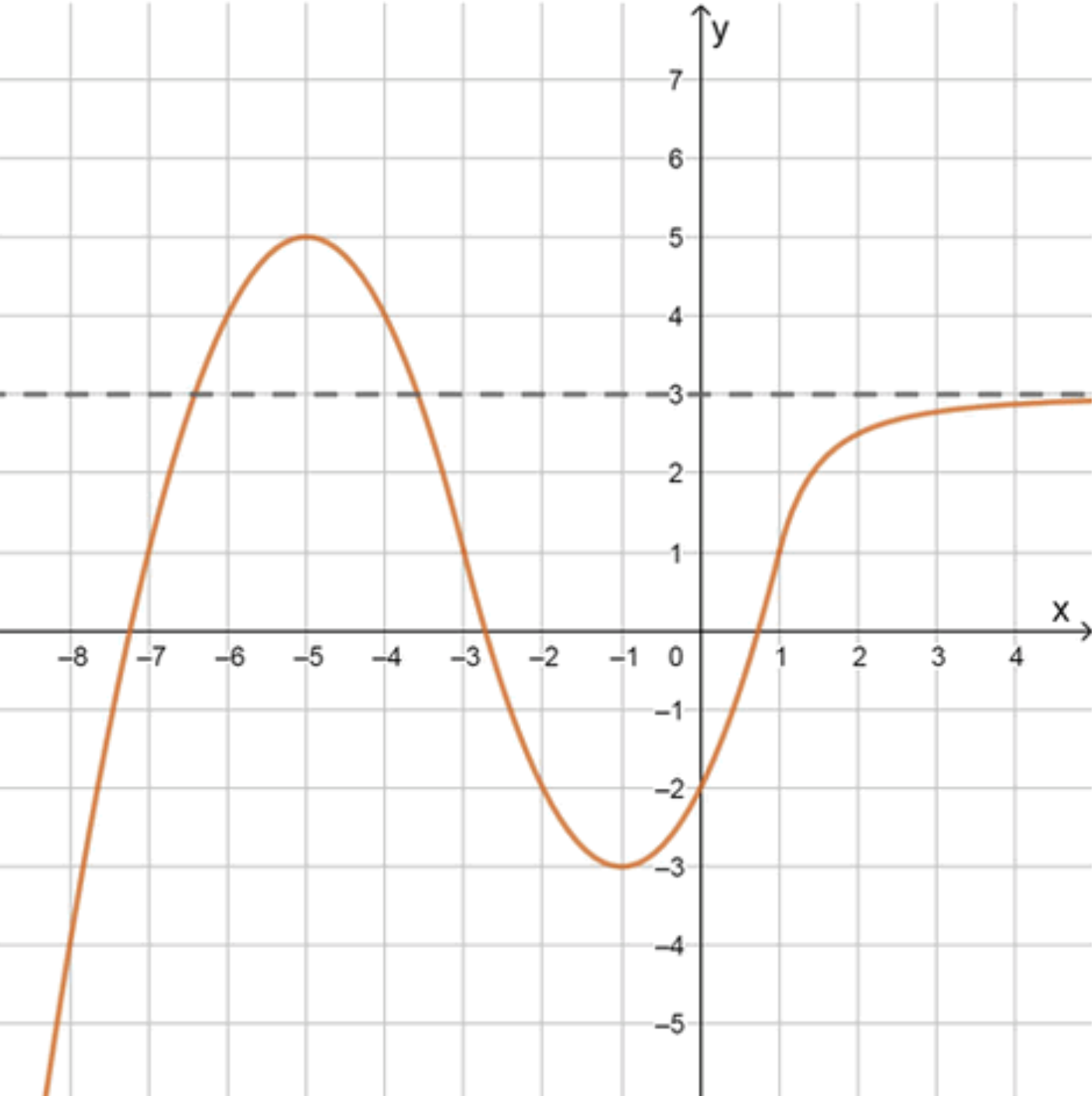
г) Функция имеет горизонтальную асимптоту $y = 3$ при $x \to \infty$, одну точку максимума и одну точку минимума:

Эскиз графика — это приближённое изображение функции, которое отражает:

• характер возрастания и убывания,
• наличие максимумов и минимумов,
• разрывы,
• асимптоты,
• ограниченность и другие качественные свойства.

а) Функция имеет две точки максимума, одну точку минимума и является ограниченной

Что это значит?

• Две точки максимума → две вершины «горок».
• Одна точка минимума → одна впадина между этими горками.
• Ограниченная функция → значения $y$ не выходят за определённые границы (например, не стремятся к $\pm\infty$).

Как построить:

1. Начинаем слева, плавно поднимаемся к первому максимуму.
2. Потом спускаемся к единственному минимуму.
3. Затем снова поднимаемся ко второму максимуму.
4. После — либо спадаем немного, либо выравниваемся (но не уходим в бесконечность!).

Комментарии:

• Вся кривая находится между двумя горизонтальными линиями, например:

  $$-2 \leq y \leq 4$$

• График выглядит как «две горки с впадиной между».

б) Функция возрастает при $x \leq 1$ и $x \geq 5$, убывает на $[1;5]$;

Точка $x = 1$ — критическая, $x = 5$ — стационарная.

Расшифровка:

• Возрастает при $x \leq 1$ — левый участок поднимается.
• Убывает на $[1;5]$ — от вершины вниз.
• Возрастает при $x \geq 5$ — снова идёт вверх.
• Критическая точка $x = 1$ — здесь производная либо равна 0, либо не существует.
• Стационарная точка $x = 5$ — здесь $f'(x) = 0$, то есть горизонтальный касательный.

Как построить:

1. Слева график плавно поднимается до $x = 1$ — вершина, возможно с углом (если производной нет).
2. Затем убывает до $x = 5$ — точка с горизонтальной касательной.
3. После $x = 5$ график снова поднимается — вторая волна.

Комментарии:

• График похож на слегка асимметричную «латинскую букву W».
• Отличие: вершина в $x = 1$ может быть угловой, а в $x = 5$ — гладкая.

в) Функция имеет:

• Разрыв в точке $x = -2$
• Максимум в $x = -1$
• Минимум в $x = 1$

Расшифровка:

• Разрыв — функция не определена или «скачет» в точке $x = -2$.
• Максимум и минимум — стандартные вершины/впадины.

Как построить:

1. До $x = -2$ — произвольное поведение.
2. В точке $x = -2$ — разрыв:
3. Левый и правый пределы могут не совпадать.
4. Можно нарисовать «прыжок» или разрыв первого рода.
5. В точке $x = -1$ — график поднимается до пика.
6. Затем убывает, проходит через $x = 0$, и в точке $x = 1$ — минимум.
7. После $x = 1$ — можно снова поднимать или выравнивать.

Комментарии:

• Функция не непрерывна — в отличие от предыдущих пунктов.
• Можно нарисовать пунктир на месте разрыва и точку в другом месте (прыжок).

г) Функция имеет:

• Горизонтальную асимптоту $y = 3$ при $x \to \infty$
• Один максимум
• Один минимум

Расшифровка:

• При $x \to \infty$, функция приближается к $y = 3$, но не превышает и не уходит выше.
• Должно быть одно «плавное» поднятие и опускание (или наоборот), без других экстремумов.

Как построить:

1. Начинаем с некоторого значения при $x \ll 0$, например, $y = 2$.
2. График возрастает к максимуму.
3. Затем спадает до минимума.
4. Потом медленно возрастает, приближаясь к линии $y = 3$ (не пересекает!).

Комментарии:

• Асимптота — прямая линия, к которой график «прилипает» справа.
• Можно добавить подпись: «асимптота $y = 3$«.
• Только один максимум и один минимум — никаких дополнительных волн!