ГДЗ 10-11 Класс Номер 30.7 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Изобразите эскиз графика производной функции у = f(х), если известно, что функция у = f(х) возрастает на луче ($-\mathrm{\infty }$; 1] и убывает на луче [1; $+\mathrm{\infty }$).

Изобразить эскиз графика производной функции $y = f(x)$, если:

Известно, что функция $y = f(x)$:
– Возрастает на луче $(-\infty; 1]$;
– Убывает на луче $[1; +\infty)$;

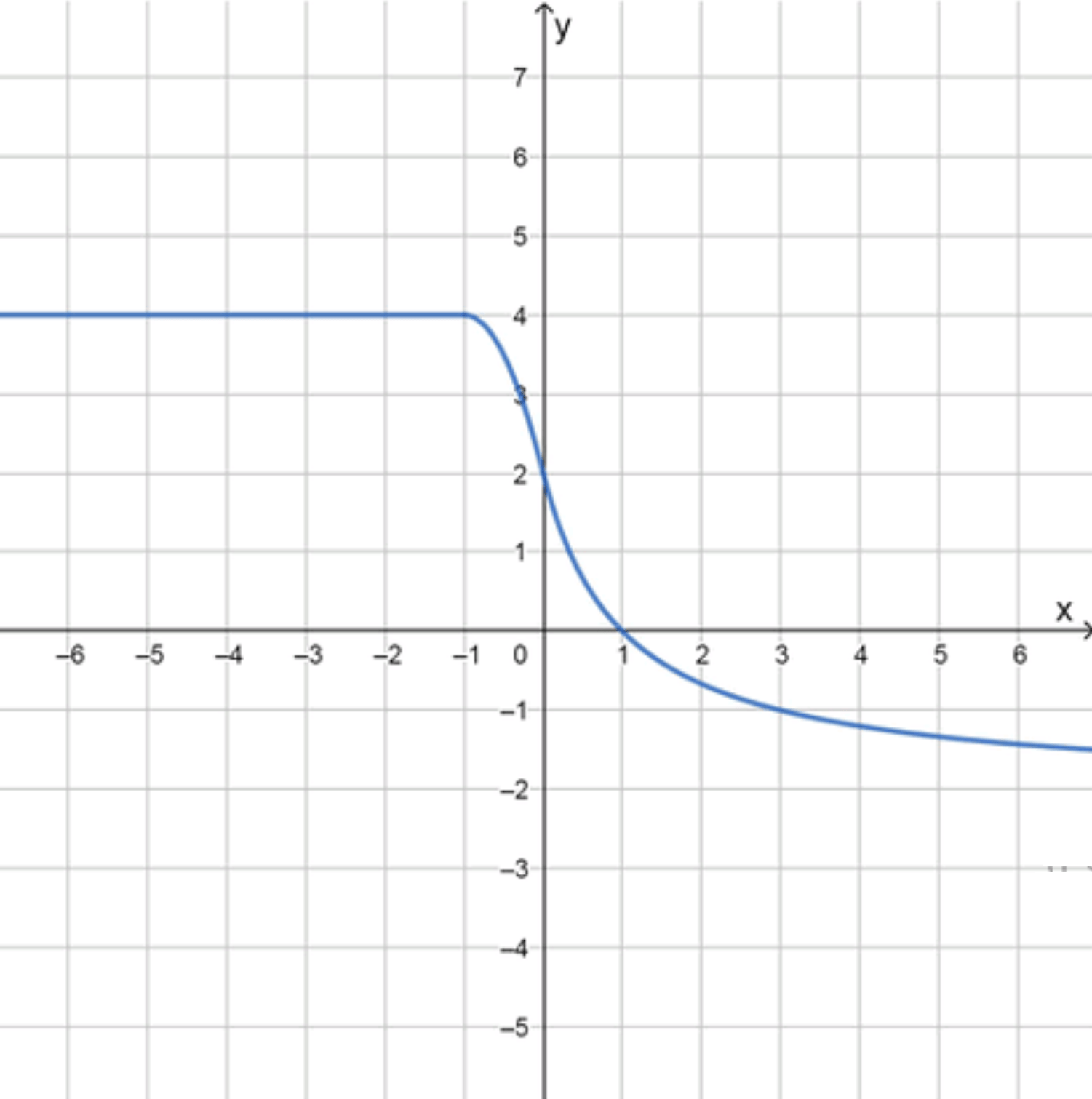
Эскиз графика производной $y = f'(x)$:

Шаг 1. Теория — связь функции и её производной

Напоминаем:

Шаг 2. Расшифруем условие задачи

Дано:

• $f(x)$ возрастает на $(-\infty; 1]$, значит:

  $$f'(x) > 0 \quad \text{для } x < 1$$

• $f(x)$ убывает на $[1; +\infty)$, значит:

  $$f'(x) < 0 \quad \text{для } x > 1$$

• В точке $x = 1$, где смена возрастания на убывание, функция имеет максимум, а значит:

  $$f'(1) = 0$$

Шаг 3. Что это значит для графика производной?

График $y = f'(x)$ будет:

• Выше оси Ox (положительный) на всём интервале $(-\infty; 1)$,
• Пересекает ось Ox в точке $x = 1$ (значение ноль),
• Ниже оси Ox (отрицательный) на интервале $(1; +\infty)$.

Такое поведение характерно для убывающей линейной функции, например:

$$f'(x) = -k(x — 1), \quad k > 0$$

Это просто пример, сама форма может быть любой, главное — знак производной.

Шаг 4. Как выглядит график

Это может быть:

• Гладкая кривая, которая:
  • Находится выше оси Ox слева от 1,
  • Касается оси в точке $x = 1$,
  • Уходит вниз (ниже оси) справа от 1.

В простейшем случае это прямая, наклонённая вниз, пересекающая ось Ox в точке $x = 1$.

Шаг 5. Как построить эскиз графика $y = f'(x)$

Пошаговая инструкция:

• Нарисуйте оси координат $x$ и $y$.
• Отметьте точку $x = 1$ на оси абсцисс.
• В этой точке f'(1) = 0, значит, график пересекает ось Ox здесь.
• Для $x < 1$:
  • Производная $> 0$,
  • График расположен над осью Ox.
• Для $x > 1$:
  • Производная $< 0$,
  • График расположен под осью Ox.
• Соедините плавной кривой:
  • Начинается где-то выше оси Ox при $x \ll 1$,
  • Опускается вниз,
  • Пересекает ось в точке $x = 1$,
  • Продолжает убывать и уходит вниз.

Визуально график напоминает:

• График функции $f'(x) = -x + 1$,
• Или параболу, если производная убывает неравномерно.