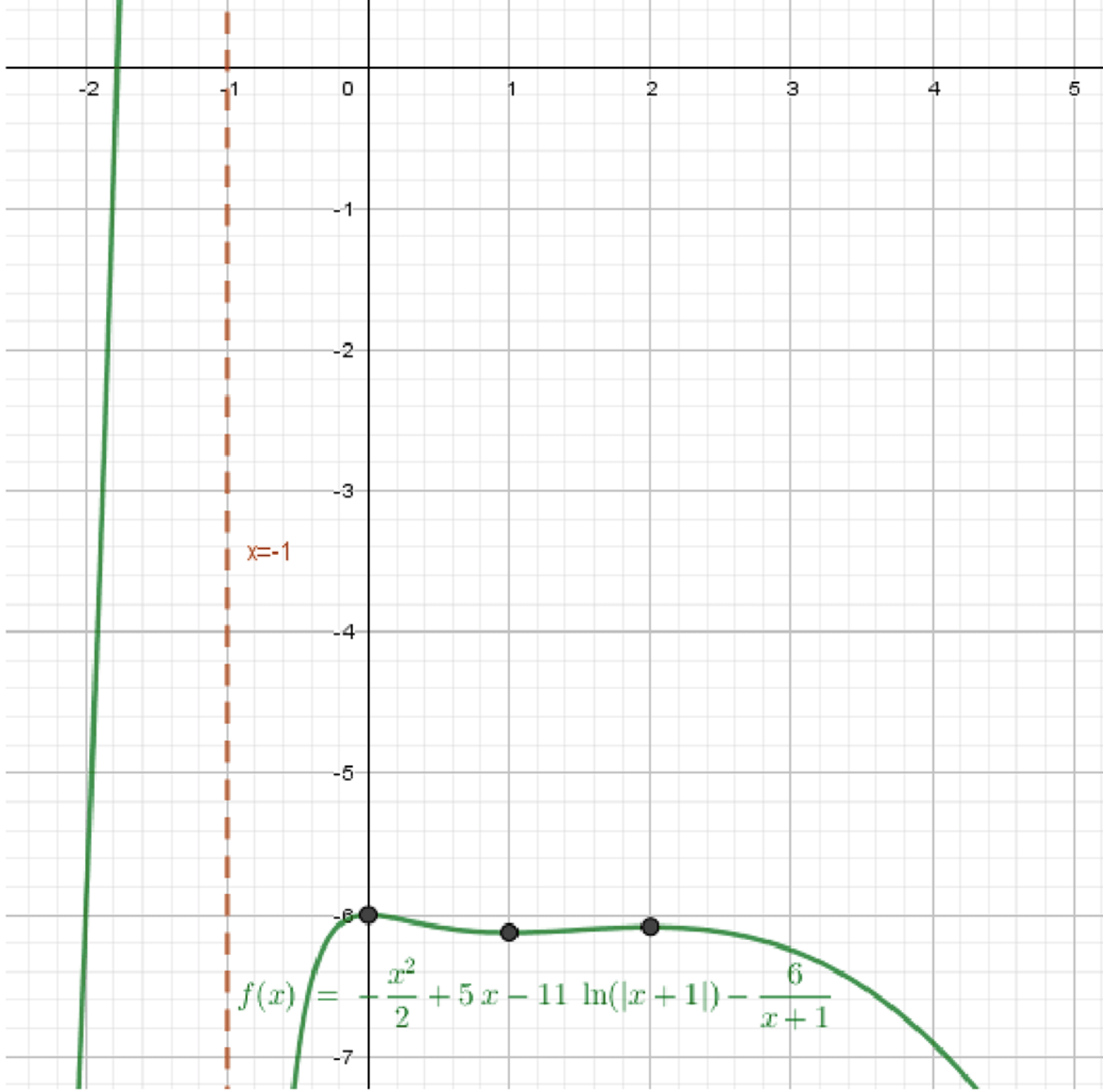ГДЗ 10-11 Класс Номер 30.8 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Изобразите эскиз графика функции у = f(х), если промежутки постоянства знака производной f'(х) представлены на заданной схеме:

а) рис. 60;

б) рис. 61;

в) рис. 62;

г) рис. 63.

Изобразить эскиз графика функции $y = f(x)$, если промежутки постоянства знака производной $f'(x)$ представлены на схеме:

а) Рисунок 60:

б) Рисунок 61:

в) Рисунок 62:

г) Рисунок 63:

БАЗОВАЯ ТЕОРИЯ: как по знаку производной понять поведение функции

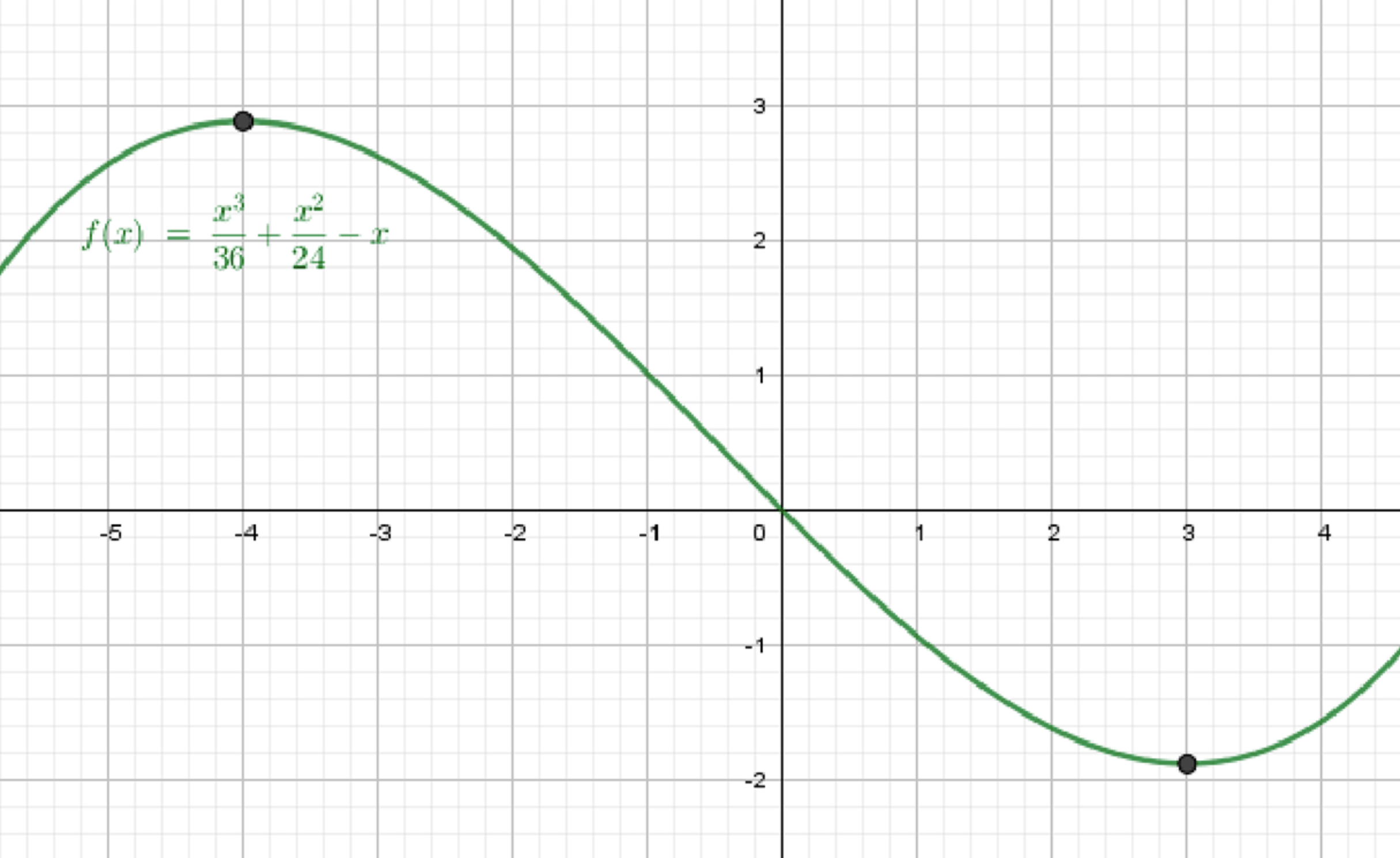
а) Рисунок 60

Интервалы:

• $(-\infty; -4)$: $f'(x) > 0$ ⇒ возрастает
• $(-4; 3)$: $f'(x) < 0$ ⇒ убывает
• $(3; +\infty)$: $f'(x) > 0$ ⇒ возрастает

Что происходит в точках:

• В точке $x = -4$: знак производной меняется с плюса на минус ⇒ максимум
• В точке $x = 3$: знак меняется с минуса на плюс ⇒ минимум

Эскиз графика:

• Функция сначала растёт до точки $x = -4$,
• Затем убывает до точки $x = 3$,
• Потом снова растёт.

Вид: горбик и впадинка
Экстремумы в $x = -4$ (максимум), $x = 3$ (минимум)

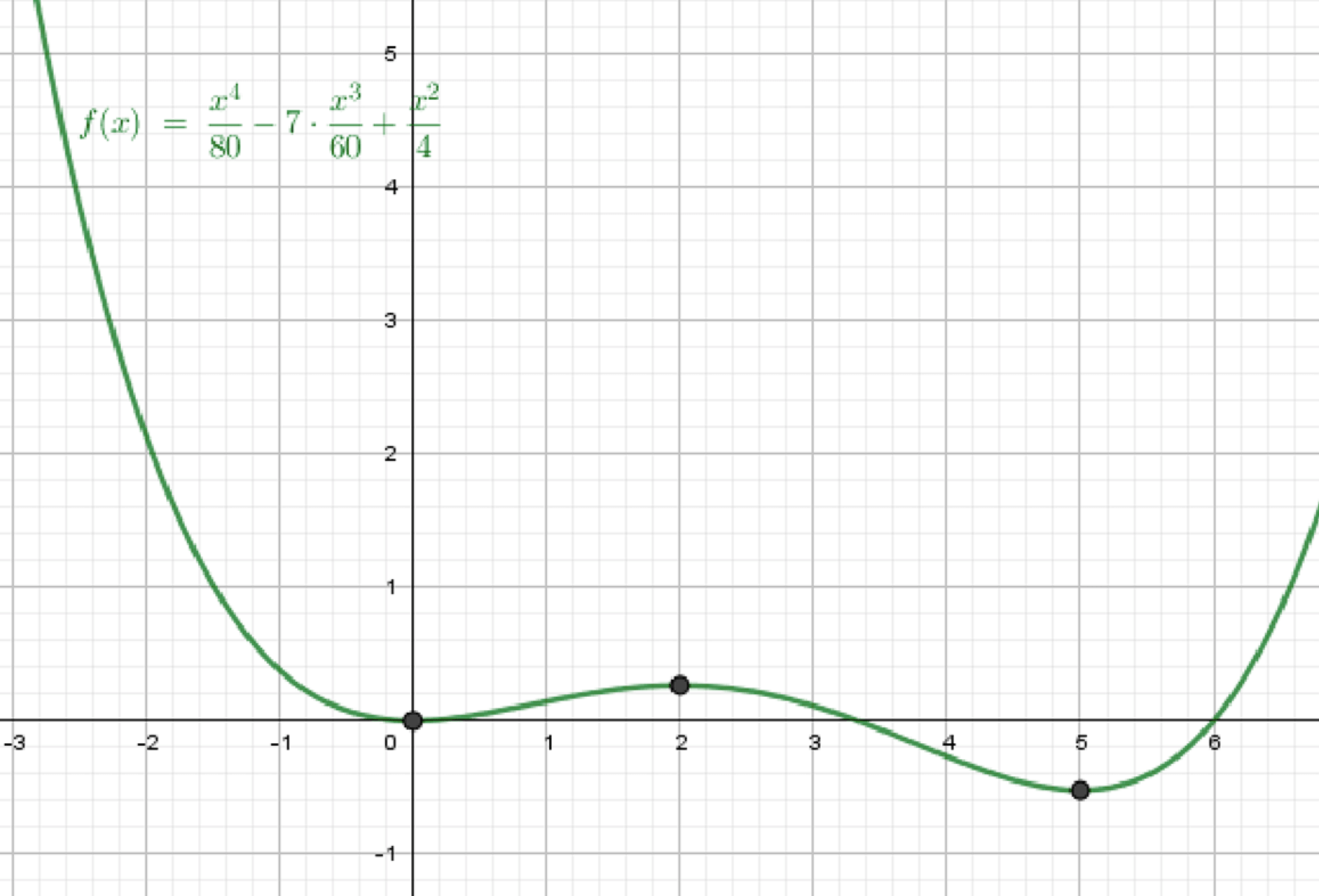
б) Рисунок 61

Интервалы:

• $(-\infty; 0)$: $f'(x) < 0$ ⇒ убывает
• $(0; 2)$: $f'(x) > 0$ ⇒ возрастает
• $(2; 5)$: $f'(x) < 0$ ⇒ убывает
• $(5; +\infty)$: $f'(x) > 0$ ⇒ возрастает

Что происходит в точках:

• $x = 0$: смена минус → плюс ⇒ минимум
• $x = 2$: смена плюс → минус ⇒ максимум
• $x = 5$: смена минус → плюс ⇒ минимум

Эскиз графика:

• Убывает до $x = 0$ → минимум
• Растёт до $x = 2$ → максимум
• Убывает до $x = 5$ → минимум
• Снова растёт

Вид: впадинка – горбик – впадинка – подъём

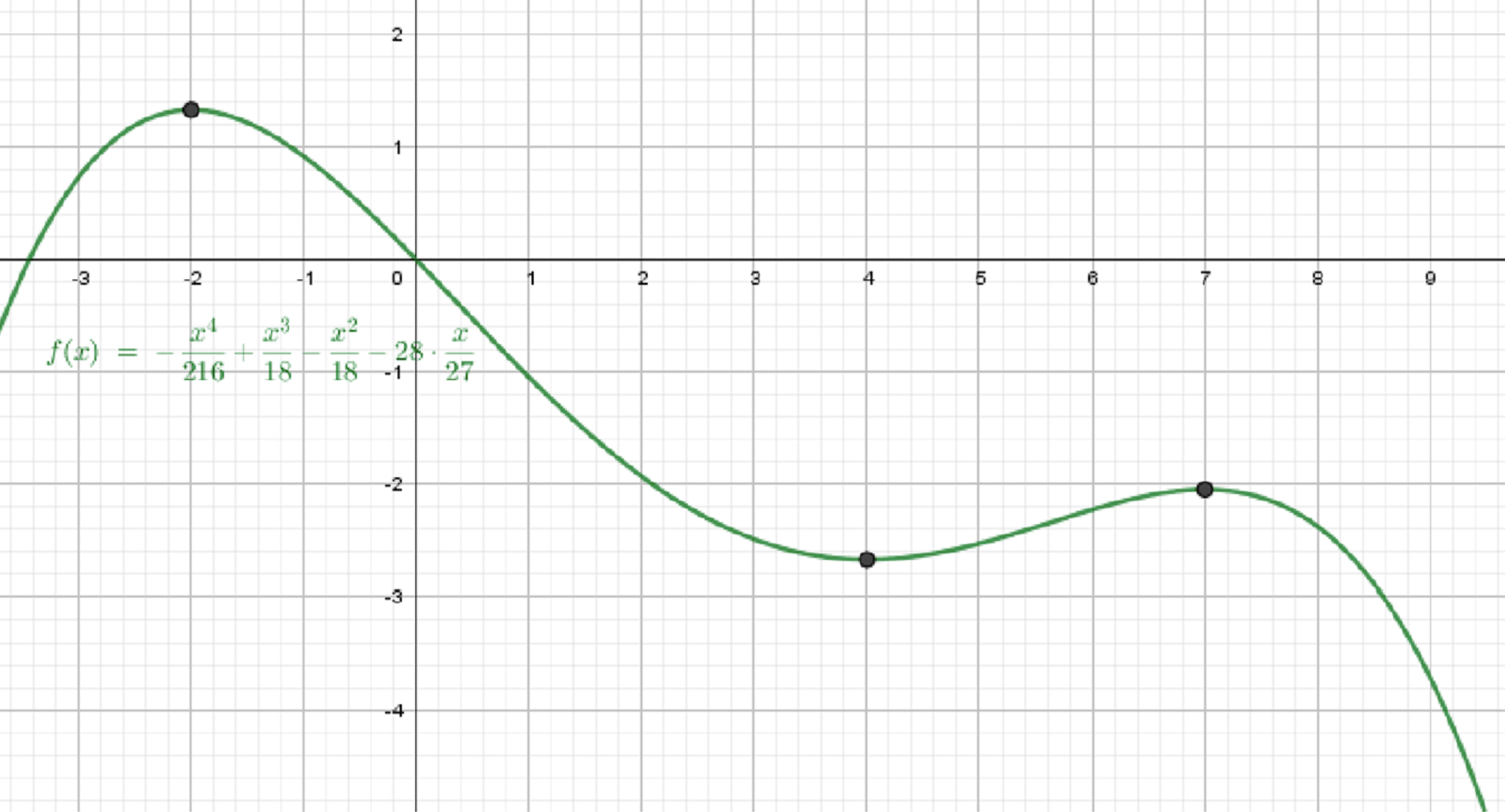
в) Рисунок 62

Интервалы:

• $(-\infty; -2)$: $f'(x) > 0$ ⇒ возрастает
• $(-2; 4)$: $f'(x) < 0$ ⇒ убывает
• $(4; 7)$: $f'(x) > 0$ ⇒ возрастает
• $(7; +\infty)$: $f'(x) < 0$ ⇒ убывает

Что происходит в точках:

• $x = -2$: плюс → минус ⇒ максимум
• $x = 4$: минус → плюс ⇒ минимум
• $x = 7$: плюс → минус ⇒ максимум

Эскиз графика:

• Растёт до $x = -2$ → максимум
• Убывает до $x = 4$ → минимум
• Растёт до $x = 7$ → максимум
• Убывает

Вид: горбик – впадинка – горбик – спад

г) Рисунок 63

Интервалы:

• $(-\infty; -1)$: $f'(x) > 0$ ⇒ возрастает
• $(-1; 0)$: $f'(x) > 0$ ⇒ возрастает
• $(0; 1)$: $f'(x) < 0$ ⇒ убывает
• $(1; 2)$: $f'(x) > 0$ ⇒ возрастает
• $(2; +\infty)$: $f'(x) < 0$ ⇒ убывает

Особенность: производная не меняет знак в точке $x = -1$, оставаясь положительной.

Что происходит в точках:

• $x = 0$: плюс → минус ⇒ максимум
• $x = 1$: минус → плюс ⇒ минимум
• $x = 2$: плюс → минус ⇒ максимум

Эскиз графика:

• Растёт всё до $x = 0$ → максимум
• Убывает до $x = 1$ → минимум
• Растёт до $x = 2$ → максимум
• Убывает

Вид: подъём – максимум – спад – минимум – подъём – максимум – спад