ГДЗ 10-11 Класс Номер 31.1 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте эскиз графика какой-нибудь функции, обладающей указанными свойствами:

а) Функция имеет две точки максимума, одну точку минимума и является ограниченной;

б) функция возрастает при х ≤ 1 и при х ≥ 5 и убывает на промежутке [1; 5]; точка х = 1 является критической, а точка х = 5 — стационарной.

Построить эскиз графика какой-нибудь функции, обладающей указанными свойствами:

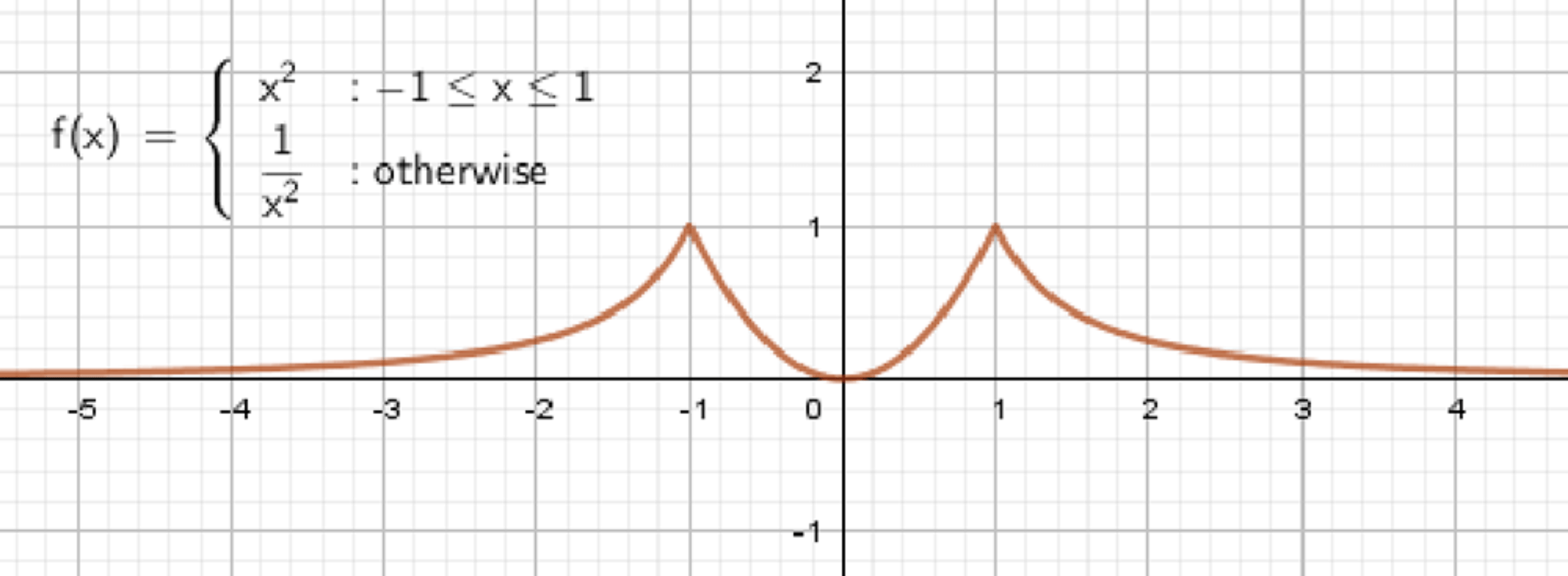
а) Функция имеет две точки максимума, одну точку минимума и является ограниченной:

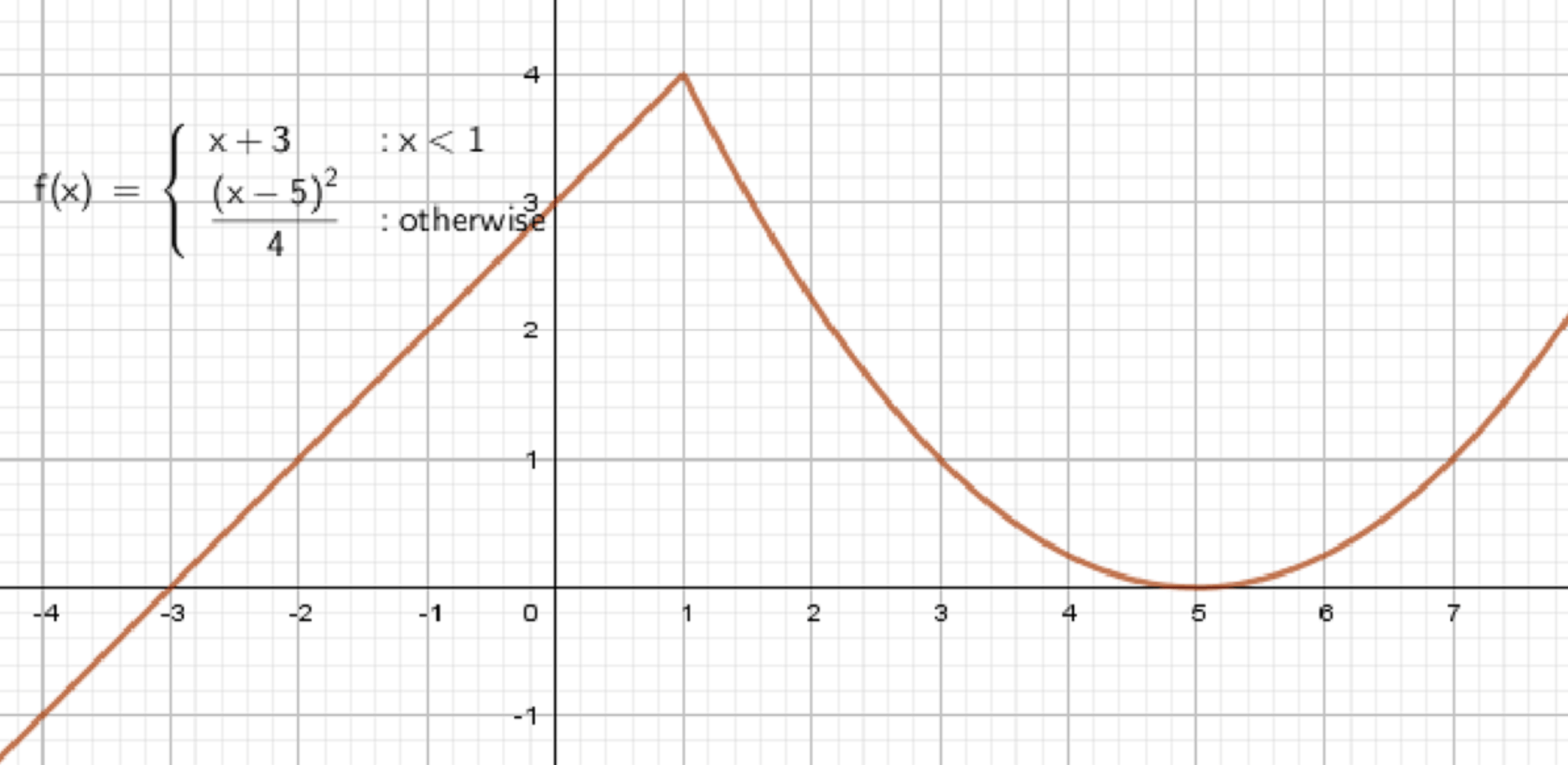
б) Функция возрастает при $x\le 1$ и $x\ge 5$ и убывает на промежутке $[1;5]$; точка $x=1$ является критической, а точка $x=5$ является стационарной:

а) Функция имеет две точки максимума, одну точку минимума и является ограниченной

Шаг 1. Анализ условий

1. Две точки максимума → значит, есть две вершины, в которых функция достигает локального максимального значения.
2. Одна точка минимума → между этими максимумами есть одна вершина вниз.
3. Функция ограничена → значения функции не стремятся к бесконечности, т.е. есть верхняя и нижняя граница.

Вывод:

• График будет волнообразным — сначала подъём к первому максимуму, потом спад к минимуму, затем подъём ко второму максимуму.
• После и до этих точек значения не уходят вверх или вниз бесконечно.
• Пример такого графика: кусок синусоиды или четвертичный многочлен (полином 4-й степени), например:

$$y=-x^4+4x^3-4x^2$$

Этот график:

• имеет две точки максимума
• одну точку минимума
• и уходит в минус на бесконечности, но ты можешь обрезать его в нужной области, чтобы он стал ограниченным.

Как строить:

1. Нарисуй ось координат.
2. Отметь две вершины вверх (точки максимума), пусть они будут в точках $x=-2$ и $x=2$.
3. Между ними, например, в $x=0$, нарисуй точку минимума.
4. За пределами этих точек «обрежь» график (например, по $x=-3$ и $x=3$), чтобы он был ограничен.
5. Убедись, что значения $y$ не выходят за некоторые пределы, например $y\in [-2;3]$.

Визуально:

б) Функция возрастает при $x\le 1$ и $x\ge 5$, убывает на $[1;5]$;

Точка $x=1$ — критическая, $x=5$ — стационарная

Шаг 1. Расшифровка условий

• Возрастает при $x\le 1$ → график поднимается слева до $x=1$.
• Убывает на $[1;5]$ → график идёт вниз от 1 до 5.
• Возрастает при $x\ge 5$ → график снова поднимается после точки 5.
• Точка $x=1$ — критическая → производная равна 0 или не существует.
• Точка $x=5$ — стационарная → производная равна 0.

Вывод:

• $x=1$ — максимум: слева функция росла, справа убывает.
• $x=5$ — минимум: слева убывает, справа возрастает.
• Между ними — «впадина».

Пример функции

Функция, удовлетворяющая таким условиям:

$$y=(x-1{)}^2(x-5)$$

Но нам важно не уравнение, а формирование графика по описанному поведению.

Как строить:

1. Нарисуй ось координат.
2. Построй точку максимума в $x=1$, обозначь её вершиной графика вверх.
3. От этой точки график должен плавно убывать до $x=5$.
4. В точке $x=5$ график достигает минимума, изгибается и идёт вверх.
5. До $x=1$ — график возрастает (поднимается слева вверх к максимуму).
6. После $x=5$ — снова поднимается (рост после минимума).

Визуально: