ГДЗ 10-11 Класс Номер 31.10 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

а) $y={\displaystyle \frac{1}{x^2+1}}$

б) $y=-{\displaystyle \frac{2}{x^2+4}}$

Построить график функции:

а) $y = \dfrac{1}{x^2 + 1}$

1) Область определения функции:
$D(y) = (-\infty; +\infty)$;

2) Функция является четной:
$y(-x) = \dfrac{1}{(-x)^2 + 1} = \dfrac{1}{x^2 + 1} = y(x)$;

3) Уравнения асимптот:

$$y = \lim_{x \to \infty} \dfrac{1}{x^2 + 1} = \lim_{x \to \infty} \dfrac{\frac{1}{x^2}}{1 + \frac{1}{x^2}} = \dfrac{0}{1 + 0} = \dfrac{0}{1} = 0;$$

4) Производная функции:

$$y'(x) = \dfrac{(1)’ \cdot (x^2 + 1) — 1 \cdot (x^2 + 1)’}{(x^2 + 1)^2} = \dfrac{0 \cdot (x^2 + 1) — 1 \cdot (2x + 0)}{(x^2 + 1)^2} = \dfrac{-2x}{(x^2 + 1)^2};$$

Промежуток возрастания:

$$-2x \geq 0 \Rightarrow x \leq 0;$$

$x = 0$ — точка максимума;
$y_{\max} = \dfrac{1}{0^2 + 1} = \dfrac{1}{1} = 1$;

5) Координаты некоторых точек:

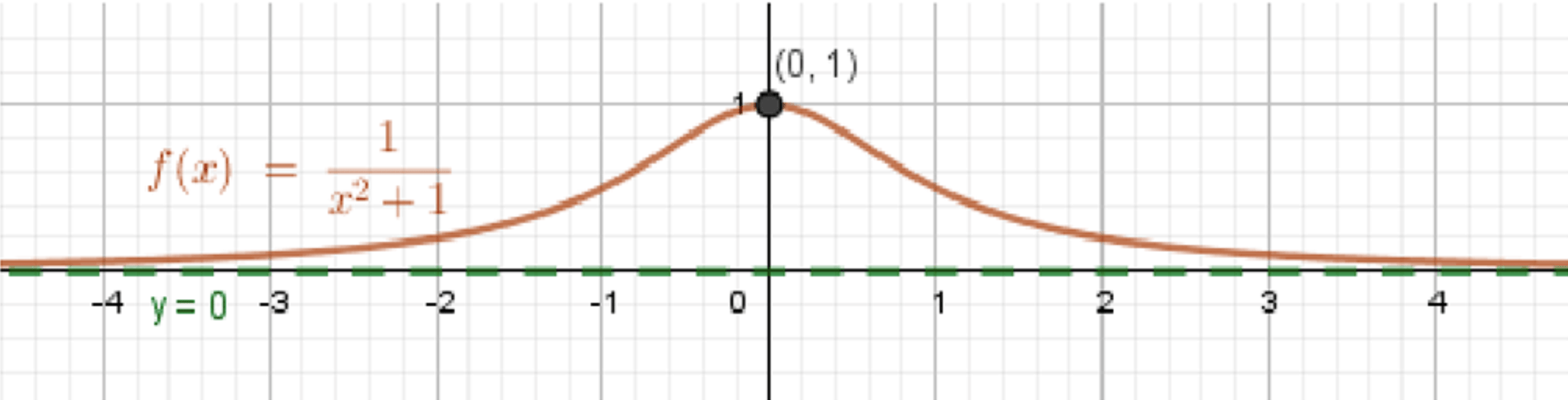
6) График функции:

б) $y = -\dfrac{2}{x^2 + 4}$

1) Область определения функции:
$D(y) = (-\infty; +\infty)$;

2) Функция является четной:
$y(-x) = -\dfrac{2}{(-x)^2 + 4} = -\dfrac{2}{x^2 + 4} = y(x)$;

3) Уравнения асимптот:

$$y = \lim_{x \to \infty} \dfrac{-2}{x^2 + 4} = \lim_{x \to \infty} \dfrac{-\frac{2}{x^2}}{1 + \frac{4}{x^2}} = \dfrac{-0}{1 + 0} = \dfrac{0}{1} = 0;$$

4) Производная функции:

$$y'(x) = -\dfrac{(2)’ \cdot (x^2 + 4) — 2 \cdot (x^2 + 4)’}{(x^2 + 4)^2} = -\dfrac{0 \cdot (x^2 + 4) — 2 \cdot (2x + 0)}{(x^2 + 4)^2} = \dfrac{4x}{(x^2 + 4)^2};$$

Промежуток возрастания:

$$4x \geq 0 \Rightarrow x \geq 0;$$

$x = 0$ — точка минимума;
$y_{\min} = -\dfrac{2}{0^2 + 4} = -\dfrac{2}{4} = -0.5$;

5) Координаты некоторых точек:

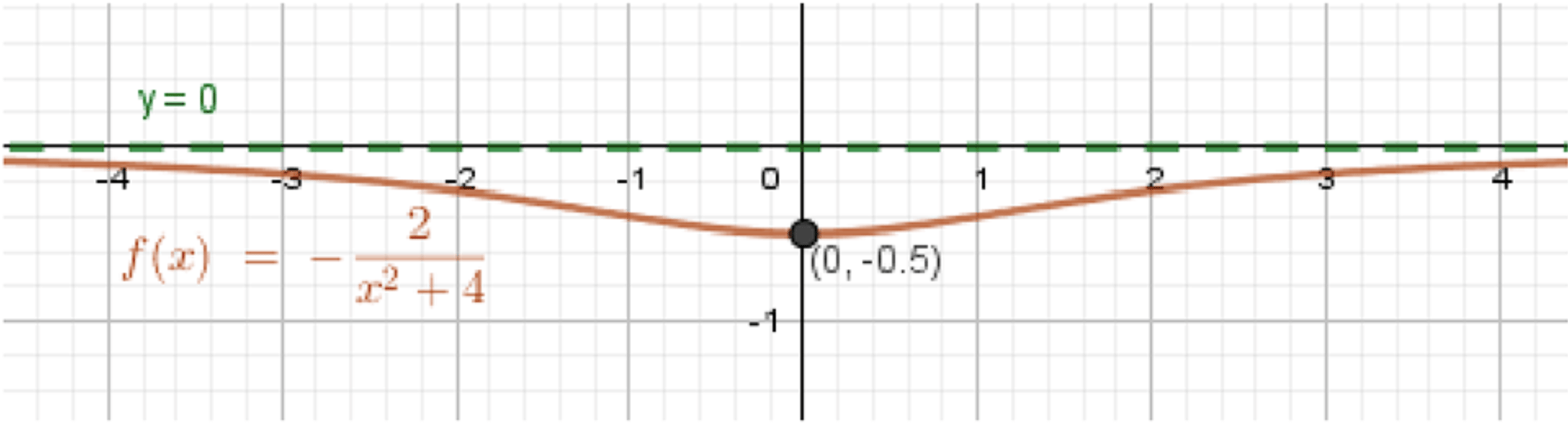
6) График функции:

а) $y = \dfrac{1}{x^2 + 1}$

1. Область определения функции

Функция определена при любом значении $x$, так как в знаменателе стоит выражение $x^2 + 1$, которое всегда положительно:

• $x^2 \geq 0 \Rightarrow x^2 + 1 \geq 1$
• Знаменатель никогда не обращается в ноль

Ответ:

$$D(y) = (-\infty; +\infty)$$

2. Четность функции

Проверим чётность функции:

$$y(-x) = \dfrac{1}{(-x)^2 + 1} = \dfrac{1}{x^2 + 1} = y(x)$$

Следовательно, функция чётная — симметрична относительно оси $OY$.

3. Асимптоты

Вертикальные асимптоты:

• Их нет, потому что знаменатель не обращается в ноль, и $y$ определена при всех $x$

Горизонтальные асимптоты:

Исследуем поведение при $x \to \infty$ и $x \to -\infty$:

$$\lim_{x \to \pm\infty} \dfrac{1}{x^2 + 1} = 0$$

Ответ:
Горизонтальная асимптота — прямая $y = 0$

4. Производная функции

$$y = \dfrac{1}{x^2 + 1} \Rightarrow y’ = \dfrac{0 \cdot (x^2 + 1) — 1 \cdot (2x)}{(x^2 + 1)^2} = \dfrac{-2x}{(x^2 + 1)^2}$$

Исследование производной:

• Знаменатель $(x^2 + 1)^2 > 0$ при любом $x$
• Знак производной зависит только от числителя $-2x$

Следовательно:

• Если $x < 0$, то $y'(x) > 0$ — функция возрастает
• Если $x > 0$, то $y'(x) < 0$ — функция убывает
• При $x = 0$, производная равна нулю: $y'(0) = 0$

Экстремум:

• $x = 0$ — точка максимума (смена знака производной с + на −)

$$y_{\max} = \dfrac{1}{0^2 + 1} = 1$$

5. Таблица значений

Вычислим значения функции в нескольких точках:

6. Поведение графика

• График симметричен относительно оси $OY$
• Имеет максимум в точке $(0; 1)$
• Убывает при $x > 0$, возрастает при $x < 0$
• При $x \to \pm\infty$, $y \to 0$ (асимптота $y = 0$)
• Значения функции всегда положительные: $y > 0$

б) $y = -\dfrac{2}{x^2 + 4}$

1. Область определения функции

Знаменатель: $x^2 + 4 > 0$ при всех $x$, т.к. $x^2 \geq 0$, значит $x^2 + 4 \geq 4$

Ответ:

$$D(y) = (-\infty; +\infty)$$

2. Четность функции

$$y(-x) = -\dfrac{2}{(-x)^2 + 4} = -\dfrac{2}{x^2 + 4} = y(x)$$

Функция — чётная, симметрична относительно оси $OY$

3. Асимптоты

Вертикальных асимптот нет:

• Знаменатель не обращается в 0

Горизонтальная асимптота:

$$\lim_{x \to \pm\infty} \dfrac{-2}{x^2 + 4} = 0$$

Ответ:
$y = 0$ — горизонтальная асимптота

4. Производная функции

$$y = -\dfrac{2}{x^2 + 4} \Rightarrow y'(x) = -\dfrac{0 \cdot (x^2 + 4) — 2 \cdot 2x}{(x^2 + 4)^2} = \dfrac{4x}{(x^2 + 4)^2}$$

Исследование производной:

• Знаменатель положительный
• Знак производной определяется по $4x$

Следовательно:

• $x < 0 \Rightarrow y'(x) < 0$: функция убывает
• $x > 0 \Rightarrow y'(x) > 0$: функция возрастает
• $x = 0 \Rightarrow y'(x) = 0$: стационарная точка

Экстремум:

• $x = 0$ — минимум, так как производная меняет знак с минуса на плюс

$$y_{\min} = -\dfrac{2}{0^2 + 4} = -\dfrac{2}{4} = -0.5$$

5. Таблица значений

6. Поведение графика

• Чётная функция: симметрия относительно оси $OY$
• Минимум в точке $(0; -0.5)$
• Убывает при $x < 0$, возрастает при $x > 0$
• Значения функции всегда отрицательные
• При $x \to \pm\infty$, $y\to 0^{-}$