ГДЗ 10-11 Класс Номер 31.11 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y={\displaystyle \frac{2x+1}{x^2+2}}$;

б) $y={\displaystyle \frac{x-2}{x^2+5}}$

Построить график функции:

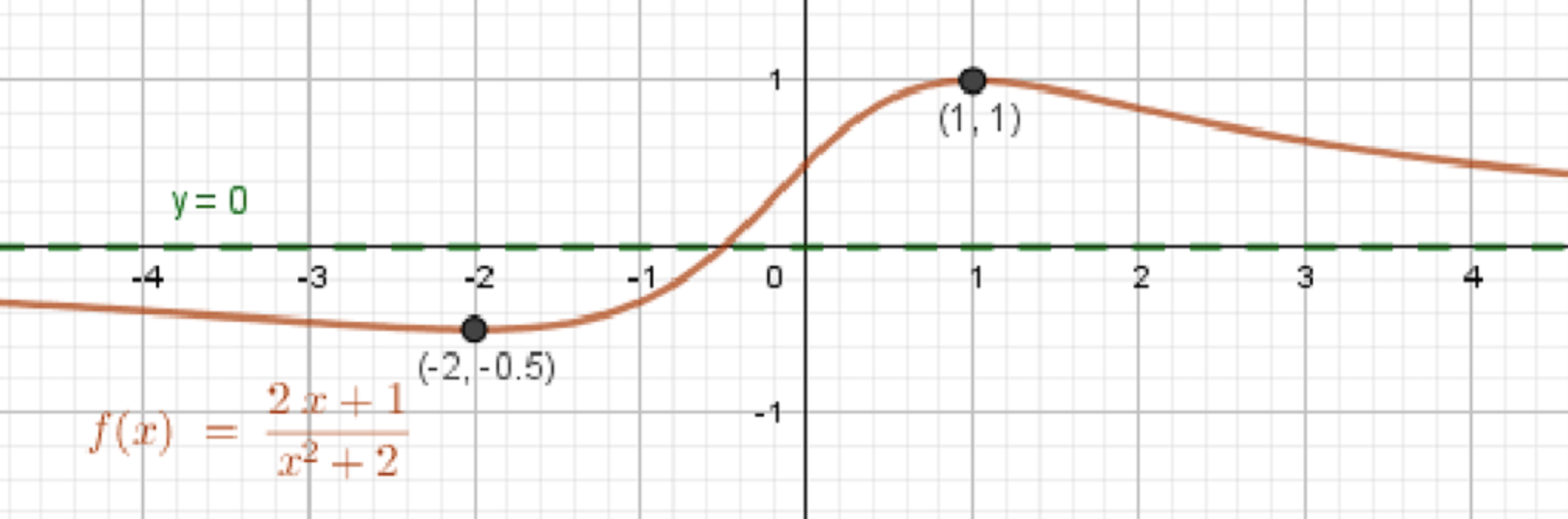
а) $y={\displaystyle \frac{2x+1}{x^2+2}}$;

Область определения функции:
$D(y)=(-\mathrm{\infty };+\mathrm{\infty })$;

Уравнения асимптот:
$y={\lim }_{x\to \mathrm{\infty }}{\displaystyle \frac{2x+1}{x^2+2}}={\lim }_{x\to \mathrm{\infty }}{\displaystyle \frac{{\displaystyle \frac{2}{x}}+{\displaystyle \frac{1}{x^2}}}{1+{\displaystyle \frac{2}{x^2}}}}={\displaystyle \frac{0+0}{1+0}}={\displaystyle \frac{0}{1}}=0$;

Производная функции:
$y^{\mathrm{\prime }}(x)={\displaystyle \frac{(2x+1{)}^{\mathrm{\prime }}\cdot (x^2+2)-(2x+1)\cdot (x^2+2{)}^{\mathrm{\prime }}}{(x^2+2{)}^2}}$;
$y^{\mathrm{\prime }}(x)={\displaystyle \frac{2\cdot (x^2+2)-(2x+1)\cdot 2x}{(x^2+2{)}^2}}$;
$y^{\mathrm{\prime }}(x)={\displaystyle \frac{2x^2+4-4x^2-2x}{(x^2+2{)}^2}}={\displaystyle \frac{4-2x-2x^2}{(x^2+2{)}^2}}$;

Промежуток возрастания:
$4-2x-2x^2\ge 0\mathrm{\mid }:(-2)$;
$x^2+x-2\le 0$;
$D=1^2+4\cdot 2=1+8=9$, тогда:
$x_1={\displaystyle \frac{-1-3}{2}}=-2$ и $x_2={\displaystyle \frac{-1+3}{2}}=1$;
$(x+2)(x-1)\le 0$;
$-2\le x\le 1$;
$x=-2$ — точка минимума;
$x=1$ — точка максимума;
$y_{\min }={\displaystyle \frac{2\cdot (-2)+1}{(-2{)}^2+2}}={\displaystyle \frac{-4+1}{4+2}}={\displaystyle \frac{-3}{6}}=-{\displaystyle \frac{1}{2}}$;
$y_{\max }={\displaystyle \frac{2\cdot 1+1}{1^2+2}}={\displaystyle \frac{2+1}{1+2}}={\displaystyle \frac{3}{3}}=1$;

Координаты некоторых точек:

График функции:

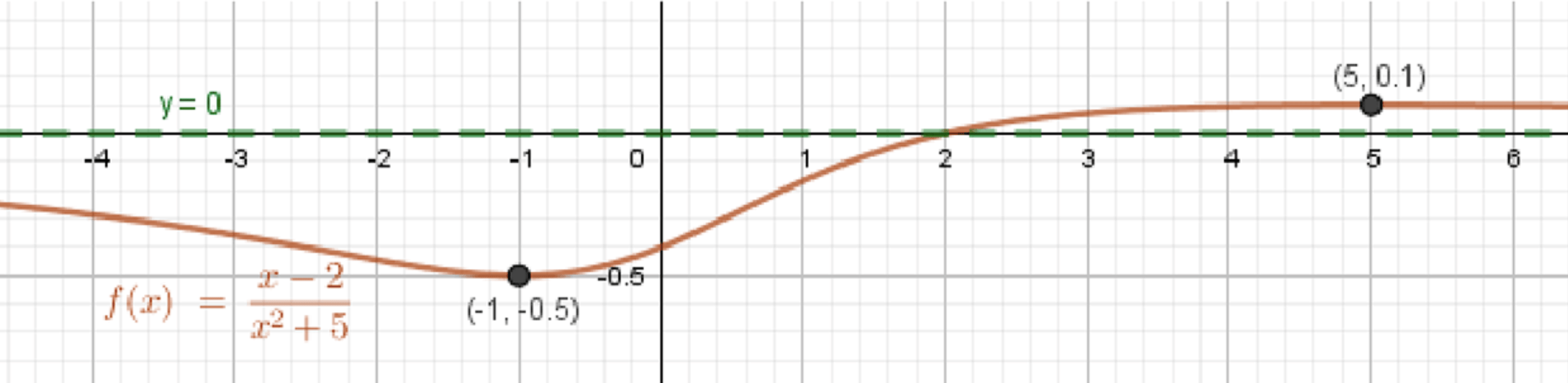
б) $y={\displaystyle \frac{x-2}{x^2+5}}$;

Область определения функции:
$D(y)=(-\mathrm{\infty };+\mathrm{\infty })$;

Уравнения асимптот:
$y={\lim }_{x\to \mathrm{\infty }}{\displaystyle \frac{x-2}{x^2+5}}={\lim }_{x\to \mathrm{\infty }}{\displaystyle \frac{{\displaystyle \frac{1}{x}}-{\displaystyle \frac{2}{x^2}}}{1+{\displaystyle \frac{5}{x^2}}}}={\displaystyle \frac{0-0}{1+0}}={\displaystyle \frac{0}{1}}=0$;

Производная функции:
$y^{\mathrm{\prime }}(x)={\displaystyle \frac{(x-2{)}^{\mathrm{\prime }}\cdot (x^2+5)-(x-2)\cdot (x^2+5{)}^{\mathrm{\prime }}}{(x^2+5{)}^2}}$;
$y^{\mathrm{\prime }}(x)={\displaystyle \frac{1\cdot (x^2+5)-(x-2)\cdot 2x}{(x^2+5{)}^2}}$;
$y^{\mathrm{\prime }}(x)={\displaystyle \frac{x^2+5-2x^2+4x}{(x^2+5{)}^2}}={\displaystyle \frac{5+4x-x^2}{(x^2+5{)}^2}}$;

Промежуток возрастания:
$5+4x-x^2\ge 0\mathrm{\mid }:(-1)$;
$x^2-4x-5\le 0$;
$D=4^2+4\cdot 5=16+20=36$, тогда:
$x_1={\displaystyle \frac{4-6}{2}}=-1$ и $x_2={\displaystyle \frac{4+6}{2}}=5$;
$(x+1)(x-5)\le 0$;
$-1\le x\le 5$;
$x=-1$ — точка минимума;
$x=5$ — точка максимума;
$y_{\min }={\displaystyle \frac{-1-2}{(-1{)}^2+5}}={\displaystyle \frac{-3}{1+5}}={\displaystyle \frac{-3}{6}}=-{\displaystyle \frac{1}{2}}$;
$y_{\max }={\displaystyle \frac{5-2}{5^2+5}}={\displaystyle \frac{3}{25+5}}={\displaystyle \frac{3}{30}}={\displaystyle \frac{1}{10}}$;

Координаты некоторых точек:

График функции:

а) $y={\displaystyle \frac{2x+1}{x^2+2}}$

1) Область определения функции

Функция — дробь: числитель $2x+1$, знаменатель $x^2+2$.

Чтобы определить область определения функции, нужно найти, при каких значениях $x$ функция не определена, т.е. когда знаменатель обращается в ноль:

$$x^2+2=0\Rightarrow x^2=-2\Rightarrow \text{Нет решений в вещественных числах}$$

Значит, знаменатель не обращается в ноль нигде, и функция определена при всех значениях $x$.

Ответ:

$$D(y)=(-\mathrm{\infty };+\mathrm{\infty })$$

2) Асимптоты функции

Горизонтальная асимптота (так как знаменатель квадратичный, а числитель линейный)

Исследуем поведение функции при $x\to \mathrm{\infty }$ и $x\to -\mathrm{\infty }$:

$$\underset{x\to \pm \mathrm{\infty }}{\lim }\frac{2x+1}{x^2+2}$$

Доминирующие члены:

• числитель: $2x$
• знаменатель: $x^2$

Чтобы упростить предел, разделим числитель и знаменатель на $x^2$:

$$\underset{x\to \mathrm{\infty }}{\lim }\frac{2x+1}{x^2+2}=\underset{x\to \mathrm{\infty }}{\lim }\frac{\frac{2}{x}+\frac{1}{x^2}}{1+\frac{2}{x^2}}=\frac{0+0}{1+0}=0$$

Аналогично и при $x\to -\mathrm{\infty }$: тоже $y\to 0$

Вывод:
Функция имеет горизонтальную асимптоту $y=0$ (ось абсцисс).

Вертикальной асимптоты нет, так как знаменатель не обращается в ноль ни при каких $x$.

3) Производная функции. Исследование на возрастание/убывание

Функция:

$$y(x)=\frac{2x+1}{x^2+2}$$

Используем правило дифференцирования частного:

$$y^{\mathrm{\prime }}(x)=\frac{u^{\mathrm{\prime }}v-u{v}^{\mathrm{\prime }}}{v^2},\text{где }u=2x+1,v=x^2+2$$

Находим производные:

• $u^{\mathrm{\prime }}=(2x+1{)}^{\mathrm{\prime }}=2$
• $v^{\mathrm{\prime }}=(x^2+2{)}^{\mathrm{\prime }}=2x$

Подставляем:

$$y^{\mathrm{\prime }}(x)=\frac{2(x^2+2)-(2x+1)(2x)}{(x^2+2{)}^2}$$

Раскрываем скобки:

• $2(x^2+2)=2x^2+4$
• $(2x+1)(2x)=4x^2+2x$

Теперь:

$$y^{\mathrm{\prime }}(x)=\frac{2x^2+4-4x^2-2x}{(x^2+2{)}^2}=\frac{-2x^2-2x+4}{(x^2+2{)}^2}=\frac{4-2x-2x^2}{(x^2+2{)}^2}$$

Промежутки возрастания и убывания

Знаменатель $(x^2+2{)}^2>0$ всегда, потому что $x^2+2>0$

Чтобы узнать знаки производной, исследуем числитель:

$$4-2x-2x^2\ge 0\Rightarrow -2x^2-2x+4\ge 0\Rightarrow x^2+x-2\le 0$$

$$(\text{домножили на }-1,\text{знакнеравенстваизменили})$$

Решим квадратное неравенство:

$$x^2+x-2=0\Rightarrow D=1^2+4\cdot 2=9\Rightarrow x_1=\frac{-1-3}{2}=-2,x_2=\frac{-1+3}{2}=1$$

Решение неравенства:

$$(x+2)(x-1)\le 0\Rightarrow x\in [-2;1]$$

Вывод:

• На промежутке $[-2;1]$ функция возрастает
• На промежутках $(-\mathrm{\infty };-2)\cup (1;+\mathrm{\infty })$ функция убывает

Точки экстремума (максимума и минимума)

Производная обращается в ноль при:

$$4-2x-2x^2=0\Rightarrow x^2+x-2=0\Rightarrow x=-2,1$$

• $x=-2$: левее производная положительная, правее — отрицательная ⇒ минимум
• $x=1$: левее производная положительная, правее — отрицательная ⇒ максимум

Найдём значения функции:

• $y_{\min }={\displaystyle \frac{2(-2)+1}{(-2{)}^2+2}}={\displaystyle \frac{-4+1}{4+2}}={\displaystyle \frac{-3}{6}}=-{\displaystyle \frac{1}{2}}$
• $y_{\max }={\displaystyle \frac{2(1)+1}{1^2+2}}={\displaystyle \frac{3}{3}}=1$

4) Таблица значений (некоторые точки)

5) Словесное описание графика

• График гладкий (без разрывов)
• Определён при всех $x\in \mathbb{R}$
• Имеет горизонтальную асимптоту $y=0$
• Максимум при $x=1$, $y=1$
• Минимум при $x=-2$, $y=-{\displaystyle \frac{1}{2}}$
• Симметрии нет (функция ни чётная, ни нечётная)
• Кривая спадает при $x<-2$ и $x>1$, возрастает на $[-2;1]$

б) $y={\displaystyle \frac{x-2}{x^2+5}}$

1) Область определения функции

Знаменатель: $x^2+5>0$ при любом $x\in \mathbb{R}$
(так как $x^2\ge 0$, а $x^2+5\ge 5$)

Ответ:

$$D(y)=(-\mathrm{\infty };+\mathrm{\infty })$$

2) Асимптоты функции

Горизонтальная асимптота:

$$\underset{x\to \mathrm{\infty }}{\lim }\frac{x-2}{x^2+5}\Rightarrow \text{делим числитель и знаменатель на }{x}^2:\Rightarrow \frac{\frac{1}{x}-\frac{2}{x^2}}{1+\frac{5}{x^2}}\to \frac{0-0}{1+0}=0$$

Аналогично при $x\to -\mathrm{\infty }$: $y\to 0$

Ответ: горизонтальная асимптота: $y=0$

Вертикальной асимптоты нет, т.к. знаменатель не обращается в ноль

3) Производная функции

$$y(x)=\frac{x-2}{x^2+5}\Rightarrow u=x-2,v=x^2+5\Rightarrow u^{\mathrm{\prime }}=1,v^{\mathrm{\prime }}=2x$$$$y^{\mathrm{\prime }}(x)=\frac{(x^2+5)\cdot 1-(x-2)(2x)}{(x^2+5{)}^2}$$

Раскрываем:

• $(x-2)(2x)=2x^2-4x$

Теперь:

$$y^{\mathrm{\prime }}(x)=\frac{x^2+5-(2x^2-4x)}{(x^2+5{)}^2}=\frac{x^2+5-2x^2+4x}{(x^2+5{)}^2}=\frac{-x^2+4x+5}{(x^2+5{)}^2}$$

Исследуем знак производной

Числитель: $-x^2+4x+5\ge 0$

Домножим на $-1$, поменяем знак:

$$x^2-4x-5\le 0$$

Решим квадратное неравенство:

$$D=16+20=36,x_1=\frac{4-6}{2}=-1,$$

$$x_2=\frac{4+6}{2}=5\Rightarrow (x+1)(x-5)\le 0\Rightarrow x\in [-1;5]$$

Точки экстремума

Производная равна нулю при $x=-1$ и $x=5$

• $x=-1$: левее производная положительна, правее — отрицательна ⇒ минимум
• $x=5$: левее производная положительна, правее — отрицательна ⇒ максимум

Значения функции:

• $y_{\min }={\displaystyle \frac{-1-2}{(-1{)}^2+5}}={\displaystyle \frac{-3}{6}}=-{\displaystyle \frac{1}{2}}$
• $y_{\max }={\displaystyle \frac{5-2}{25+5}}={\displaystyle \frac{3}{30}}={\displaystyle \frac{1}{10}}$

4) Таблица значений (некоторые точки)

5) Словесное описание графика

• График функции непрерывен на всей числовой прямой
• Имеет горизонтальную асимптоту $y=0$
• Возрастает на $[-1;5]$, убывает вне этого промежутка
• Минимум при $x=-1$, значение $-{\displaystyle \frac{1}{2}}$
• Максимум при $x=5$, значение ${\displaystyle \frac{1}{10}}$
• Кривая проходит через точки $(0;-\mathrm{0,4})$, $(2;0)$