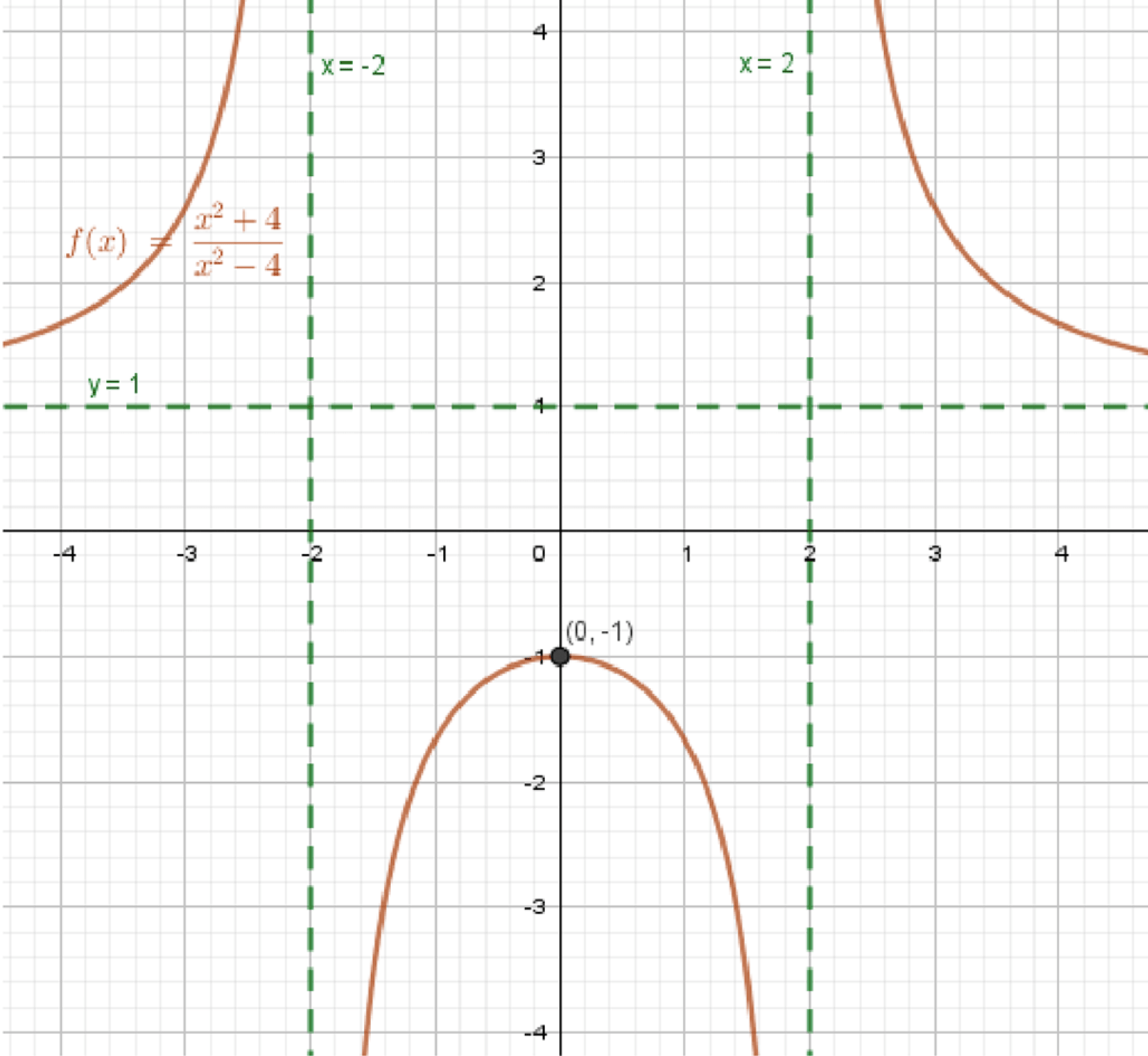ГДЗ 10-11 Класс Номер 31.12 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Построить график функции:

a) $y = \frac{x^2 + 4}{x^2 — 4}$;

Область определения функции:
$x^2 — 4 \neq 0$;
$x^2 \neq 4$;
$x \neq \pm 2$;
$D(y) = (-\infty; -2) \cup (-2; 2) \cup (2; +\infty)$;

Функция является четной:
$y(-x) = \frac{(-x)^2 + 4}{(-x)^2 — 4} = \frac{x^2 + 4}{x^2 — 4} = y(x)$;

Уравнения асимптот:
$x = -2, \; x = 2$;
$y = \lim_{x \to \infty} \frac{x^2 + 4}{x^2 — 4} = \lim_{x \to \infty} \frac{1 + \frac{4}{x^2}}{1 — \frac{4}{x^2}} = \frac{1 + 0}{1 — 0} = \frac{1}{1} = 1$;

Производная функции:
$y'(x) = \frac{(x^2 + 4)’ \cdot (x^2 — 4) — (x^2 + 4) \cdot (x^2 — 4)’}{(x^2 — 4)^2}$;
$y'(x) = \frac{2x \cdot (x^2 — 4) — (x^2 + 4) \cdot 2x}{(x^2 — 4)^2}$;
$y'(x) = \frac{2x^3 — 8x — 2x^3 — 8x}{(x^2 — 4)^2} = \frac{-16x}{(x^2 — 4)^2}$;

Промежуток возрастания:
$-16x \geq 0$;
$x \leq 0$;
$x = 0$ — точка максимума;
$y_{\max} = \frac{0^2 + 4}{0^2 — 4} = \frac{4}{-4} = -1$;

График функции:

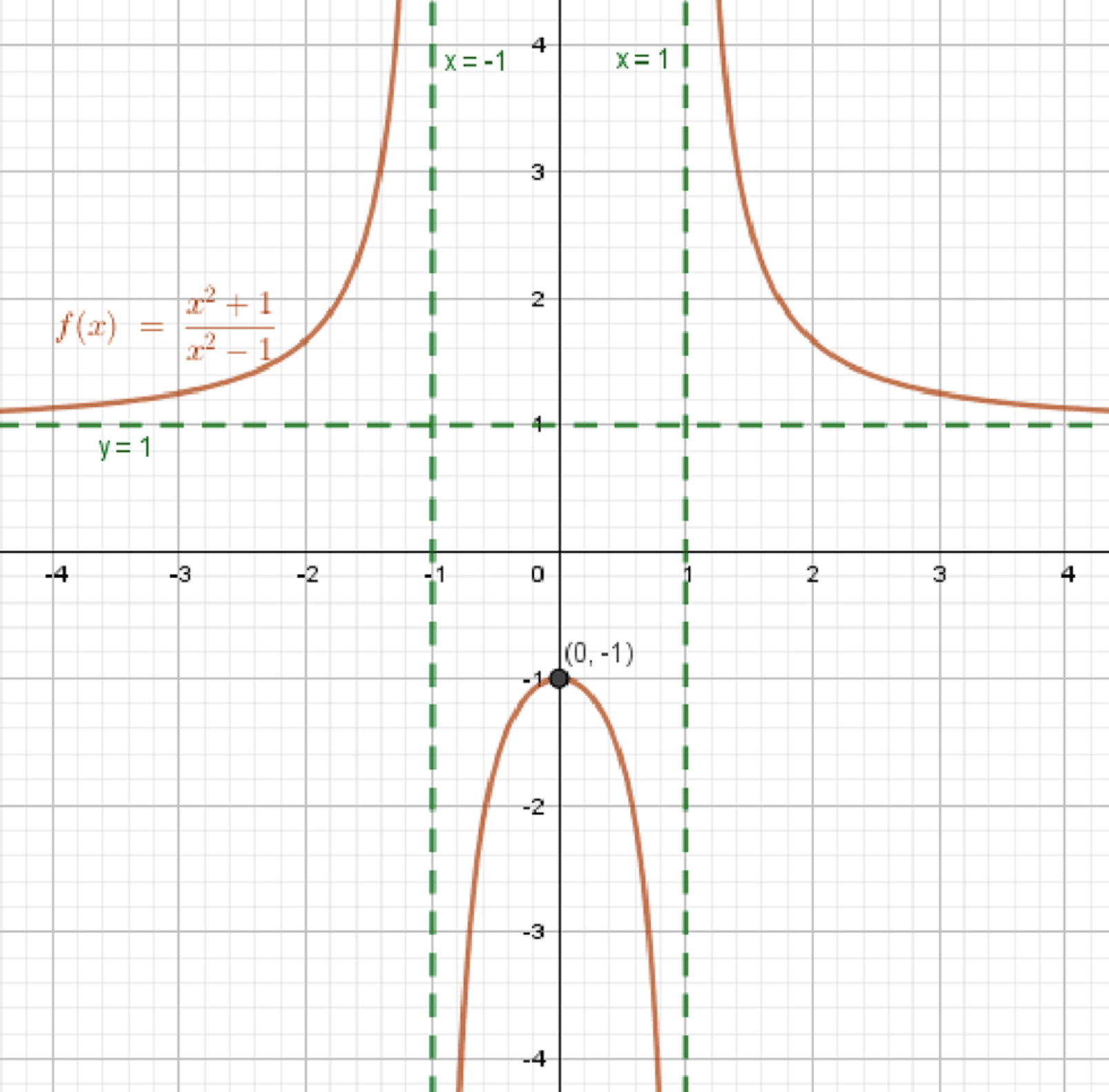
б) $y = \frac{x^2 + 1}{x^2 — 1}$;

Область определения функции:
$x^2 — 1 \neq 0$;
$x^2 \neq 1$;
$x \neq \pm 1$;
$D(y) = (-\infty; -1) \cup (-1; 1) \cup (1; +\infty)$;

Функция является четной:
$y(-x) = \frac{(-x)^2 + 1}{(-x)^2 — 1} = \frac{x^2 + 1}{x^2 — 1} = y(x)$;

Уравнения асимптот:
$x = -1, \; x = 1$;
$y = \lim_{x \to \infty} \frac{x^2 + 1}{x^2 — 1} = \lim_{x \to \infty} \frac{1 + \frac{1}{x^2}}{1 — \frac{1}{x^2}} = \frac{1 + 0}{1 — 0} = \frac{1}{1} = 1$;

Производная функции:
$y'(x) = \frac{(x^2 + 1)’ \cdot (x^2 — 1) — (x^2 + 1) \cdot (x^2 — 1)’}{(x^2 — 1)^2}$;
$y'(x) = \frac{2x \cdot (x^2 — 1) — (x^2 + 1) \cdot 2x}{(x^2 — 1)^2}$;
$y'(x) = \frac{2x^3 — 2x — 2x^3 — 2x}{(x^2 — 1)^2} = \frac{-4x}{(x^2 — 1)^2}$;

Промежуток возрастания:
$-4x \geq 0$;
$x \leq 0$;
$x = 0$ — точка максимума;
$y_{\max} = \frac{0^2 + 1}{0^2 — 1} = \frac{1}{-1} = -1$;

График функции:

а) $y = \dfrac{x^2 + 4}{x^2 — 4}$

1) Область определения функции

Функция — это дробь:

$$y = \dfrac{x^2 + 4}{x^2 — 4}$$

Чтобы дробь была определена, знаменатель не должен быть равен нулю:

$$x^2 — 4 \neq 0 \Rightarrow x^2 \neq 4 \Rightarrow x \neq \pm2$$

Вывод:

$$D(y) = (-\infty; -2) \cup (-2; 2) \cup (2; +\infty)$$

2) Чётность функции

Проверим, является ли функция чётной, нечётной или ни той, ни другой.

Подставим $-x$ вместо $x$:

$$y(-x) = \dfrac{(-x)^2 + 4}{(-x)^2 — 4} = \dfrac{x^2 + 4}{x^2 — 4} = y(x)$$

Так как $y(-x) = y(x)$, функция чётная.

Вывод:
Функция чётная ⇒ график симметричен относительно оси $Oy$.

3) Асимптоты функции

Вертикальные асимптоты

Функция не определена в точках, где знаменатель равен нулю:

$$x^2 — 4 = 0 \Rightarrow x = \pm2$$

Ответ: вертикальные асимптоты:

$$x = -2, \quad x = 2$$

Горизонтальная асимптота

Для $x \to \pm\infty$ поведение функции определяется отношением старших степеней числителя и знаменателя:

$$y = \dfrac{x^2 + 4}{x^2 — 4}$$

Доминирующие члены: числитель — $x^2$, знаменатель — $x^2$

Разделим числитель и знаменатель на $x^2$:

$$\lim_{x \to \infty} \dfrac{1 + \frac{4}{x^2}}{1 — \frac{4}{x^2}} = \dfrac{1 + 0}{1 — 0} = 1$$

Ответ: горизонтальная асимптота:

$$y = 1$$

4) Производная функции

Используем правило дифференцирования дроби:

$$y = \dfrac{u}{v}, \quad y’ = \dfrac{u’v — uv’}{v^2}$$

Где:

• $u = x^2 + 4$, тогда $u’ = 2x$
• $v = x^2 — 4$, тогда $v’ = 2x$

Подставим:

$$y'(x) = \dfrac{2x(x^2 — 4) — 2x(x^2 + 4)}{(x^2 — 4)^2}$$

Раскроем скобки в числителе:

$$2x(x^2 — 4) = 2x^3 — 8x \\ 2x(x^2 + 4) = 2x^3 + 8x$$

Теперь:

$$y'(x) = \dfrac{(2x^3 — 8x) — (2x^3 + 8x)}{(x^2 — 4)^2} = \dfrac{2x^3 — 8x — 2x^3 — 8x}{(x^2 — 4)^2} = \dfrac{-16x}{(x^2 — 4)^2}$$

5) Промежутки возрастания и убывания

Производная:

$$y'(x) = \dfrac{-16x}{(x^2 — 4)^2}$$

Знаменатель $(x^2 — 4)^2 > 0$ при всех $x \neq \pm 2$

Знак производной определяется только по числителю $-16x$:

• $-16x > 0 \Rightarrow x < 0 \Rightarrow$ функция возрастает
• $-16x < 0 \Rightarrow x > 0 \Rightarrow$ функция убывает

Вывод:

• Функция возрастает на $(-\infty; -2) \cup (-2; 0)$
• Функция убывает на $(0; 2) \cup (2; +\infty)$

6) Точки экстремума

Критическая точка:

$$y'(x) = 0 \Rightarrow -16x = 0 \Rightarrow x = 0$$

Это внутренняя точка области определения.

Вычислим значение функции в этой точке:

$$y(0) = \dfrac{0^2 + 4}{0^2 — 4} = \dfrac{4}{-4} = -1$$

Так как производная меняет знак с положительного на отрицательный при переходе через 0, это точка максимума.

Ответ:

• Точка максимума: $x = 0$
• Значение: $y_{\max} = -1$

7) График функции — словесное описание

• График разрывный в точках $x = \pm 2$ — вертикальные асимптоты
• Имеет горизонтальную асимптоту $y = 1$
• Симметричен относительно оси $Oy$ (чётная функция)
• Максимум в точке $(0, -1)$
• На промежутках $(-\infty; -2)$ и $(-2; 0)$ функция возрастает
• На промежутках $(0; 2)$ и $(2; +\infty)$ функция убывает

б) $y = \dfrac{x^2 + 1}{x^2 — 1}$

1) Область определения функции

Функция:

$$y = \dfrac{x^2 + 1}{x^2 — 1}$$

Определена, если знаменатель $x^2 — 1 \neq 0$:

$$x^2 — 1 \neq 0 \Rightarrow x^2 \neq 1 \Rightarrow x \neq \pm 1$$

Ответ:

$$D(y) = (-\infty; -1) \cup (-1; 1) \cup (1; +\infty)$$

2) Чётность функции

Подставим $-x$:

$$y(-x) = \dfrac{(-x)^2 + 1}{(-x)^2 — 1} = \dfrac{x^2 + 1}{x^2 — 1} = y(x)$$

Функция чётная ⇒ график симметричен относительно оси $Oy$

3) Асимптоты

Вертикальные асимптоты:

$$x = \pm 1$$

Горизонтальная асимптота:

Рассматриваем предел при $x \to \pm\infty$:

$$\lim_{x \to \infty} \dfrac{x^2 + 1}{x^2 — 1} = \dfrac{1 + \frac{1}{x^2}}{1 — \frac{1}{x^2}} \to \dfrac{1 + 0}{1 — 0} = 1$$

Ответ: горизонтальная асимптота: $y = 1$

4) Производная функции

Применяем правило производной дроби:

• $u = x^2 + 1 \Rightarrow u’ = 2x$
• $v = x^2 — 1 \Rightarrow v’ = 2x$

$$y'(x) = \dfrac{2x(x^2 — 1) — 2x(x^2 + 1)}{(x^2 — 1)^2}$$

Вычислим:

• $2x(x^2 — 1) = 2x^3 — 2x$
• $2x(x^2 + 1) = 2x^3 + 2x$

$$y'(x) = \dfrac{2x^3 — 2x — 2x^3 — 2x}{(x^2 — 1)^2} = \dfrac{-4x}{(x^2 — 1)^2}$$

5) Промежутки возрастания и убывания

Знаменатель $(x^2 — 1)^2 > 0$ при $x \neq \pm1$

Знак производной зависит от числителя $-4x$:

• $x < 0 \Rightarrow -4x > 0 \Rightarrow$ функция возрастает
• $x > 0 \Rightarrow -4x < 0 \Rightarrow$ функция убывает

Ответ:

• Возрастает: $(-\infty; -1) \cup (-1; 0)$
• Убывает: $(0; 1) \cup (1; +\infty)$

6) Точка экстремума

Производная равна нулю при $x = 0$

Проверим значение функции:

$$y(0) = \dfrac{0^2 + 1}{0^2 — 1} = \dfrac{1}{-1} = -1$$

Знак производной меняется с плюса на минус ⇒ это максимум

Ответ:

• Точка максимума: $x = 0$
• Значение: $y_{\max} = -1$

7) График функции — словесное описание

• Разрывы в точках $x = \pm 1$ — вертикальные асимптоты
• Горизонтальная асимптота: $y = 1$
• Чётная функция ⇒ симметрия относительно оси $Oy$
• Максимум в точке $(0, -1)$
• Возрастает на $(-\infty; -1) \cup (-1; 0)$
• Убывает на $(0; 1) \cup (1; +\infty)$