ГДЗ 10-11 Класс Номер 31.14 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

а) Постройте график функции $y=-x^4+2x^2+8$.

б) При каких значениях параметра а уравнение $-x^4+2x^2+8=a$ не имеет корней?

а) Построим график функции $y = -x^4 + 2x^2 + 8$;

Область определения функции:
$D(y) = (-\infty; +\infty)$;

Функция является четной:
$y(-x) = -(-x)^4 + 2(-x)^2 + 8 = -x^4 + 2x^2 + 8 = y(x)$;

Производная функции:
$y'(x) = -(x^4)’ + 2(x^2)’ + (8)’ = -4x^3 + 2 \cdot 2x + 0 = 4x — 4x^3$;

Промежуток возрастания:
$4x — 4x^3 \geq 0$;
$4x^3 — 4x \leq 0$;
$4x(x^2 — 1) \leq 0$;
$(x + 1)x(x — 1) \leq 0$;
$x \leq -1$ или $0 \leq x \leq 1$;
$x = 0$ — точка минимума;
$x = \pm 1$ — точки максимума;
$y_{\min} = -0^4 + 2 \cdot 0^2 + 8 = 8$;
$y_{\max} = -(\pm 1)^4 + 2 \cdot (\pm 1)^2 + 8 = -1 + 2 + 8 = 9$;

Координаты некоторых точек:

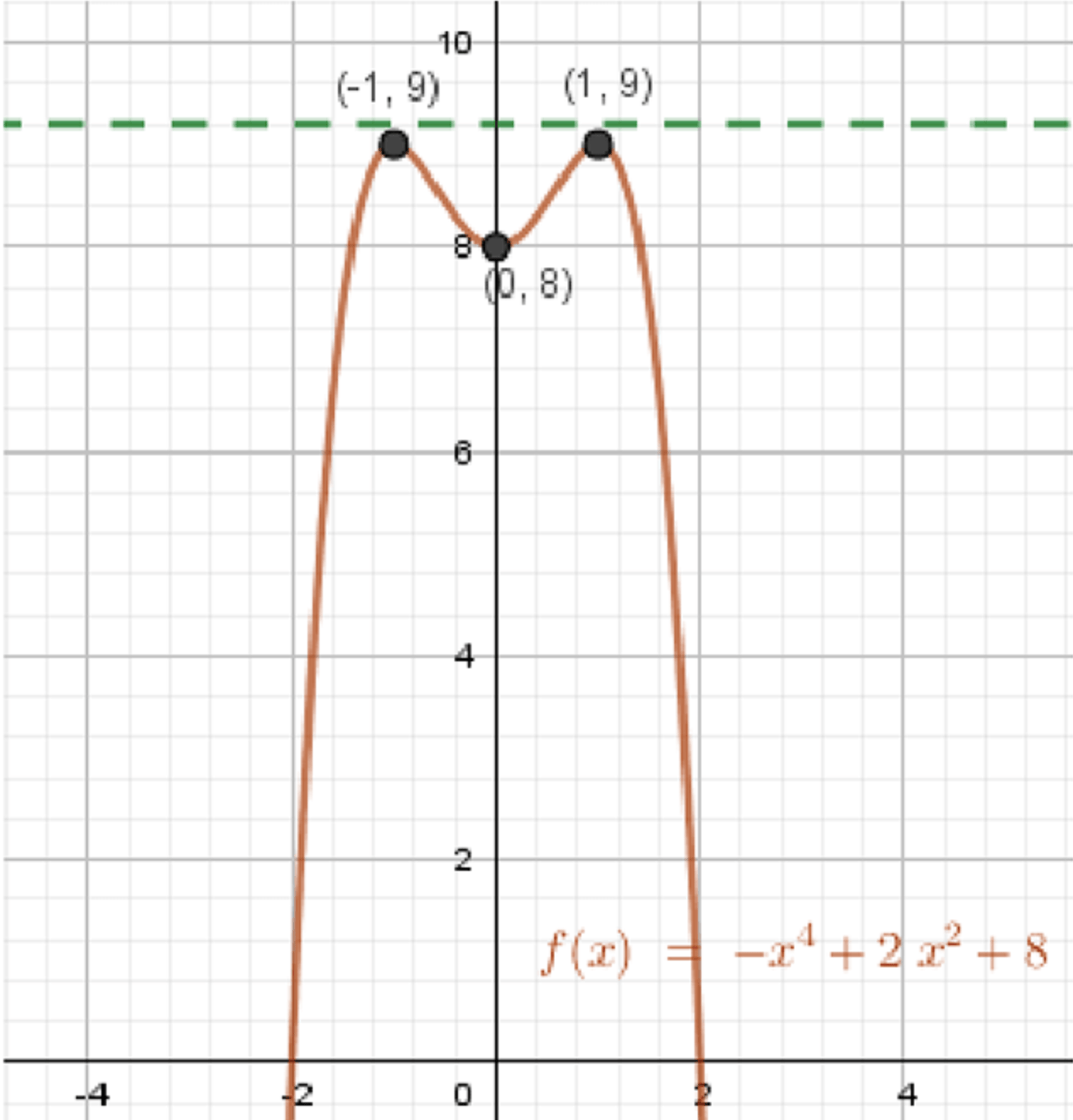
График функции:

б) Уравнение $-x^4 + 2x^2 + 8 = a$ не имеет корней при $a > 9$.

а) Построим график функции $y = -x^4 + 2x^2 + 8$

1) Область определения функции

Функция является многочленом четвёртой степени.
Многочлены определены при всех значениях $x \in \mathbb{R}$, поэтому:

$$D(y) = (-\infty; +\infty)$$

2) Чётность функции

Чтобы определить, является ли функция чётной, вычислим $y(-x)$:

$$y(-x) = -(-x)^4 + 2(-x)^2 + 8 = -x^4 + 2x^2 + 8 = y(x)$$

Так как $y(-x) = y(x)$, функция — чётная.

Вывод: график симметричен относительно оси $Oy$.

3) Производная функции

Найдём первую производную:

$$y(x) = -x^4 + 2x^2 + 8 \Rightarrow y'(x) = (-x^4)’ + (2x^2)’ + (8)’ = -4x^3 + 4x$$

Приведём к удобному виду:

$$y'(x) = 4x — 4x^3$$

Найдём критические точки

Приравниваем производную к нулю:

$$y'(x) = 4x — 4x^3 = 0 \Rightarrow 4x(1 — x^2) = 0 \Rightarrow 4x(x — 1)(x + 1) = 0$$

Нули производной:

$$x = -1, \quad x = 0, \quad x = 1$$

4) Исследование на возрастание и убывание

Знаки производной зависят от выражения:

$$y'(x) = 4x(1 — x^2) = 4x(-x^2 + 1) = 4x(x + 1)(x — 1)$$

Построим таблицу знаков:

Рассмотрим промежутки: $(-\infty, -1)$, $(-1, 0)$, $(0, 1)$, $(1, +\infty)$

• $x < -1$:
  • $x < 0 \Rightarrow 4x < 0$
  • $x + 1 < 0$
  • $x — 1 < 0$
    ⇒ знак: $(-)(-)(-) = —$
• $-1 < x < 0$:
  • $4x < 0$
  • $x + 1 > 0$
  • $x — 1 < 0$
    ⇒ знак: $(-)(+)(-) = +$
• $0 < x < 1$:
  • $4x > 0$
  • $x + 1 > 0$
  • $x — 1 < 0$
    ⇒ знак: $(+)(+)(-) = —$
• $x > 1$:
  • $4x > 0$
  • $x + 1 > 0$
  • $x — 1 > 0$
    ⇒ знак: $(+)(+)(+) = +$

Вывод:

5) Точки экстремума

1. $x = -1$

• Слева: производная отрицательная
• Справа: производная положительная
  ⇒ минимум

$$y(-1) = -(-1)^4 + 2(-1)^2 + 8 = -1 + 2 + 8 = 9$$

2. $x = 0$

• Слева: производная положительная
• Справа: производная отрицательная
  ⇒ максимум

$$y(0) = -0^4 + 2 \cdot 0^2 + 8 = 8$$

3. $x = 1$

• Слева: производная отрицательная
• Справа: производная положительная
  ⇒ минимум

$$y(1) = -1^4 + 2 \cdot 1^2 + 8 = -1 + 2 + 8 = 9$$

6) Точки пересечения с осями координат

Ось $Oy$

Подставим $x = 0$:

$$y = -0^4 + 2 \cdot 0^2 + 8 = 8 \Rightarrow (0, 8)$$

Ось $Ox$

Решим уравнение $y = 0$:

$$-x^4 + 2x^2 + 8 = 0 \Rightarrow x^4 — 2x^2 — 8 = 0$$

Введём замену: $t = x^2$:

$$t^2 — 2t — 8 = 0 \Rightarrow D = (-2)^2 + 4 \cdot 1 \cdot 8 = 4 + 32 = 36$$ $$t_{1,2} = \dfrac{2 \pm \sqrt{36}}{2} = \dfrac{2 \pm 6}{2} \Rightarrow t_1 = 4, \quad t_2 = -2$$

Т.к. $t = x^2 \geq 0$, $t = -2$ — не подходит.

$$x^2 = 4 \Rightarrow x = \pm 2 \Rightarrow \text{точки пересечения с осью } Ox: \quad (-2, 0), \quad (2, 0)$$

7) Значения функции в некоторых точках

8) График функции — словесное описание

• Чётная функция, симметрия относительно оси $Oy$
• Максимум в точке $(0, 8)$
• Минимумы в точках $(-1, 9)$ и $(1, 9)$
• Функция убывает на $(-\infty, -1)$, возрастает на $(-1, 0)$, убывает на $(0, 1)$, возрастает на $(1, +\infty)$
• Пересекает ось $Ox$ в точках $(-2, 0)$ и $(2, 0)$
• Пересекает ось $Oy$ в точке $(0, 8)$
• Форма графика — перевёрнутая буква «М», вершины которой находятся в точках $x = \pm 1$, минимум в центре $x = 0$

б) Уравнение $-x^4 + 2x^2 + 8 = a$ не имеет корней при $a > 9$

Рассмотрим уравнение:

$$-x^4 + 2x^2 + 8 = a \Rightarrow -x^4 + 2x^2 + (8 — a) = 0$$

Перепишем:

$$x^4 — 2x^2 + (a — 8) = 0$$

Введём замену $t = x^2$, тогда $t \geq 0$, и уравнение примет вид:

$$t^2 — 2t + (a — 8) = 0$$

Найдём условие, при котором уравнение не имеет корней по $x$:

Функция $y = -x^4 + 2x^2 + 8$ достигает максимального значения в точках $x = \pm 1$:

$$y_{\max} = 9$$

Значит, если $a > 9$, уравнение

$$-x^4 + 2x^2 + 8 = a$$

не имеет решений, так как значение левой части не может быть больше 9 при любом $x$.

Вывод:

• Уравнение не имеет действительных корней при $a > 9$, потому что функция не достигает таких значений.