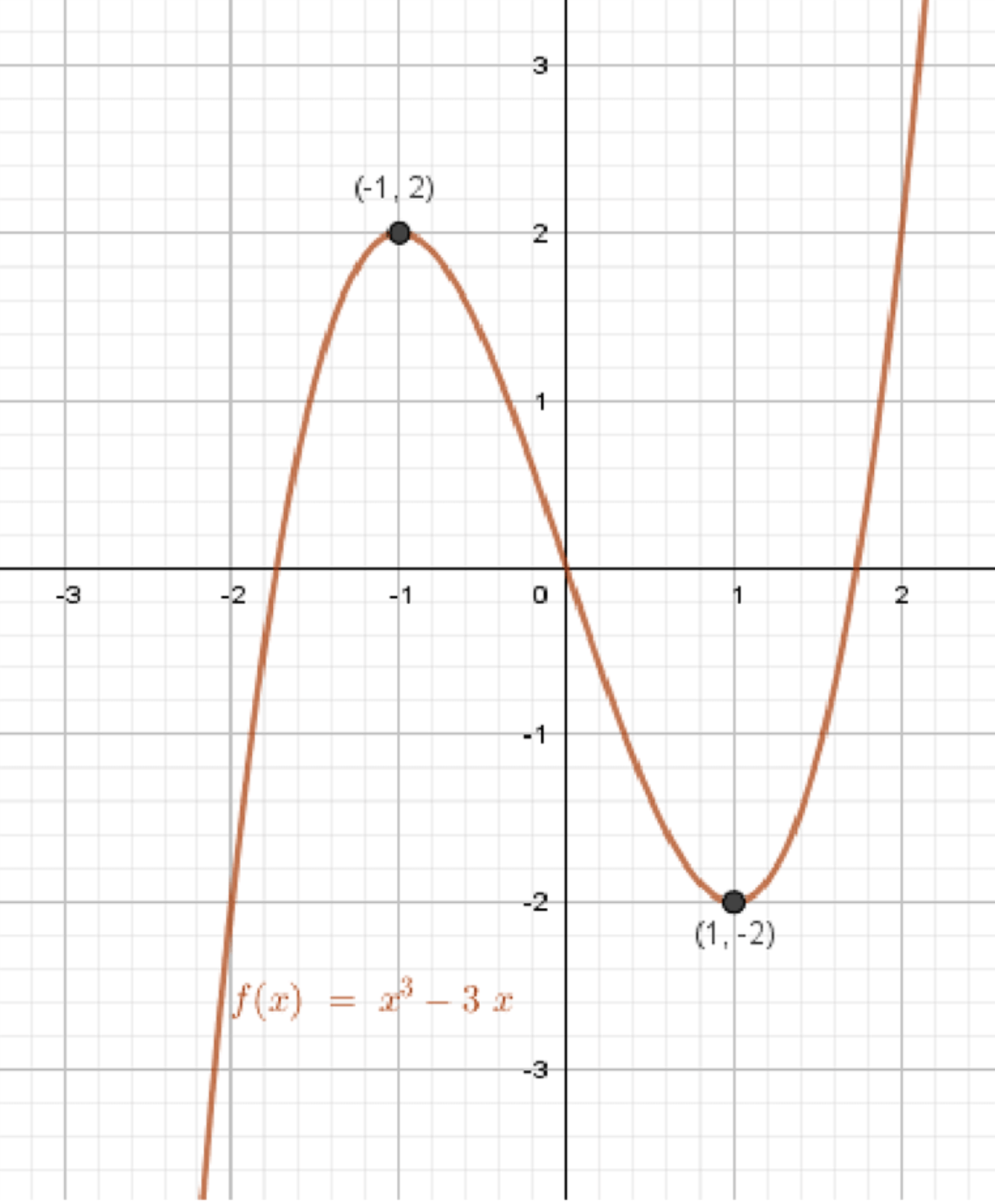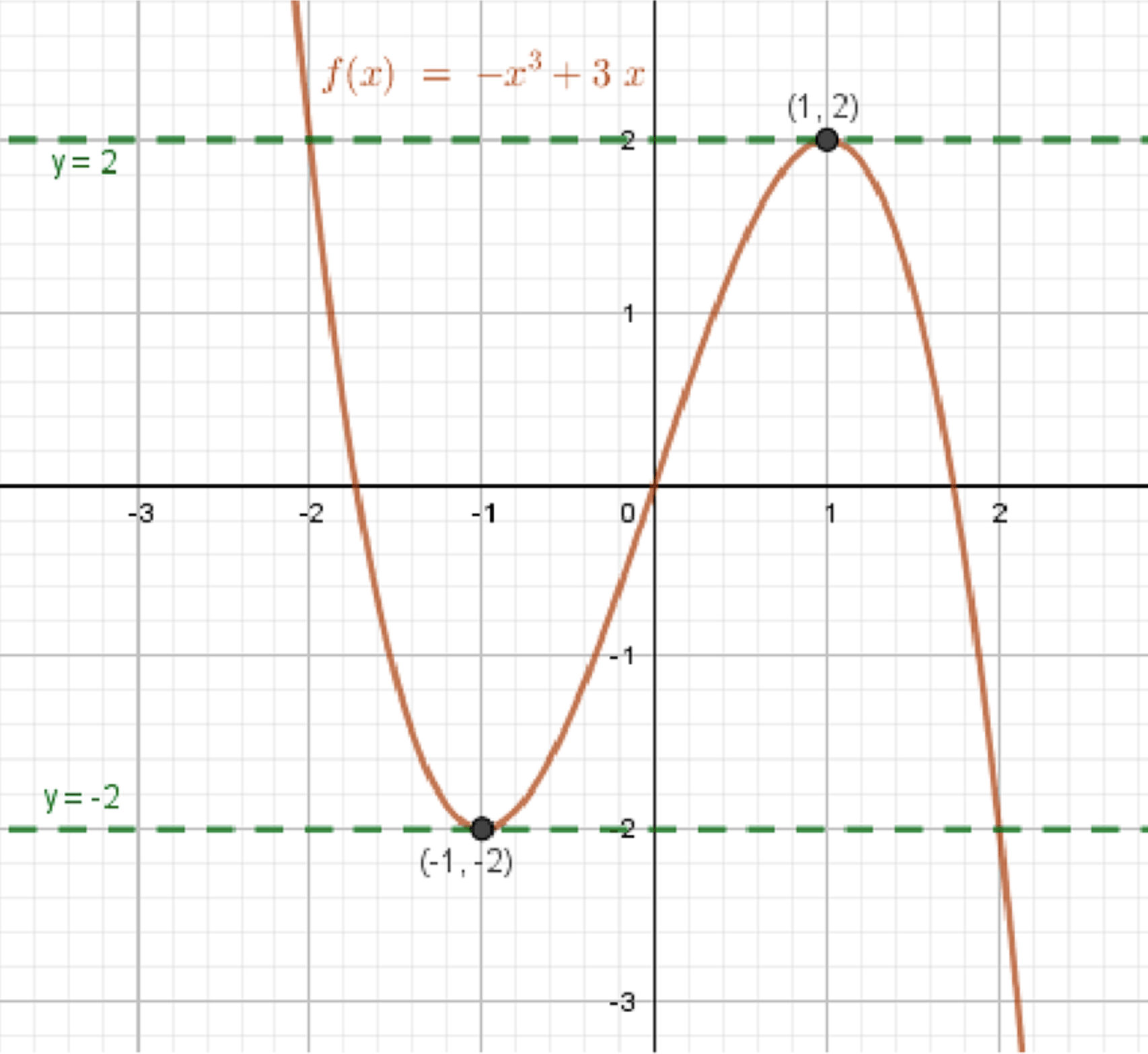ГДЗ 10-11 Класс Номер 31.15 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

При каких значениях параметра а:

а) уравнение x³ — 3х = а имеет один корень;

б) уравнение 3x — x³ = a имеет два корня?

При каких значениях параметра $a$:

а) Уравнение $x^3 — 3x = a$ имеет один корень:
$f(x) = x^3 — 3x$;

Область определения функции:
$D(f) = (-\infty; +\infty)$;

Функция является нечетной:
$f(-x) = (-x)^3 — 3(-x) = -x^3 + 3x = -f(x)$;

Производная функции:
$f'(x) = (x^3)’ — (3x)’ = 3x^2 — 3$;

Промежуток возрастания:
$3x^2 — 3 \geq 0$;
$x^2 — 1 \geq 0$;
$(x + 1)(x — 1) \geq 0$;
$x \leq -1$ или $x \geq 1$;
$x = 1$ — точка минимума;
$x = -1$ — точка максимума;
$y_{\min} = 1^3 — 3 \cdot 1 = 1 — 3 = -2$;
$y_{\max} = (-1)^3 — 3 \cdot (-1) = -1 + 3 = 2$;

График функции:

Ответ: $a \in (-\infty; -2) \cup (2; +\infty)$.

б) Уравнение $3x — x^3 = a$ имеет два корня:
$f(x) = 3x — x^3$;

Область определения функции:
$D(f) = (-\infty; +\infty)$;

Функция является нечетной:
$f(-x) = 3(-x) — (-x)^3 = -3x + x^3 = -f(x)$;

Производная функции:
$f'(x) = (3x)’ — (x^3)’ = 3 — 3x^2$;

Промежуток возрастания:
$3 — 3x^2 \geq 0$;
$1 — x^2 \geq 0$;
$x^2 — 1 \leq 0$;
$(x + 1)(x — 1) \leq 0$;
$-1 \leq x \leq 1$;
$x = -1$ — точка минимума;
$x = 1$ — точка максимума;
$y_{\min} = 3 \cdot (-1) — (-1)^3 = -3 + 1 = -2$;
$y_{\max} = 3 \cdot 1 — 1^3 = 3 — 1 = 2$;

График функции:

Ответ: $a \in \{-2; 2\}$.

а) Уравнение $x^3 — 3x = a$ имеет один корень

Рассмотрим функцию:

$$f(x) = x^3 — 3x$$

1) Область определения функции

Функция $f(x)$ является многочленом, а многочлены определены на всей числовой прямой.

Вывод:

$$D(f) = (-\infty; +\infty)$$

2) Чётность функции

Проверим, является ли функция чётной или нечётной:

$$f(-x) = (-x)^3 — 3(-x) = -x^3 + 3x = — (x^3 — 3x) = -f(x)$$

Так как $f(-x) = -f(x)$, функция — нечётная.

Вывод: график симметричен относительно начала координат.

3) Производная функции

Найдём первую производную функции:

$$f'(x) = (x^3)’ — (3x)’ = 3x^2 — 3$$

Производная нужна для анализа возрастания и убывания функции.

Найдём критические точки:

Решим уравнение:

$$f'(x) = 3x^2 — 3 = 0 \Rightarrow x^2 = 1 \Rightarrow x = \pm 1$$

Знаки производной на промежутках:

Разобьём числовую прямую на интервалы:

• $(-\infty; -1)$
• $(-1; 1)$
• $(1; +\infty)$

Знаки производной на этих интервалах:

• $x < -1 \Rightarrow f'(x) = 3x^2 — 3 > 0$
• $-1 < x < 1 \Rightarrow f'(x) < 0$
• $x > 1 \Rightarrow f'(x) > 0$

4) Возрастание и убывание

5) Точки экстремума

• $x = -1$: производная меняется с $+$ на $—$ ⇒ максимум

$$f(-1) = (-1)^3 — 3 \cdot (-1) = -1 + 3 = 2$$

• $x = 1$: производная меняется с $—$ на $+$ ⇒ минимум

$$f(1) = 1^3 — 3 \cdot 1 = 1 — 3 = -2$$

6) График и количество корней уравнения

Функция $f(x) = x^3 — 3x$ непрерывна и дифференцируема на $\mathbb{R}$.
График имеет:

• максимум при $x = -1$, $y = 2$
• минимум при $x = 1$, $y = -2$

Таким образом:

• функция достигает всех значений от $-2$ до $2$ трижды
• на промежутках $(-\infty; -2) \cup (2; +\infty)$ функция однозначна (монотонна)

Ответ:

Уравнение имеет один корень, если:

$$a \in (-\infty; -2) \cup (2; +\infty)$$

б) Уравнение $3x — x^3 = a$ имеет два корня

Рассмотрим функцию:

$$f(x) = 3x — x^3$$

1) Область определения функции

Функция — многочлен ⇒ определена на всей числовой прямой:

$$D(f) = (-\infty; +\infty)$$

2) Чётность функции

Проверим:

$$f(-x) = 3(-x) — (-x)^3 = -3x + x^3 = -f(x)$$

Вывод: функция нечётная, график симметричен относительно начала координат.

3) Производная функции

$$f'(x) = (3x)’ — (x^3)’ = 3 — 3x^2$$

Критические точки:

$$f'(x) = 0 \Rightarrow 3 — 3x^2 = 0 \Rightarrow x^2 = 1 \Rightarrow x = \pm 1$$

Знаки производной:

• $x < -1 \Rightarrow f'(x) < 0$
• $-1 < x < 1 \Rightarrow f'(x) > 0$
• $x > 1 \Rightarrow f'(x) < 0$

4) Поведение функции

5) Точки экстремума

• $x = -1$: производная меняется с $—$ на $+$ ⇒ минимум

$$f(-1) = 3 \cdot (-1) — (-1)^3 = -3 + 1 = -2$$

• $x = 1$: производная меняется с $+$ на $—$ ⇒ максимум

$$f(1) = 3 \cdot 1 — 1^3 = 3 — 1 = 2$$

6) Анализ количества корней

График функции:

• достигает значения от $-2$ до $2$
• $f(x) = a$ имеет:
  • три корня, если $a \in (-2; 2)$
  • один корень, если $a < -2$ или $a > 2$
  • два корня, если $a = -2$ или $a = 2$
    (одно значение достигается в двух точках — в экстремумах)

Ответ:

Уравнение имеет два корня, если:

$$a\in \{-2;2\}$$