ГДЗ 10-11 Класс Номер 31.19 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Решить графически уравнение:

а) $3\sqrt{x+1} = -x^3 + 3x^2 + 6$;

$f(x) = 3\sqrt{x+1}$:
Область определения:
$x + 1 \geq 0$;
$x \geq -1$;

Производная функции:
$f'(x) = 3 \cdot \frac{1}{2\sqrt{x+1}} = \frac{3}{2\sqrt{x+1}} > 0$;
Функция возрастает на всей области определения;

$$\begin{array}{|c|c|c|c|c|} \hline x & -1 & 0 & 3 & 8 \\ \hline y & 0 & 3 & 6 & 9 \\ \hline \end{array}$$

$g(x) = -x^3 + 3x^2 + 6$;
Область определения:
$x \in R$;

Производная функции:
$g'(x) = -(x^3)’ + 3(x^2)’ + (6)’$;
$g'(x) = -3x^2 + 3 \cdot 2x + 0 = 6x — 3x^2$;

Промежуток возрастания:
$6x — 3x^2 \geq 0$;
$3x^2 — 6x \leq 0$;
$3x(x — 2) \leq 0$;
$0 \leq x \leq 2$;

$$\begin{array}{|c|c|c|c|c|} \hline x & -1 & 0 & 2 & 3 \\ \hline y & 10 & 6 & 10 & 6 \\ \hline \end{array}$$

Графики функций:

Ответ: $x = 3$.

б) $x^3 — 3x = (x + 1)^6 + 2$;

$f(x) = x^3 — 3x$:
Область определения:
$x \in R$;

Производная функции:
$f'(x) = (x^3)’ — (3x)’ = 3x^2 — 3$;

Промежуток возрастания:
$3x^2 — 3 \geq 0$;
$x^2 — 1 \geq 0$;
$(x + 1)(x — 1) \geq 0$;
$x \leq -1$ или $x \geq 1$;

$$\begin{array}{|c|c|c|c|c|} \hline x & -2 & -1 & 1 & 2 \\ \hline y & -2 & 2 & -2 & 2 \\ \hline \end{array}$$

$g(x) = (x + 1)^6 + 2$;
Область определения:
$x \in R$;

Производная функции:
$g'(x) = 1 \cdot 6(x + 1)^5 + 0 = 6(x + 1)^5$;

Промежуток возрастания:
$6(x + 1)^5 \geq 0$;
$x + 1 \geq 0$;
$x \geq -1$;

$$\begin{array}{|c|c|c|c|} \hline x & -2 & -1 & 0 \\ \hline y & 3 & 2 & 3 \\ \hline \end{array}$$

Графики функций:

Ответ: $x = -1$.

а)

Решить уравнение:

$$3\sqrt{x+1} = -x^3 + 3x^2 + 6$$

1. Исследуем левую часть:

$$f(x) = 3\sqrt{x+1}$$

1.1 Область определения:

Подкоренное выражение должно быть неотрицательным:

$$x + 1 \geq 0 \Rightarrow x \geq -1$$

То есть:

$$D(f) = [-1; +\infty)$$

1.2 Производная:

$$f(x) = 3\sqrt{x + 1} = 3(x + 1)^{1/2}$$ $$f'(x) = 3 \cdot \frac{1}{2\sqrt{x+1}} = \frac{3}{2\sqrt{x+1}}$$

Так как $\sqrt{x+1} > 0$ при $x > -1$, то:

$$f'(x) > 0 \Rightarrow f(x) \text{ возрастает на } (-1; +\infty)$$

1.3 Таблица значений:

2. Исследуем правую часть:

$$g(x) = -x^3 + 3x^2 + 6$$

2.1 Область определения:

Полином определён на всей числовой прямой:

$$D(g) = (-\infty; +\infty)$$

2.2 Производная:

$$g'(x) = \frac{d}{dx}(-x^3 + 3x^2 + 6) = -3x^2 + 6x$$ $$g'(x) = -3x^2 + 6x = 3x(-x + 2)$$

2.3 Исследуем знак производной:

$$g'(x) \geq 0 \Rightarrow 3x(2 — x) \geq 0$$

Решаем неравенство:

$$x \in [0; 2]$$

Значит:

• $g(x)$ возрастает на $[0; 2]$
• убывает на $(-\infty; 0) \cup (2; +\infty)$

2.4 Таблица значений:

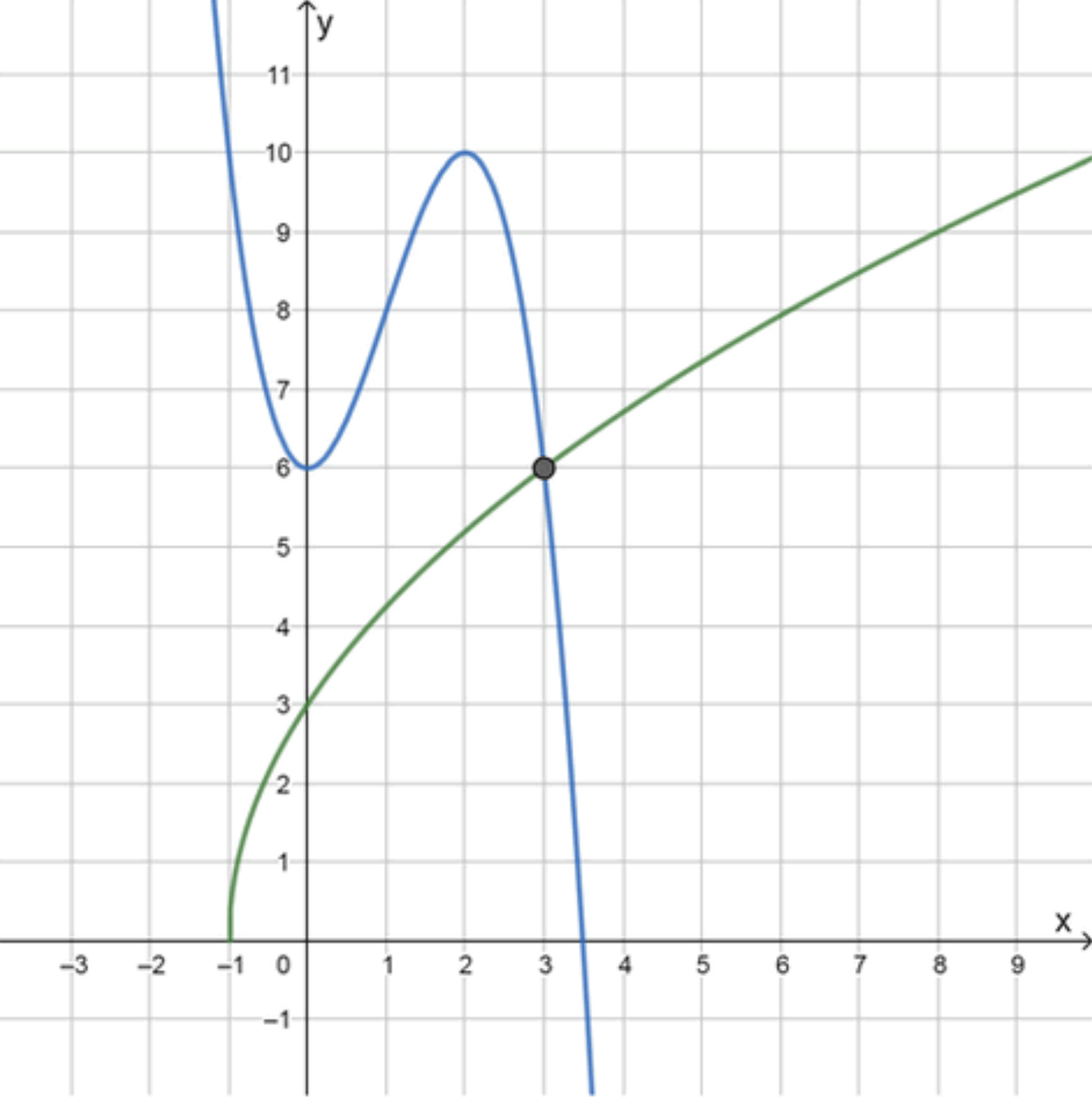
3. Сравниваем графики:

Ищем пересечение графиков $f(x) = 3\sqrt{x+1}$ и $g(x) = -x^3 + 3x^2 + 6$

Из таблиц значений:

$$f(3) = 6, \quad g(3) = 6 \Rightarrow f(3) = g(3)$$

Ответ:

$$\boxed{x = 3}$$

б)

Решить уравнение:

$$x^3 — 3x = (x + 1)^6 + 2$$

1. Левая часть:

$$f(x) = x^3 — 3x$$

1.1 Область определения:

$$D(f) = (-\infty; +\infty)$$

1.2 Производная:

$$f'(x) = 3x^2 — 3 = 3(x^2 — 1)$$

Решаем:

$$f'(x) \geq 0 \Rightarrow x^2 — 1 \geq 0 \Rightarrow x \leq -1 \text{ или } x \geq 1$$

• Функция убывает на $(-1; 1)$
• Возрастает на $(-\infty; -1] \cup [1; +\infty)$

1.3 Таблица значений:

2. Правая часть:

$$g(x) = (x + 1)^6 + 2$$

2.1 Область определения:

$$D(g) = (-\infty; +\infty)$$

2.2 Производная:

$$g'(x) = 6(x + 1)^5$$

Знак производной:

• $g'(x) \geq 0$ всегда
• Равна нулю только при $x = -1$

Значит:

• Убывание на $(-\infty; -1)$
• Минимум в точке $x = -1$
• Возрастание на $(-1; +\infty)$

2.3 Таблица значений:

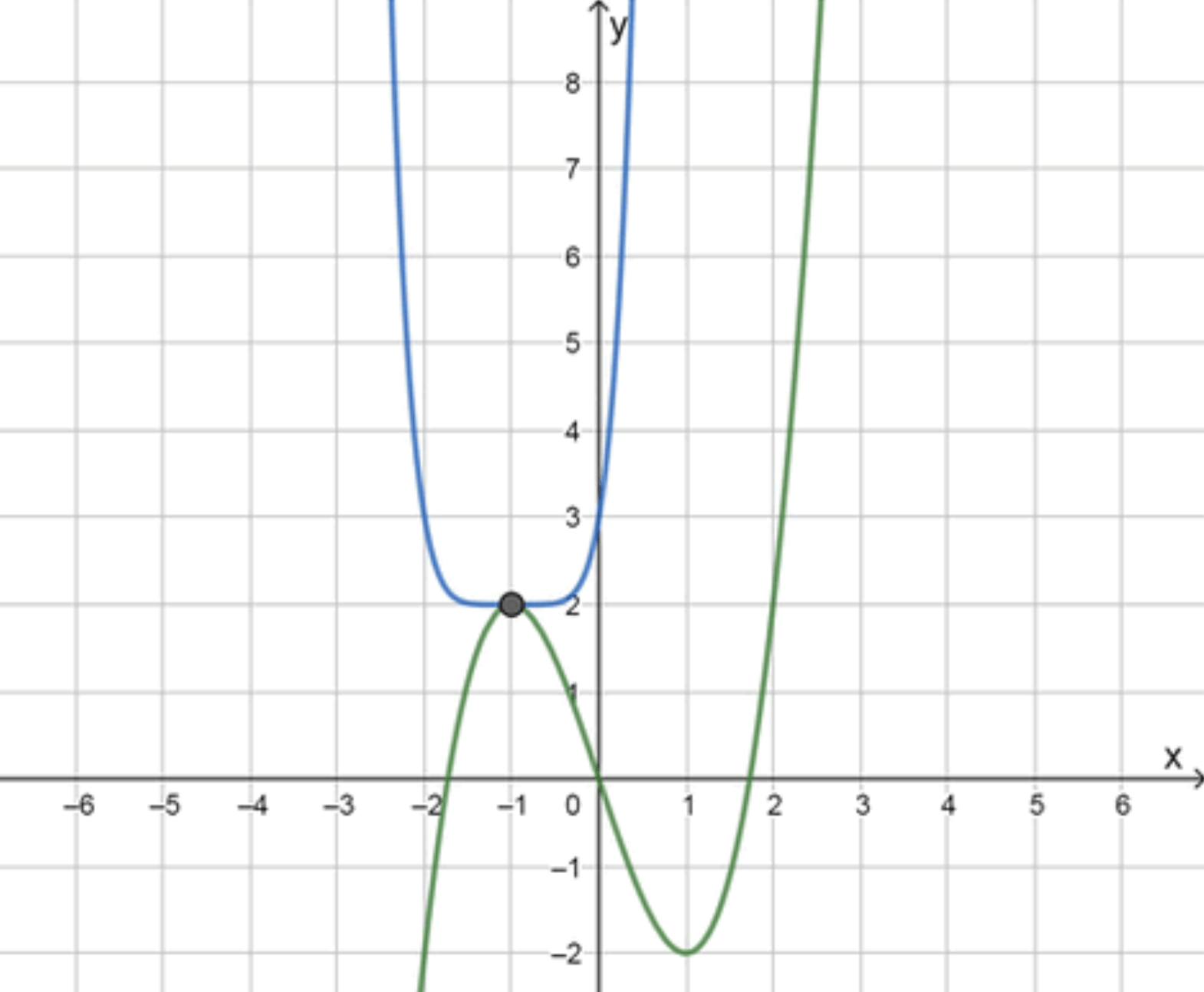
3. Сравниваем графики:

Проверим точку $x = -1$:

• Левая часть:

  $$f(-1) = (-1)^3 — 3 \cdot (-1) = -1 + 3 = 2$$

• Правая часть:

  $$g(-1) = (0)^6 + 2 = 2$$

$$f(-1) = g(-1)$$

Ответ:

$$\boxed{{\displaystyle x=-1}}$$