ГДЗ 10-11 Класс Номер 31.2 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

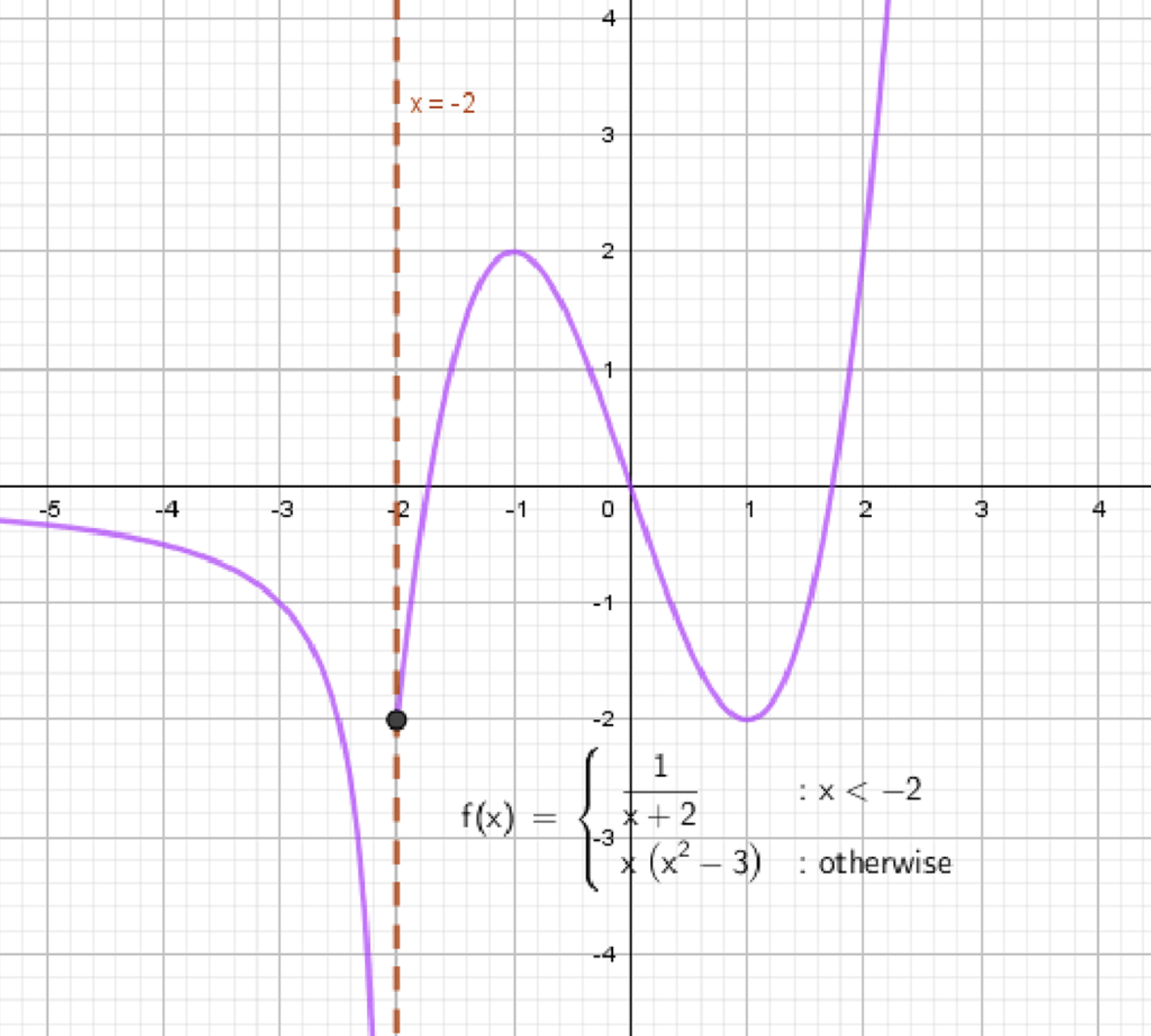
а) Функция имеет разрыв в точке х = -2, максимум в точке х = -1 и минимум в точке х = 1;

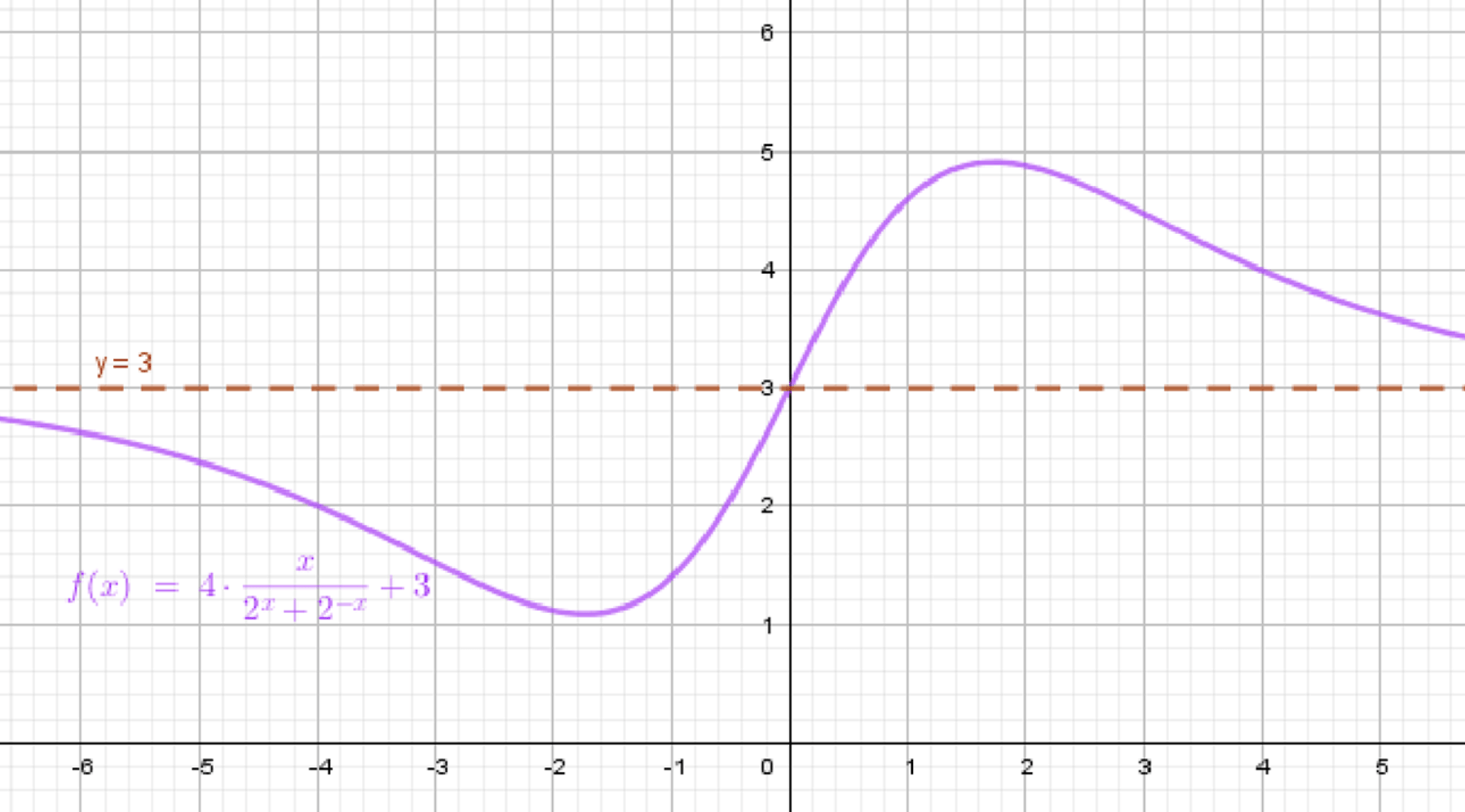
б) функция имеет горизонтальную асимптоту у = 3 при $x\to \mathrm{\infty }$ бесконечность, одну точку максимума и одну точку минимума.

Построить эскиз графика какой-нибудь функции, обладающей указанными свойствами:

а) Функция имеет разрыв в точке $x = -2$, максимум в точке $x = -1$ и минимум в точке $x = 1$:

б) Функция имеет горизонтальную асимптоту $y = 3$ при $x \to \infty$, одну точку максимума и одну точку минимума:

а) Функция имеет разрыв в точке $x = -2$, максимум в точке $x = -1$, минимум в точке $x = 1$

Шаг 1. Разрыв в точке $x = -2$

• Это может быть разрыв первого рода (функция стремится к разным значениям слева и справа) или второго рода (бесконечный скачок).
• Для простоты представим разрыв первого рода: например, с одной стороны график «обрывается», а с другой «поднимается» — точка отсутствует.

Шаг 2. Поведение в точке $x = -1$

• Максимум:
  Значит, в $x = -1$ — вершина, где функция переходит от возрастания к убыванию.

Шаг 3. Поведение в точке $x = 1$

• Минимум:
  Значит, в $x = 1$ — впадина, где функция переходит от убывания к возрастанию.

Шаг 4. Общая структура графика

1. До точки $x = -2$: можно нарисовать какой-то кусок функции, например возрастающий.
2. В точке $x = -2$: разрыв — график обрывается, точка пустая (выколотая).
3. После $x = -2$ — начинаем другой кусок, например продолжается поведение, ведущее к максимуму.
4. В $x = -1$ — максимум.
5. Потом график убывает до $x = 1$ (там минимум).
6. После 1 — график опять начинает возрастать.

Как строить по шагам:

1. Нарисуй оси $x$ и $y$.
2. Поставь выколотую точку в $x = -2$, где будет разрыв.
3. До $x = -2$ нарисуй плавную линию — например, возрастающую.
4. После $x = -2$ — нарисуй другую линию, немного выше или ниже, чтобы показать разрыв.
5. Нарисуй максимум в $x = -1$: вверх — затем спуск.
6. Спуск продолжается до $x = 1$, где минимум.
7. После $x = 1$ — функция снова возрастает.

Как будет выглядеть график:

б) Функция имеет горизонтальную асимптоту $y = 3$ при $x \to \infty$, одну точку максимума и одну точку минимума

Шаг 1. Горизонтальная асимптота

• $y = 3$ — прямая, к которой график приближается при $x \to +\infty$, но никогда не пересекает её (или только при особых условиях).
• Это значит: значение функции «стабилизируется» около 3 справа.

Шаг 2. Максимум и минимум

• Одна точка максимума и одна точка минимума — график должен сначала подняться до пика (макс), затем опуститься в яму (мин), и после этого — возможно, стабилизироваться.

Возможная форма функции:

• Подойдёт рациональная функция, например:

$$y = \frac{(x — a)(x — b)}{x + 1} + 3$$

где $a < b$, а знаменатель обеспечивает асимптоту.

Но мы не ищем формулу, а рисуем форму графика по поведению.

Как строить:

1. Нарисуй горизонтальную пунктирную прямую $y = 3$ (асимптота).
2. Построй точку максимума — например, в $x = 0$, отметь как вершину.
3. Далее спуск к минимуму — например, в $x = 2$.
4. После минимума график начинает подниматься и приближается к $y = 3$, но не пересекает её.

Визуально график будет выглядеть так: