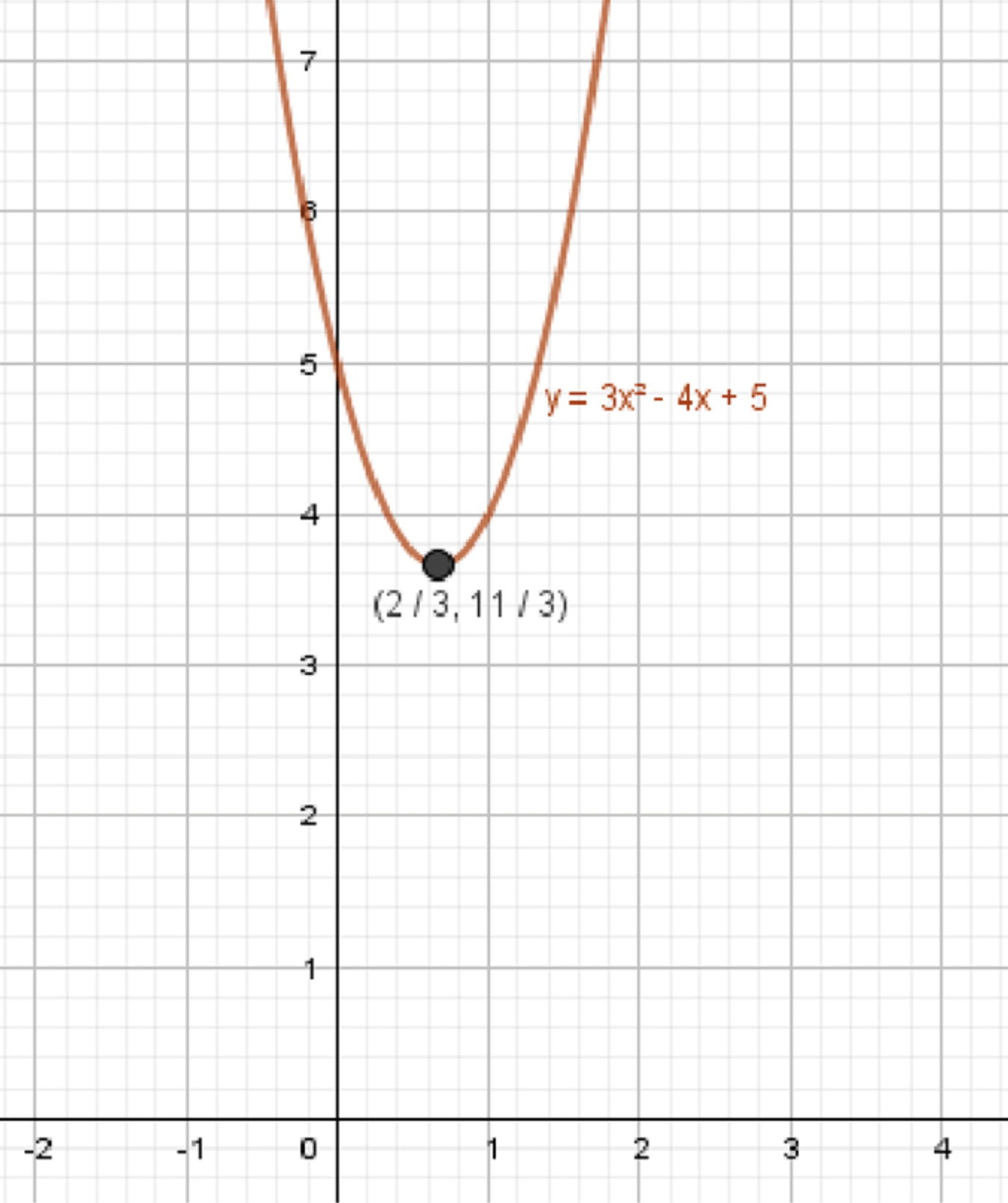ГДЗ 10-11 Класс Номер 31.3 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Исследуйте функцию и постройте её график:

а) $y = 3x^2 — 4x + 5$;

б) $y = 3 + 2x — x^2$;

в) $y = 7 — x — 2x^2$;

г) $y = 5x^2 — 15x — 4$

Исследовать функцию и построить ее график:

а) $y = 3x^2 — 4x + 5$;

Область определения функции:
$D(y) = (-\infty; +\infty)$;

Функция не является ни четной, ни нечетной:
$y(-x) = 3(-x)^2 — 4(-x) + 5 = 3x^2 + 4x + 5$;

У функции отсутствуют асимптоты;

Производная функции:
$y'(x) = 3(x^2)’ + (-4x + 5)’ = 3 \cdot 2x — 4 = 6x — 4$;

Промежуток возрастания:
$6x — 4 \geq 0$;
$6x \geq 4$;
$x \geq \frac{2}{3}$;
$x = \frac{2}{3}$ — точка минимума;

$y_{\min} = 3 \cdot \left(\frac{2}{3}\right)^2 — 4 \cdot \frac{2}{3} + 5 = \frac{4}{3} — \frac{8}{3} + 5 = \frac{3}{3}$;

Функция возрастает на $\left[\frac{2}{3}; +\infty\right)$ и убывает на $\left(-\infty; \frac{2}{3}\right]$;

Координаты некоторых точек:

График функции:

б) $y = 3 + 2x — x^2$;

Область определения функции:
$D(y) = (-\infty; +\infty)$;

Функция не является ни четной, ни нечетной:
$y(-x) = 3 + 2(-x) — (-x)^2 = 3 — 2x — x^2$;

У функции отсутствуют асимптоты;

Производная функции:
$y'(x) = (3 + 2x)’ — (x^2)’ = 2 — 2x$;

Промежуток возрастания:
$2 — 2x \geq 0$;
$2x \leq 2$;
$x \leq 1$;
$x = 1$ — точка максимума;

$y_{\max} = 3 + 2 \cdot 1 — 1^2 = 3 + 2 — 1 = 4$;

Функция возрастает на $(-\infty; 1]$ и убывает на $[1; +\infty)$;

Координаты некоторых точек:

График функции:

в) $y = 7 — x — 2x^2$;

Область определения функции:
$D(y) = (-\infty; +\infty)$;

Функция не является ни четной, ни нечетной:
$y(-x) = 7 — (-x) — 2(-x)^2 = 7 + x — 2x^2$;

У функции отсутствуют асимптоты;

Производная функции:
$y'(x) = (7 — x)’ — 2(x^2)’ = -1 — 4x$;

Промежуток возрастания:
$-1 — 4x \geq 0$;
$-4x \leq 1$;
$x \leq -0{,}25$;
$x = -0{,}25$ — точка максимума;

$y_{\max} = 7 — (-0{,}25) — 2(-0{,}25)^2 = 7 + 0{,}25 — 0{,}125 = 7{,}125$;

Функция возрастает на $(-\infty; -0{,}25]$ и убывает на $[-0{,}25; +\infty)$;

Координаты некоторых точек:

График функции:

г) $y = 5x^2 — 15x — 4$;

Область определения функции:
$D(y) = (-\infty; +\infty)$;

Функция не является ни четной, ни нечетной:
$y(-x) = 5(-x)^2 — 15(-x) — 4 = 5x^2 + 15x — 4$;

У функции отсутствуют асимптоты;

Производная функции:
$y'(x) = 5(x^2)’ + (-15x — 4)’ = 5 \cdot 2x — 15 = 10x — 15$;

Промежуток возрастания:
$10x — 15 \geq 0$;
$10x \geq 15$;
$x \geq 1{,}5$;
$x = 1{,}5$ — точка минимума;

$y_{\min} = 5 \cdot 1{,}5^2 — 15 \cdot 1{,}5 — 4 = 11{,}25 — 22{,}5 — 4 = -15{,}25$;

Функция возрастает на $[1{,}5; +\infty)$ и убывает на $(-\infty; 1{,}5]$;

Координаты некоторых точек:

График функции:

а) $y = 3x^2 — 4x + 5$

1) Область определения:

Это квадратичная функция, определена при всех $x \in \mathbb{R}$.
Ответ:
$D(y) = (-\infty; +\infty)$

2) Чётность/нечётность:

Проверим:

$$y(-x)=3(-x{)}^2-4(-x)+5=3x^2+4x+5\mathrm{\ne }y(x),$$

$$y(-x) = 3(-x)^2 — 4(-x) + 5 = 3x^2 + 4x + 5 \neq y(x), \quad \text{и} \quad \neq -y(x)$$

Вывод: функция не является ни чётной, ни нечётной.

3) Асимптоты:

Квадратичные функции не имеют вертикальных, горизонтальных или наклонных асимптот.
Ответ: Асимптоты отсутствуют.

4) Производная, экстремумы, интервалы монотонности:

Найдём первую производную:

$$y'(x) = \frac{d}{dx}(3x^2 — 4x + 5) = 6x — 4$$

Находим критические точки:

$$6x — 4 = 0 \quad \Rightarrow \quad x = \frac{2}{3}$$

Проверим знак производной:

• при $x < \frac{2}{3}$: $y'(x) < 0 \Rightarrow$ функция убывает;
• при $x > \frac{2}{3}$: $y'(x) > 0 \Rightarrow$ функция возрастает.

Значит, в точке $x = \frac{2}{3}$ — минимум.

Найдём значение функции в этой точке:

$$y\left(\frac{2}{3}\right) = 3\left(\frac{2}{3}\right)^2 — 4 \cdot \frac{2}{3} + 5 = \frac{12}{9} — \frac{8}{3} + 5 = \frac{4}{3} — \frac{8}{3} + \frac{15}{3} = \frac{11}{3}$$

Ответ:

• Точка минимума: $\left(\frac{2}{3}, \frac{11}{3}\right)$
• Убывает: $(-\infty; \frac{2}{3})$
• Возрастает: $(\frac{2}{3}; +\infty)$

5) Дополнительные точки:

Подставим значения:

6) График функции:

• Тип: парабола.
• Коэффициент при $x^2$ положительный → ветви вверх.
• Вершина:

$$x_0 = \frac{-b}{2a} = \frac{4}{6} = \frac{2}{3}, \quad y_0 = \frac{11}{3}$$

• Ось симметрии: $x = \frac{2}{3}$

Итоговое исследование функции:

$$y = 3x^2 — 4x + 5$$

• О.Д.: $(-\infty; +\infty)$
• Чётность: нечетная и нечетная
• Асимптоты: нет
• Производная: $y'(x) = 6x — 4$
• Экстремум: минимум в точке $\left(\frac{2}{3}, \frac{11}{3}\right)$
• Монотонность:
  • Убывает на $(-\infty; \frac{2}{3})$
  • Возрастает на $(\frac{2}{3}; +\infty)$
• График: парабола с вершиной в $\left(\frac{2}{3}, \frac{11}{3}\right)$, ветви вверх
• Дополнительные точки:
  • $(-1; 12), (0; 5), (1; 4), (2; 9)$

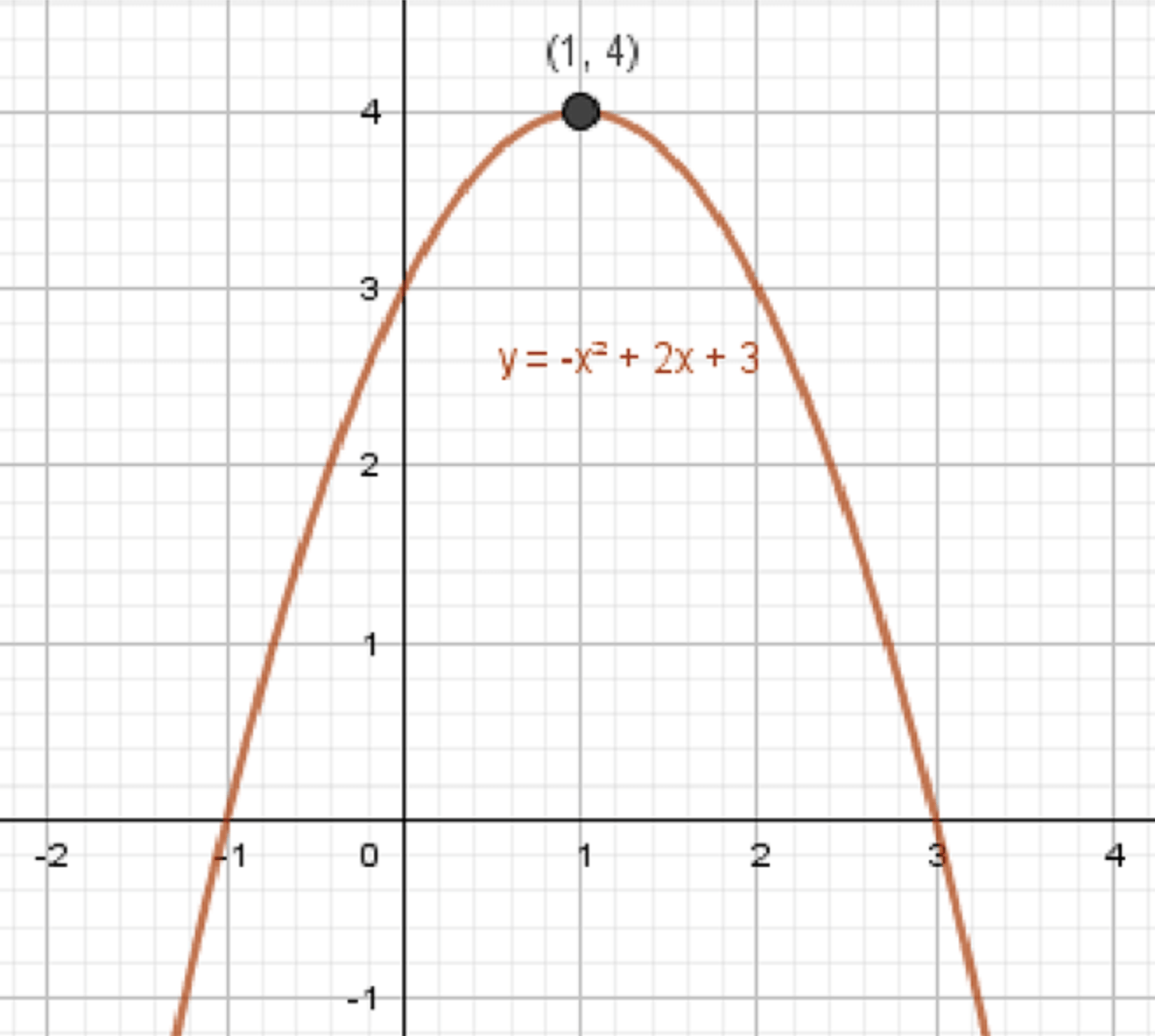
б) $y = 3 + 2x — x^2$

1) Область определения функции:

Функция определена при всех значениях $x \in \mathbb{R}$.
Ответ:

$$D(y) = (-\infty; +\infty)$$

2) Чётность/нечётность функции:

Проверим:

$$y(-x)=3+2(-x)-(-x{)}^2=3-2x-x^2\mathrm{\ne }y(x),$$

$$y(-x) = 3 + 2(-x) — (-x)^2 = 3 — 2x — x^2 \neq y(x), \quad \text{и} \quad \neq -y(x)$$

Вывод: Функция не является ни чётной, ни нечётной.

3) Асимптоты:

Функция — квадратичная, не имеет асимптот.
Ответ: Асимптоты отсутствуют.

4) Исследование производной, экстремумы, монотонность:

Найдём производную:

$$y'(x) = \frac{d}{dx}(3 + 2x — x^2) = 2 — 2x$$

Найдём критическую точку:

$$2 — 2x = 0 \quad \Rightarrow \quad x = 1$$

Анализ производной:

• при $x < 1$: $y'(x) > 0 \Rightarrow$ функция возрастает;
• при $x > 1$: $y'(x) < 0 \Rightarrow$ функция убывает;

Следовательно, точка максимума — $x = 1$

Найдём значение функции в этой точке:

$$y(1) = 3 + 2 \cdot 1 — 1^2 = 3 + 2 — 1 = 4$$

Вывод:

• Точка максимума: $(1, 4)$
• Возрастает: $(-\infty; 1)$
• Убывает: $(1; +\infty)$

5) Дополнительные точки:

Вычислим значения функции:

6) График функции:

• Тип графика: парабола.
• Ветви направлены вниз (коэффициент при $x^2$ отрицательный).
• Вершина:

$$x_0 = \frac{-b}{2a} = \frac{-2}{-2} = 1, \quad y_0 = 4$$

• Ось симметрии: $x = 1$

Итоговое исследование функции:

$$y = 3 + 2x — x^2$$

• Область определения: $(-\infty; +\infty)$
• Чётность: нечетная и нечетная
• Асимптоты: отсутствуют
• Производная: $y'(x) = 2 — 2x$
• Экстремум: максимум в точке $(1, 4)$
• Монотонность:
  • возрастает на $(-\infty; 1)$
  • убывает на $(1; +\infty)$
• График: парабола, ветви вниз, вершина в $(1, 4)$
• Дополнительные точки:
  $(-1; 0), (0; 3), (2; 3), (3; 0)$

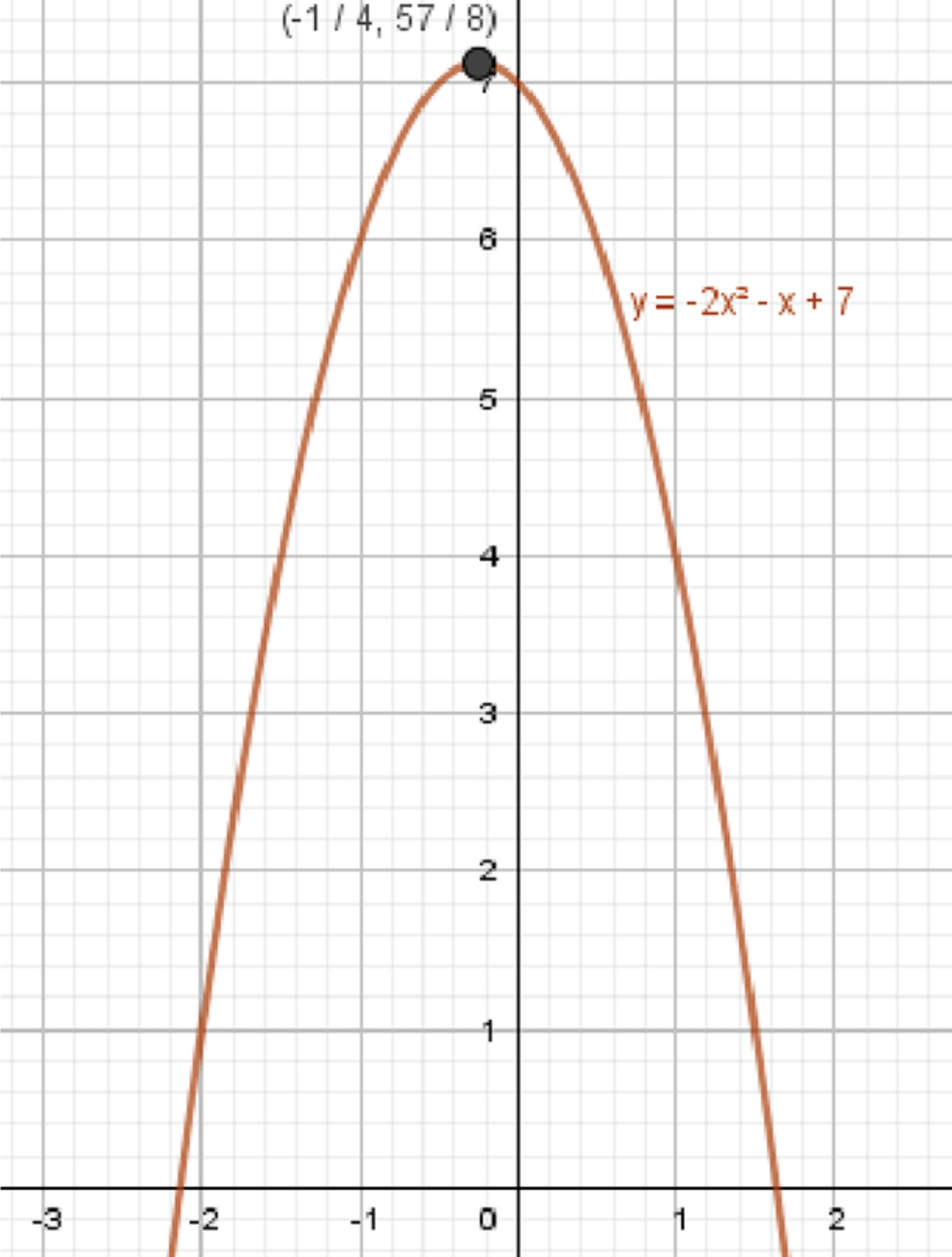
в) $y = 7 — x — 2x^2$

1) Область определения функции:

Функция — многочлен второй степени. Определена при всех $x \in \mathbb{R}$.
Ответ:

$$D(y) = (-\infty; +\infty)$$

2) Чётность/нечётность:

Проверим:

$$y(-x)=7-(-x)-2(-x{)}^2=7+x-2x^2\mathrm{\ne }y(x),$$

$$y(-x) = 7 — (-x) — 2(-x)^2 = 7 + x — 2x^2 \neq y(x), \quad \text{и} \quad \neq -y(x)$$

Вывод: Функция не является ни чётной, ни нечётной.

3) Асимптоты:

Поскольку функция квадратичная, асимптоты отсутствуют.

4) Исследование производной, экстремумы, монотонность:

Найдём первую производную:

$$y'(x) = \frac{d}{dx}(7 — x — 2x^2) = -1 — 4x$$

Найдём критическую точку:

$$-1 — 4x = 0 \quad \Rightarrow \quad x = -\frac{1}{4}$$

Исследуем знак производной:

• При $x < -\frac{1}{4}$: $y'(x) > 0 \Rightarrow$ функция возрастает;
• При $x > -\frac{1}{4}$: $y'(x) < 0 \Rightarrow$ функция убывает;

Следовательно, в точке $x = -\frac{1}{4}$ — максимум.

Найдём значение функции в этой точке:

$$y(-\frac{1}{4})=7-(-\frac{1}{4})-2\cdot {(-\frac{1}{4})}^2=7+\frac{1}{4}-2\cdot \frac{1}{16}=$$

$$y\left(-\frac{1}{4}\right) = 7 — \left(-\frac{1}{4}\right) — 2 \cdot \left(-\frac{1}{4}\right)^2 = 7 + \frac{1}{4} — 2 \cdot \frac{1}{16} = 7.25 — 0.125 = 7.125$$

Вывод:

• Максимум в точке $\left(-\frac{1}{4}, 7.125\right)$
• Возрастает на $(-\infty; -\frac{1}{4})$
• Убывает на $(-\frac{1}{4}; +\infty)$

5) Дополнительные точки:

Подставим значения в функцию:

6) График функции:

• График — парабола.
• Коэффициент при $x^2 = -2 < 0$ → ветви направлены вниз.
• Вершина:

  $$x_0 = \frac{-(-1)}{2 \cdot (-2)} = \frac{1}{-4} = -\frac{1}{4}, \quad y_0 = 7.125$$

• Ось симметрии: $x = -\frac{1}{4}$

Итоговое исследование функции:

$$y = 7 — x — 2x^2$$

• Область определения: $(-\infty; +\infty)$
• Чётность: ни чётная, ни нечётная
• Асимптоты: отсутствуют
• Производная: $y'(x) = -1 — 4x$
• Экстремум: максимум в точке $\left(-\frac{1}{4}, 7.125\right)$
• Монотонность:
  • возрастает на $(-\infty; -\frac{1}{4})$
  • убывает на $(-\frac{1}{4}; +\infty)$
• График: парабола, ветви вниз, вершина $\left(-\frac{1}{4}, 7.125\right)$
• Дополнительные точки:
  $(-2; 1), (-1; 6), (1; 4), (2; -3)$

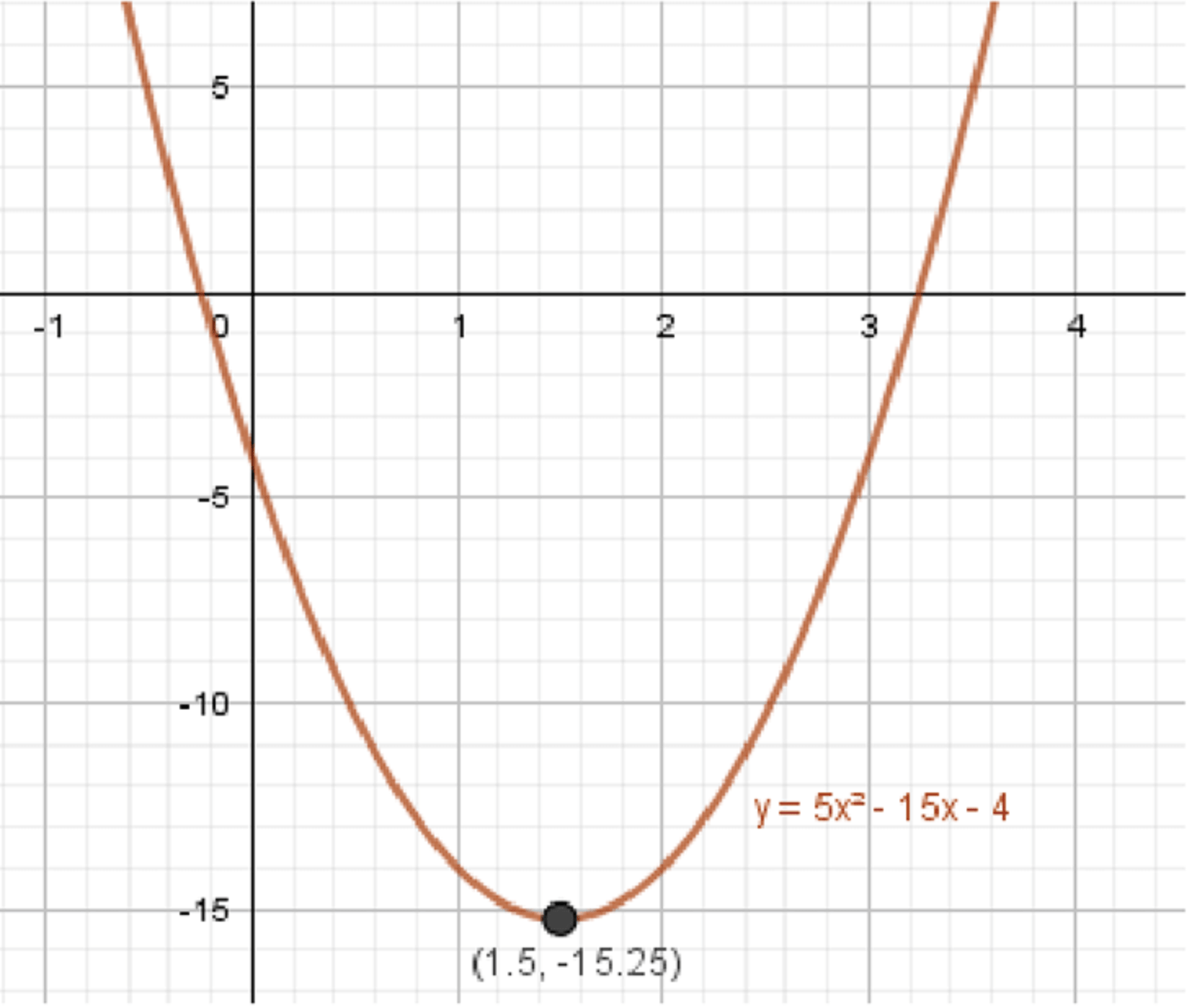
г) $y = 5x^2 — 15x — 4$

1) Область определения функции:

Это многочлен второй степени. Определён при всех $x \in \mathbb{R}$.
Ответ:

$$D(y) = (-\infty; +\infty)$$

2) Чётность/нечётность функции:

Проверим:

$$y(-x)=5(-x{)}^2-15(-x)-4=5x^2+15x-4\mathrm{\ne }y(x),$$

$$y(-x) = 5(-x)^2 — 15(-x) — 4 = 5x^2 + 15x — 4 \neq y(x), \quad \text{и} \quad \neq -y(x)$$

Вывод: Функция не является ни чётной, ни нечётной.

3) Асимптоты:

Функция квадратичная → асимптоты отсутствуют.

4) Производная, экстремумы, монотонность:

Найдём производную:

$$y'(x) = \frac{d}{dx}(5x^2 — 15x — 4) = 10x — 15$$

Найдём критическую точку:

$$10x — 15 = 0 \quad \Rightarrow \quad x = \frac{15}{10} = 1.5$$

Исследуем знак производной:

• $x < 1.5$: $y'(x) < 0 \Rightarrow$ функция убывает;
• $x > 1.5$: $y'(x) > 0 \Rightarrow$ функция возрастает;

Следовательно, в точке $x = 1.5$ — минимум.

Найдём значение функции в вершине:

$$y(1.5)=5\cdot (1.5{)}^2-15\cdot 1.5-4=5\cdot 2.25-22.5-4=$$

$$y(1.5) = 5 \cdot (1.5)^2 — 15 \cdot 1.5 — 4 = 5 \cdot 2.25 — 22.5 — 4 = 11.25 — 22.5 — 4 = -15.25$$

Вывод:

• Минимум: $(1.5, -15.25)$
• Убывает: $(-\infty; 1.5)$
• Возрастает: $(1.5; +\infty)$

5) Дополнительные точки:

Подставим значения:

Обратите внимание: значения симметричны относительно вершины $x = 1.5$

6) График функции:

• Тип графика: парабола
• Ветви направлены вверх (так как $a = 5 > 0$)
• Вершина:

  $$x_0 = \frac{-(-15)}{2 \cdot 5} = \frac{15}{10} = 1.5, \quad y_0 = -15.25$$

• Ось симметрии: $x = 1.5$

Итоговое исследование функции:

$$y = 5x^2 — 15x — 4$$

• Область определения: $(-\infty; +\infty)$
• Чётность: нечетная и нечетная
• Асимптоты: отсутствуют
• Производная: $y'(x) = 10x — 15$
• Экстремум: минимум в точке $(1.5, -15.25)$
• Монотонность:
  • убывает на $(-\infty; 1.5)$
  • возрастает на $(1.5; +\infty)$
• График: парабола, ветви вверх, вершина в точке $(1.5, -15.25)$
• Дополнительные точки:
  $(0;-4),(1;-14),(2;-14),(3;-4)$