ГДЗ 10-11 Класс Номер 31.4 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

а) $y = 3x^2 — x^3$

б) $y = -9x + x^3$

в) $y = x^3 + 3x^2$

г) $y=3x-x^3$

Исследовать функцию и построить ее график:

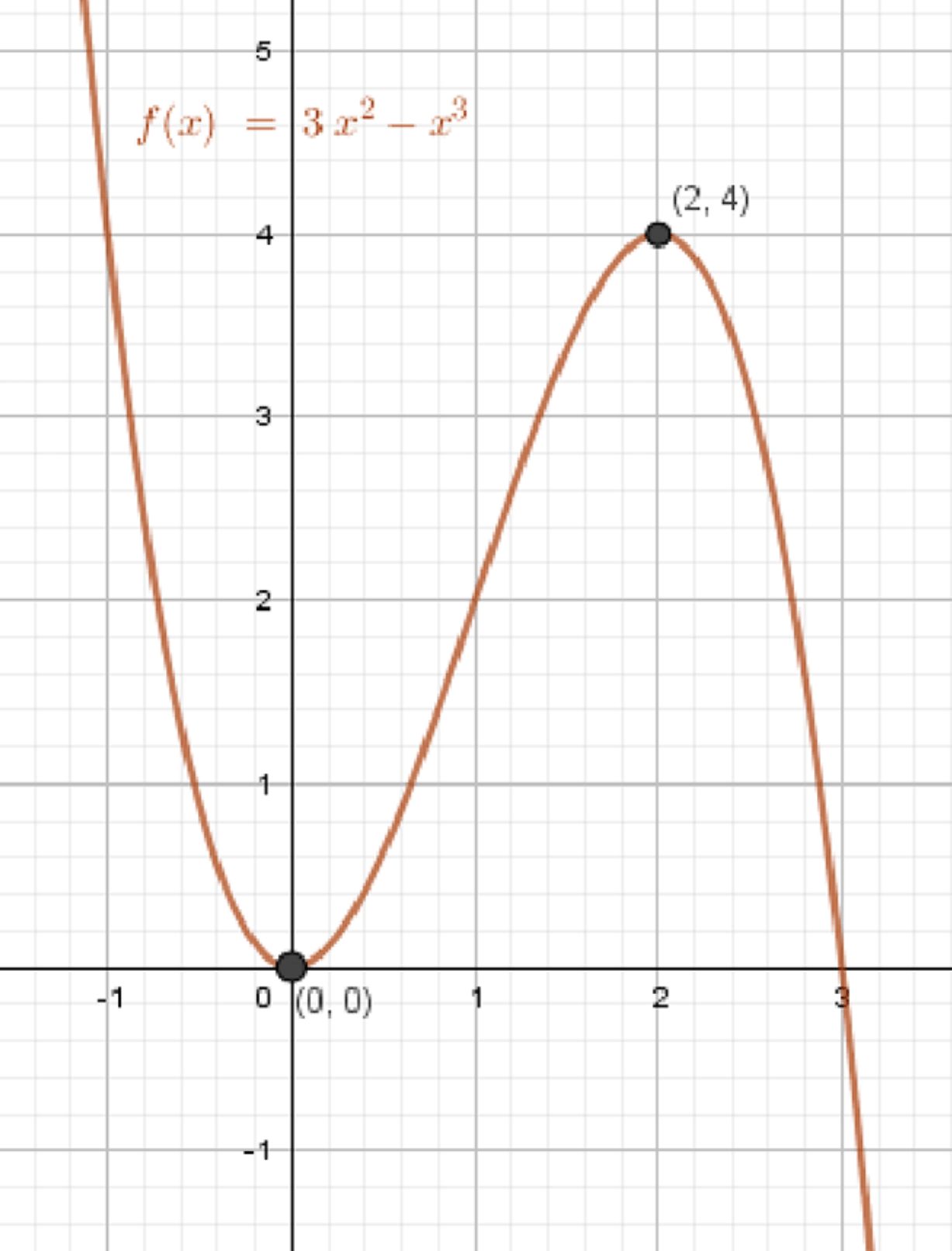
а) $y = 3x^2 — x^3$

Область определения функции:
$D(y) = (-\infty; +\infty)$;

Функция не является ни чётной, ни нечётной:

$$y(-x) = 3(-x)^2 — (-x)^3 = 3x^2 + x^3$$

У функции отсутствуют асимптоты;

Производная функции:

$$y'(x) = 3(x^2)’ — (x^3)’ = 6x — 3x^2$$

Промежуток возрастания:

$$6x — 3x^2 \geq 0 \Rightarrow 3x^2 — 6x \leq 0 \Rightarrow 3x(x — 2) \leq 0 \Rightarrow 0 \leq x \leq 2$$

$x = 0$ — точка минимума;
$x = 2$ — точка максимума;

$$y_{min} = 3 \cdot 0^2 — 0^3 = 0; \quad y_{max} = 3 \cdot 2^2 — 2^3 = 12 — 8 = 4$$

Функция возрастает на $[0; 2]$;
Функция убывает на $(-\infty; 0] \cup [2; +\infty)$;

Координаты некоторых точек:

График функции:

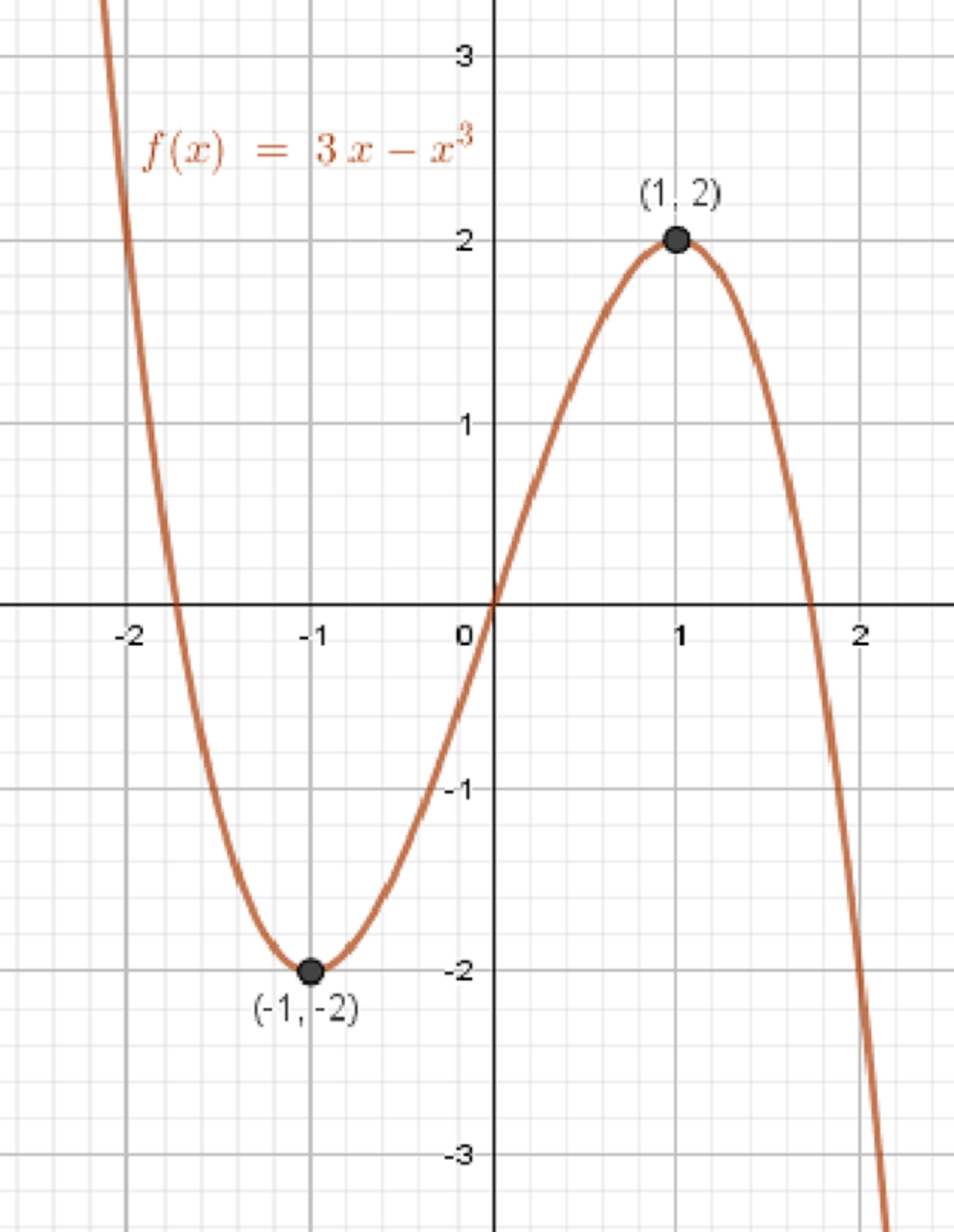
б) $y = -9x + x^3$

Область определения функции:
$D(y) = (-\infty; +\infty)$;

Функция является нечётной:

$$y(-x) = -9(-x) + (-x)^3 = 9x — x^3 = -y(x)$$

У функции отсутствуют асимптоты;

Производная функции:

$$y'(x) = (-9x)’ + (x^3)’ = -9 + 3x^2$$

Промежуток возрастания:

$$3x^2 — 9 \geq 0 \Rightarrow x^2 — 3 \geq 0 \Rightarrow (x + \sqrt{3})(x — \sqrt{3}) \geq 0$$ $$x \leq -\sqrt{3} \quad \text{или} \quad x \geq \sqrt{3}$$

$x = \sqrt{3}$ — точка минимума;
$x = -\sqrt{3}$ — точка максимума;

$$y_{min} = -9\sqrt{3} + (\sqrt{3})^3 = -6\sqrt{3}; \quad y_{max} = 9\sqrt{3} — 3\sqrt{3} = 6\sqrt{3}$$

Функция возрастает на $(-\infty; -\sqrt{3}] \cup [\sqrt{3}; +\infty)$;
Функция убывает на $[-\sqrt{3}; \sqrt{3}]$;

Координаты некоторых точек:

График функции:

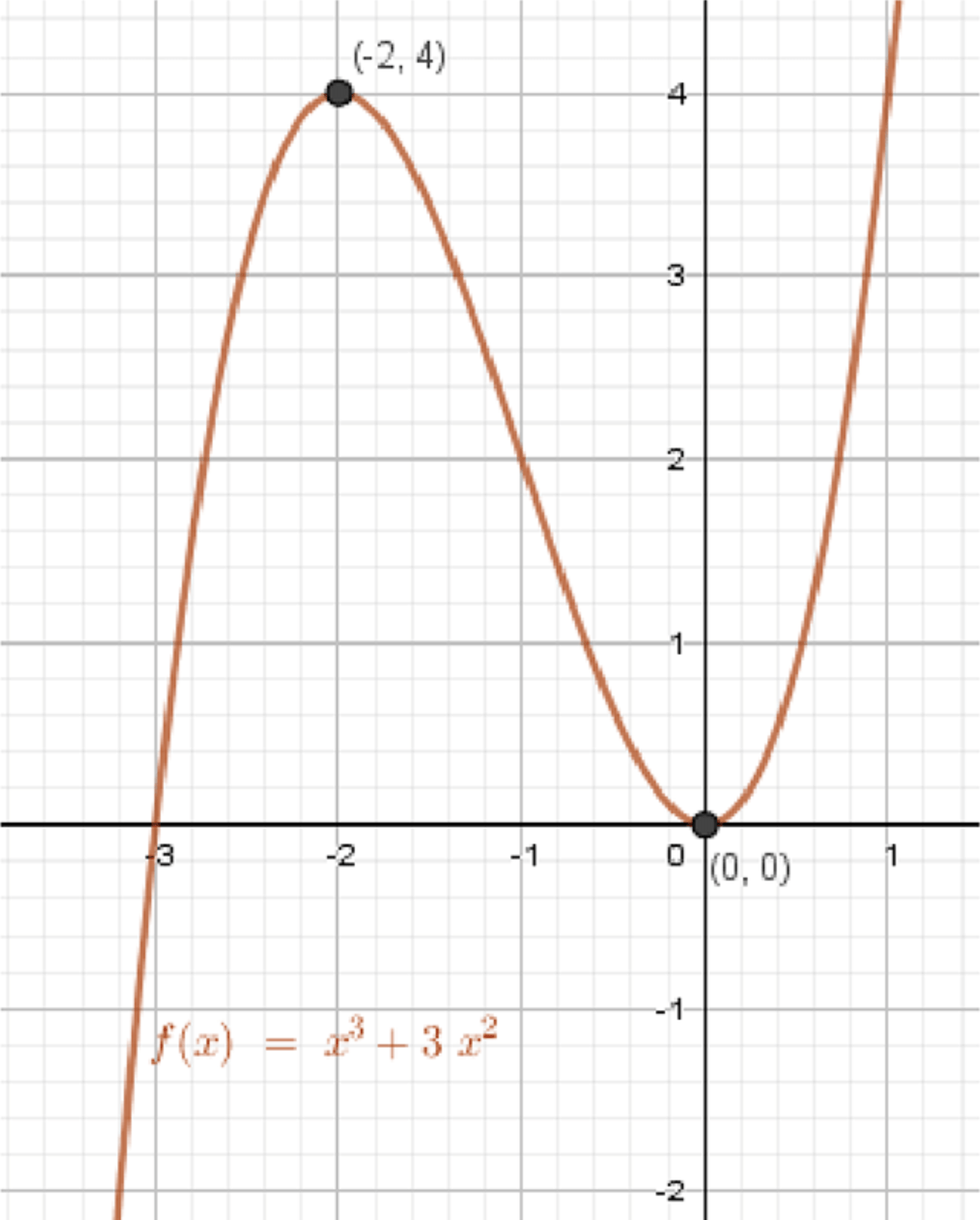
в) $y = x^3 + 3x^2$

Область определения функции:
$D(y) = (-\infty; +\infty)$;

Функция не является ни чётной, ни нечётной:

$$y(-x) = (-x)^3 + 3(-x)^2 = -x^3 + 3x^2$$

У функции отсутствуют асимптоты;

Производная функции:

$$y'(x) = (x^3)’ + 3(x^2)’ = 3x^2 + 6x$$

Промежуток возрастания:

$$3x^2 + 6x \geq 0 \Rightarrow 3x(x + 2) \geq 0 \Rightarrow x \leq -2 \quad \text{или} \quad x \geq 0$$

$x = 0$ — точка минимума;
$x = -2$ — точка максимума;

$$y_{min} = 0^3 + 3 \cdot 0^2 = 0; \quad y_{max} = (-2)^3 + 3 \cdot (-2)^2 = -8 + 12 = 4$$

Функция возрастает на $(-\infty; -2] \cup [0; +\infty)$;
Функция убывает на $[-2; 0]$;

Координаты некоторых точек:

График функции:

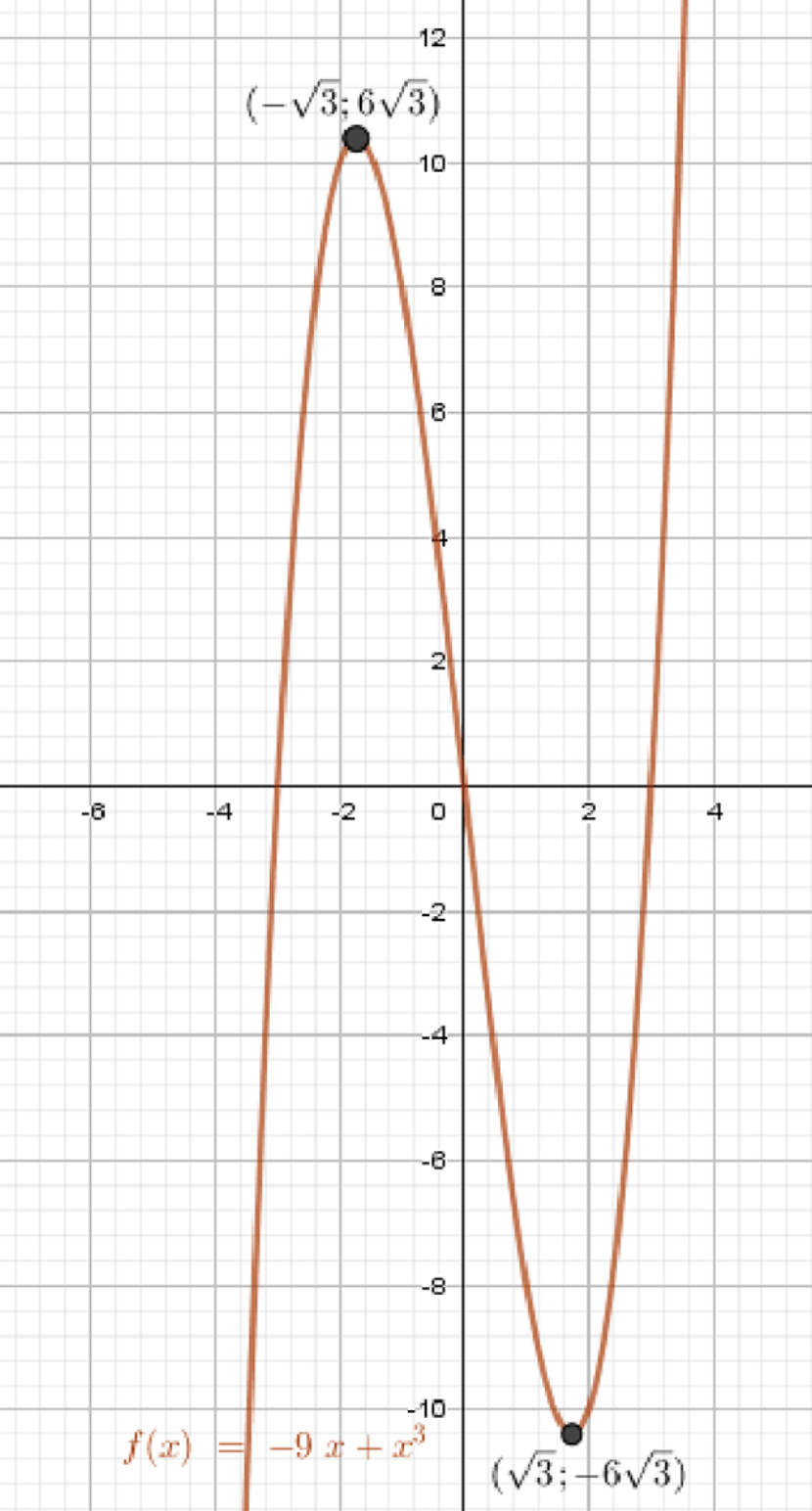
г) $y = 3x — x^3$

Область определения функции:
$D(y) = (-\infty; +\infty)$;

Функция является нечётной:

$$y(-x) = 3(-x) — (-x)^3 = -3x + x^3 = -y(x)$$

У функции отсутствуют асимптоты;

Производная функции:

$$y'(x) = (3x)’ — (x^3)’ = 3 — 3x^2$$

Промежуток возрастания:

$$3 — 3x^2 \geq 0 \Rightarrow 3x^2 — 3 \leq 0 \Rightarrow x^2 — 1 \leq 0 \Rightarrow -1 \leq x \leq 1$$

$x = -1$ — точка минимума;
$x = 1$ — точка максимума;

$$y_{min} = 3 \cdot (-1) — (-1)^3 = -3 + 1 = -2; \quad y_{max} = 3 \cdot 1 — 1^3 = 3 — 1 = 2$$

Функция возрастает на $[-1; 1]$;
Функция убывает на $(-\infty; -1] \cup [1; +\infty)$;

Координаты некоторых точек:

График функции:

а) $y = 3x^2 — x^3$

Шаг 1: Область определения

Функция состоит из многочлена, а многочлены определены на всей числовой прямой.
Ответ:

$$D(y) = (-\infty; +\infty)$$

Шаг 2: Чётность / нечётность функции

Проверим:

$$y(-x) = 3(-x)^2 — (-x)^3 = 3x^2 + x^3$$

Сравним с $y(x) = 3x^2 — x^3$:

• $y(-x) \ne y(x)$ → не чётная
• $y(-x) \ne -y(x)$ → не нечётная

Ответ:
Функция не является ни чётной, ни нечётной

Шаг 3: Асимптоты

Асимптоты бывают:

• Горизонтальные, если $\lim\limits_{x \to \infty} y = a$
• Вертикальные, если функция стремится к бесконечности в какой-то точке
• Наклонные, если $y \to kx + b$ при $x \to \infty$

Но:
$y = 3x^2 — x^3$ — многочлен.
У многочленов нет асимптот — функция уходит в бесконечность.

Ответ:
Асимптоты отсутствуют

Шаг 4: Находим производную

Находим первую производную:

$$y'(x) = (3x^2)’ — (x^3)’ = 6x — 3x^2$$

Найдём критические точки (где $y'(x) = 0$)

$$6x — 3x^2 = 0 \Rightarrow 3x(2 — x) = 0 \Rightarrow x = 0, \quad x = 2$$

Исследуем знак производной:

Разделим числовую прямую на интервалы:

• $(-\infty, 0)$
• $(0, 2)$
• $(2, +\infty)$

Проверим знак $y'(x) = 6x — 3x^2$ на каждом из них:

• На $(-\infty, 0)$:
  Подставим $x = -1$:
  $y'(-1) = -6 — 3 = -9 < 0$ → убывает
• На $(0, 2)$:
  Подставим $x = 1$:
  $y'(1) = 6 — 3 = 3 > 0$ → возрастает
• На $(2, \infty)$:
  Подставим $x = 3$:
  $y'(3) = 18 — 27 = -9 < 0$ → убывает

Выводы:

• $x = 0$ — точка минимума, потому что производная меняет знак с минуса на плюс.
• $x = 2$ — точка максимума, потому что производная меняет знак с плюса на минус.

Найдём значения функции в этих точках:

• $y(0) = 3 \cdot 0^2 — 0^3 = 0$
• $y(2) = 3 \cdot 4 — 8 = 12 — 8 = 4$

Ответ:

• Точка минимума: $(0; 0)$
• Точка максимума: $(2; 4)$
• Функция возрастает на $[0; 2]$, убывает на $(-\infty; 0] \cup [2; +\infty)$

Шаг 5: Точки для построения графика

Найдём значения в нескольких точках:

Эти точки полезны для построения эскиза.

Шаг 6: Построение графика (словесно)

• Точка минимума — $(0; 0)$, туда график «падает» слева и «вырастает» справа.
• Далее он доходит до максимума в $(2; 4)$, затем снова убывает.
• Кривая проходит через точки $(-1; 4)$, $(1; 2)$, $(3; 0)$
• График — кубическая кривая с одной вершиной «впадины» и одной «горки»

Финальный вид:
Плавная S-образная кривая, максимум в $(2; 4)$, минимум в $(0; 0)$, убывает на концах.

б) $y = -9x + x^3$

Шаг 1: Область определения

Функция состоит из суммы многочленов — линейного и кубического. Такие функции определены всюду.

Ответ:

$$D(y) = (-\infty; +\infty)$$

Шаг 2: Чётность / нечётность функции

Проверим:

$$y(-x) = -9(-x) + (-x)^3 = 9x — x^3 = -(-9x + x^3) = -y(x)$$

Вывод:

$$y(-x) = -y(x) \Rightarrow \text{функция является \textbf{нечётной}}$$

Шаг 3: Асимптоты

Функция — многочлен (степень 3), значит:

• не имеет вертикальных асимптот — нет точек разрыва
• не имеет горизонтальных — значение $y$ стремится к бесконечности
• не имеет наклонных — поведение на бесконечности задаётся самой функцией

Ответ:
У функции отсутствуют асимптоты

Шаг 4: Производная

Найдём первую производную:

$$y'(x) = (-9x)’ + (x^3)’ = -9 + 3x^2$$

Найдём критические точки:

Решим:

$$y'(x) = 0 \Rightarrow -9 + 3x^2 = 0 \Rightarrow x^2 = 3 \Rightarrow x = \pm\sqrt{3}$$

Это точки, где производная равна нулю — возможные экстремумы.

Определим интервалы возрастания и убывания:

Разделим ось $x$ на интервалы:

• $(-\infty; -\sqrt{3})$
• $(-\sqrt{3}; \sqrt{3})$
• $(\sqrt{3}; +\infty)$

Проверим знак производной:

• На $x < -\sqrt{3}$:
  Подставим $x = -2$:
  $y'(-2) = -9 + 3 \cdot 4 = -9 + 12 = 3 > 0$ → функция возрастает
• На $-\sqrt{3} < x < \sqrt{3}$:
  Подставим $x = 0$:
  $y'(0) = -9 < 0$ → убывает
• На $x > \sqrt{3}$:
  Подставим $x = 2$:
  $y'(2) = -9 + 3 \cdot 4 = 3 > 0$ → возрастает

Выводы:

• $x = -\sqrt{3}$ — максимум (смена производной с + на -)
• $x = \sqrt{3}$ — минимум (смена производной с — на +)

Найдём значения функции в этих точках:

$$y(\sqrt{3}) = -9\sqrt{3} + (\sqrt{3})^3 = -9\sqrt{3} + 3\sqrt{3} = -6\sqrt{3}$$ $$y(-\sqrt{3}) = -9(-\sqrt{3}) + (-\sqrt{3})^3 = 9\sqrt{3} — 3\sqrt{3} = 6\sqrt{3}$$

Ответ:

• Точка максимума: $x = -\sqrt{3}, \; y = 6\sqrt{3}$
• Точка минимума: $x = \sqrt{3}, \; y = -6\sqrt{3}$

Шаг 5: Промежутки монотонности

• Возрастание: $(-\infty; -\sqrt{3}] \cup [\sqrt{3}; +\infty)$
• Убывание: $[-\sqrt{3}; \sqrt{3}]$

Шаг 6: Точки для построения

Посчитаем значения:

Дополнительно можно взять:

• $x = -2$: $y = 18 — 8 = 10$
• $x = -3$: $y = 27 — 27 = 0$

Шаг 7: График функции (описание)

• Функция нечётная → график симметричен относительно начала координат
• Максимум в $(-\sqrt{3}; 6\sqrt{3})$, минимум в $(\sqrt{3}; -6\sqrt{3})$
• Проходит через $(0; 0)$, $(1; -8)$, $(3; 0)$
• Поведение:
  • слева — возрастает
  • затем — убывает (внутри интервала)
  • затем снова возрастает

Финальный вид:
Кривая, идущая вверх слева, достигает максимума, опускается, проходит через начало координат, достигает минимума, и снова уходит вверх. Форма напоминает «волнообразный» кубический график.

в) $y = x^3 + 3x^2$

Шаг 1: Область определения

Функция является многочленом. Многочлены определены при всех значениях $x$.

Ответ:

$$D(y) = (-\infty; +\infty)$$

Шаг 2: Чётность / нечётность функции

Проверим:

$$y(-x) = (-x)^3 + 3(-x)^2 = -x^3 + 3x^2$$

Сравним:

• $y(-x) \ne y(x)$ → не чётная
• $y(-x) \ne -y(x)$ → не нечётная

Вывод:
Функция не является ни чётной, ни нечётной

Шаг 3: Асимптоты

Функция — многочлен. Для многочленов:

• Горизонтальных асимптот нет
• Вертикальных нет (все значения допустимы)
• Наклонных — тоже нет (поведение на бесконечности описывается самой функцией)

Ответ:
Асимптоты отсутствуют

Шаг 4: Производная функции

$$y'(x) = (x^3)’ + 3(x^2)’ = 3x^2 + 6x$$

Найдём критические точки:

$$y'(x) = 0 \Rightarrow 3x^2 + 6x = 0 \Rightarrow 3x(x + 2) = 0 \Rightarrow x = 0, \quad x = -2$$

Знаки производной:

Разделим числовую прямую на интервалы:

• $(-\infty; -2)$
• $(-2; 0)$
• $(0; +\infty)$

Проверим знак $y'(x) = 3x(x + 2)$:

• На $(-\infty; -2)$:
  $x = -3 \Rightarrow y’ = 3(-3)(-1) = 9 > 0$ → возрастает
• На $(-2; 0)$:
  $x = -1 \Rightarrow y’ = 3(-1)(1) = -3 < 0$ → убывает
• На $(0; \infty)$:
  $x = 1 \Rightarrow y’ = 3(1)(3) = 9 > 0$ → возрастает

Типы точек:

• $x = -2$: производная меняется с $+ \to —$ → максимум
• $x = 0$: производная меняется с $— \to +$ → минимум

Значения функции в точках экстремума:

• $y(-2) = (-2)^3 + 3(-2)^2 = -8 + 12 = 4$
• $y(0) = 0 + 0 = 0$

Ответ:

• Максимум: $(-2; 4)$
• Минимум: $(0; 0)$

Шаг 5: Промежутки монотонности

• Функция возрастает на $(-\infty; -2] \cup [0; +\infty)$
• Функция убывает на $[-2; 0]$

Шаг 6: Точки для построения

Подставим значения:

Полезные точки: $(-3; 0)$, $(-2; 4)$, $(-1; 2)$, $(0; 0)$, $(1; 4)$

Шаг 7: Построение графика (словесно)

• Максимум в $(-2; 4)$
• Минимум в $(0; 0)$
• Функция сначала возрастает до $(-2; 4)$, затем убывает до $(0; 0)$, потом снова возрастает
• График проходит через:
  • $(-3; 0)$
  • $(-1; 2)$
  • $(0; 0)$
  • $(1; 4)$

Форма графика:

• Плавная волнообразная кривая
• Левая часть — подъём к максимуму
• Центральная — спуск к минимуму
• Правая часть — снова рост
• Похожа на «S», перевёрнутую влево

г) $y = 3x — x^3$

Шаг 1: Область определения

Функция — многочлен третьей степени (сумма одночленов $3x$ и $-x^3$). Такие функции определены на всей числовой прямой.

Ответ:

$$D(y) = (-\infty; +\infty)$$

Шаг 2: Чётность / нечётность функции

Проверим:

$$y(-x) = 3(-x) — (-x)^3 = -3x + x^3 = — (3x — x^3) = -y(x)$$

Вывод:

$$y(-x) = -y(x) \Rightarrow \text{функция \textbf{нечётная}}$$

Шаг 3: Асимптоты

Функция — многочлен. Многочлены не имеют:

• вертикальных асимптот (все точки определены)
• горизонтальных асимптот (на бесконечности $y \to \pm\infty$)
• наклонных асимптот (график не приближается к прямой — он сам уходит в бесконечность)

Ответ:
Асимптоты отсутствуют

Шаг 4: Первая производная

Найдём производную:

$$y'(x) = (3x)’ — (x^3)’ = 3 — 3x^2$$

Найдём критические точки (где $y'(x) = 0$):

$$3 — 3x^2 = 0 \Rightarrow x^2 = 1 \Rightarrow x = \pm 1$$

Разобьём числовую прямую и определим знак производной:

Интервалы:

• $(-\infty; -1)$
• $(-1; 1)$
• $(1; +\infty)$

Подставим в производную $y'(x) = 3 — 3x^2$:

• На $x < -1$:
  Подставим $x = -2$:
  $y'(-2) = 3 — 12 = -9 < 0$ → убывает
• На $x \in (-1; 1)$:
  Подставим $x = 0$:
  $y'(0) = 3 > 0$ → возрастает
• На $x > 1$:
  Подставим $x = 2$:
  $y'(2) = 3 — 12 = -9 < 0$ → убывает

Характер критических точек:

• $x = -1$: $y'(x)$ меняется с минуса на плюс → минимум
• $x = 1$: $y'(x)$ меняется с плюса на минус → максимум

Найдём значения функции в этих точках:

• $y(-1) = 3(-1) — (-1)^3 = -3 + 1 = -2$
• $y(1) = 3(1) — (1)^3 = 3 — 1 = 2$

Ответ:

• Минимум: $(-1; -2)$
• Максимум: $(1; 2)$

Шаг 5: Промежутки монотонности

• Функция убывает на $(-\infty; -1] \cup [1; +\infty)$
• Функция возрастает на $[-1; 1]$

Шаг 6: Точки для построения графика

Подставим значения в функцию:

Немного упрощённо:

• $y(-2) = -6 + 8 = 2$
• $y(-1) = -2$
• $y(0) = 0$
• $y(1) = 2$
• $y(2) = -2$
• $y(3) = -18$

Эти точки показывают симметрию: функция нечётная → график симметричен относительно начала координат.

Шаг 7: Построение графика (описание)

• Минимум: $(-1; -2)$
• Максимум: $(1; 2)$
• Проходит через:
  • $(-2; 2)$
  • $(-1; -2)$
  • $(0; 0)$
  • $(1; 2)$
  • $(2; -2)$
  • $(3; -18)$

Форма графика:

• График кубический, волнообразный
• Идёт вниз слева, до минимума $(-1; -2)$
• Затем резко вверх к максимуму $(1; 2)$
• Потом снова уходит вниз
• Нечётность отражается в симметрии: точки $(x; y)$ и $(-x; -y)$ отражаются друг в друге относительно начала координат