ГДЗ 10-11 Класс Номер 31.7 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы Задача
Постройте график функции:
а) y = − x 4 + 5 x 2 − 4 y = -x^4 + 5x^2 — 4
б) y = x 5 − 5 x y = x^5 — 5x
в) y = 2 x 4 − 9 x 2 + 7 y = 2x^4 — 9x^2 + 7
г) y = 5 x 3 − 3 x 5 y = 5x^3 — 3x^5
Краткий ответ:
Построить график функции:
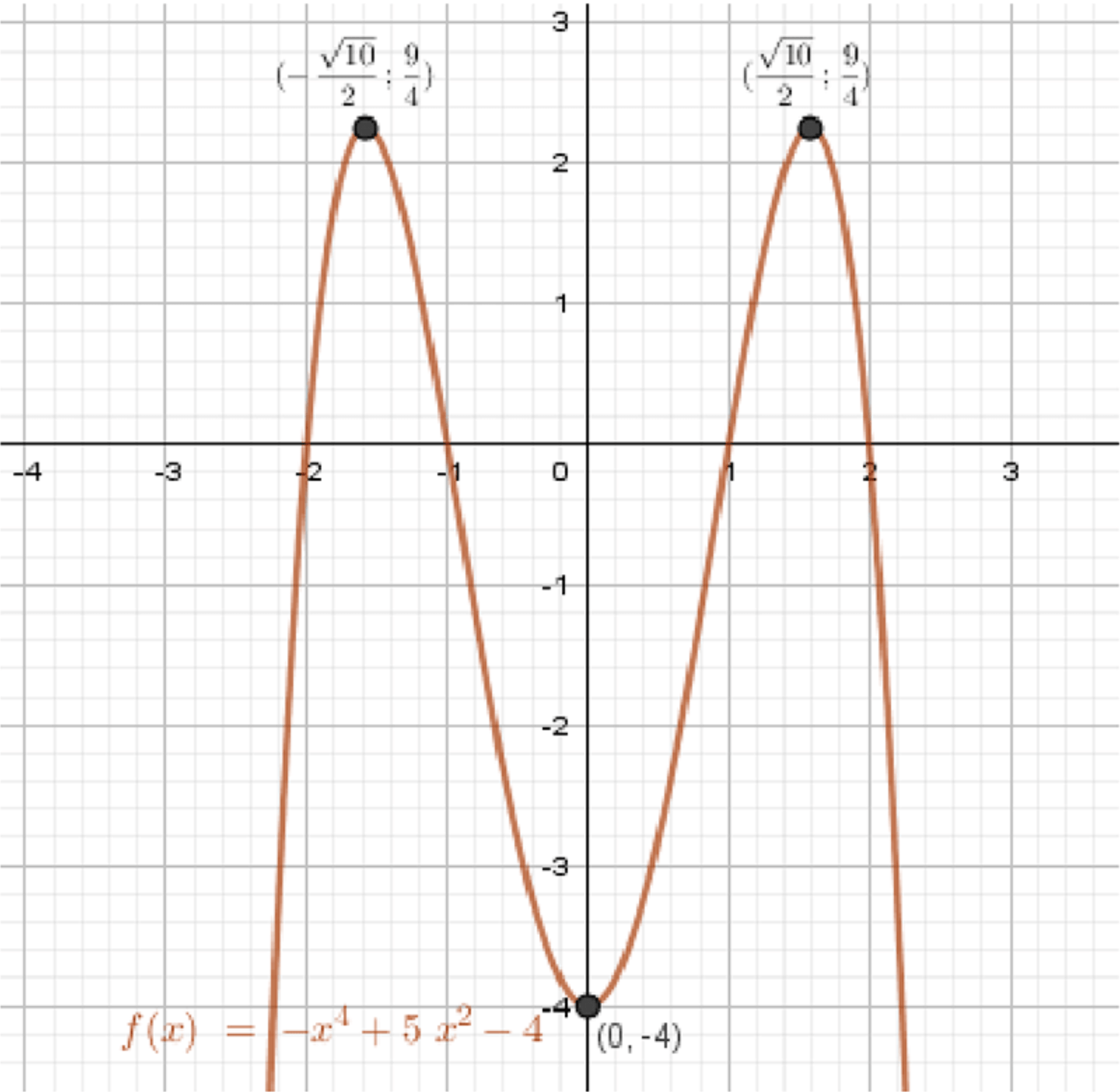
а) y = − x 4 + 5 x 2 − 4 y = -x^4 + 5x^2 — 4
Область определения функции:D ( y ) = ( − ∞ ; + ∞ ) D(y) = (-\infty; +\infty)
Функция является четной:y ( − x ) = − ( − x ) 4 + 5 ( − x ) 2 − 4 = − x 4 + 5 x 2 − 4 = y ( x ) y(-x) = -(-x)^4 + 5(-x)^2 — 4 = -x^4 + 5x^2 — 4 = y(x)
Производная функции:y ′ ( x ) = − ( x 4 ) ′ + 5 ( x 2 ) ′ − ( 4 ) ′ y'(x) = -(x^4)’ + 5(x^2)’ — (4)’ y ′ ( x ) = − 4 x 3 + 5 ⋅ 2 x − 0 = 10 x − 4 x 3 y'(x) = -4x^3 + 5 \cdot 2x — 0 = 10x — 4x^3
Промежуток возрастания:10 x − 4 x 3 ≥ 0 10x — 4x^3 \geq 0 4 x 3 − 10 x ≤ 0 4x^3 — 10x \leq 0 2 x ( 2 x 2 − 5 ) ≤ 0 2x(2x^2 — 5) \leq 0 ( 2 x + 5 ) ( 2 x − 5 ) ≤ 0 (\sqrt{2}x + \sqrt{5})(\sqrt{2}x — \sqrt{5}) \leq 0 x ≤ − 2 , 5 x \leq -\sqrt{2,5} 0 ≤ x ≤ 2 , 5 0 \leq x \leq \sqrt{2,5} x = 0 x = 0 x = ± 2 , 5 x = \pm \sqrt{2,5} y m i n = − 0 4 + 5 ⋅ 0 2 − 4 = − 4 y_{min} = -0^4 + 5 \cdot 0^2 — 4 = -4 y m a x = − ( ± 2 , 5 ) 4 + 5 ( ± 2 , 5 ) 2 − 4 = − 6 , 25 + 12 , 5 − 4 = 2 , 25 y_{max} = -(\pm \sqrt{2,5})^4 + 5(\pm \sqrt{2,5})^2 — 4 = -6,25 + 12,5 — 4 = 2,25
Координаты некоторых точек:
График функции:
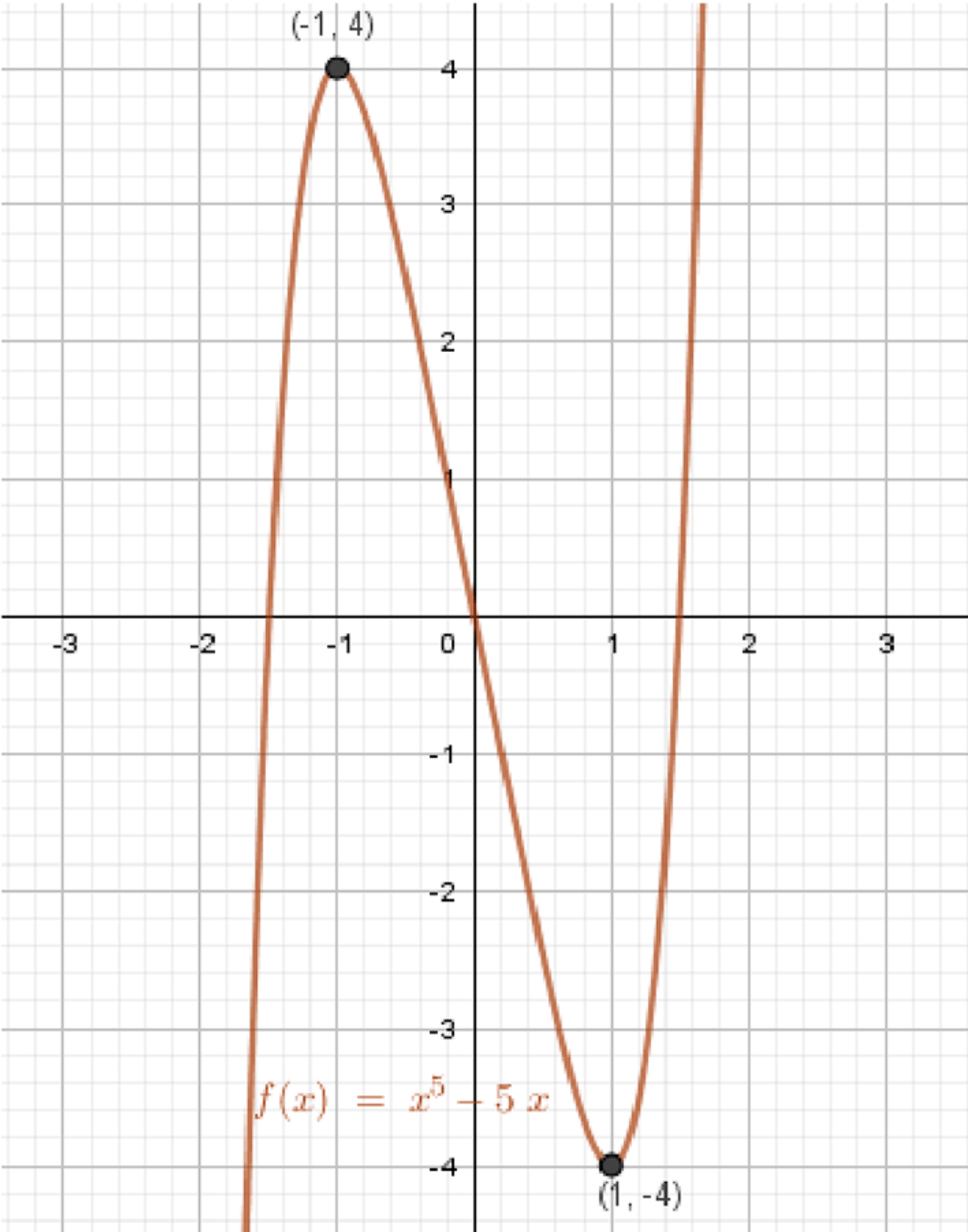
б) y = x 5 − 5 x y = x^5 — 5x
Область определения функции:D ( y ) = ( − ∞ ; + ∞ ) D(y) = (-\infty; +\infty)
Функция является нечетной:y ( − x ) = ( − x ) 5 − 5 ( − x ) = − x 5 + 5 x = − y ( x ) y(-x) = (-x)^5 — 5(-x) = -x^5 + 5x = -y(x)
Производная функции:y ′ ( x ) = ( x 5 ) ′ − ( 5 x ) ′ = 5 x 4 − 5 y'(x) = (x^5)’ — (5x)’ = 5x^4 — 5
Промежуток возрастания:5 x 4 − 5 ≥ 0 5x^4 — 5 \geq 0 ( x 2 − 1 ) ≥ 0 (x^2 — 1) \geq 0 ( x + 1 ) ( x − 1 ) ≥ 0 (x + 1)(x — 1) \geq 0 x ≤ − 1 x \leq -1 x ≥ 1 x \geq 1 x = 1 x = 1 x = − 1 x = -1 y m i n = 1 5 − 5 ⋅ 1 = 1 − 5 = − 4 y_{min} = 1^5 — 5 \cdot 1 = 1 — 5 = -4 y m a x = ( − 1 ) 5 − 5 ⋅ ( − 1 ) = − 1 + 5 = 4 y_{max} = (-1)^5 — 5 \cdot (-1) = -1 + 5 = 4
Координаты некоторых точек:
График функции:
в) y = 2 x 4 − 9 x 2 + 7 y = 2x^4 — 9x^2 + 7
Область определения функции:D ( y ) = ( − ∞ ; + ∞ ) D(y) = (-\infty; +\infty)
Функция является четной:y ( − x ) = 2 ( − x ) 4 − 9 ( − x ) 2 + 7 = 2 x 4 − 9 x 2 + 7 y(-x) = 2(-x)^4 — 9(-x)^2 + 7 = 2x^4 — 9x^2 + 7
Производная функции:y ′ ( x ) = 2 ( x 4 ) ′ − 9 ( x 2 ) ′ + ( 7 ) ′ y'(x) = 2(x^4)’ — 9(x^2)’ + (7)’ y ′ ( x ) = 2 ⋅ 4 x 3 − 9 ⋅ 2 x + 0 = 8 x 3 − 18 x y'(x) = 2 \cdot 4x^3 — 9 \cdot 2x + 0 = 8x^3 — 18x
Промежуток возрастания:8 x 3 − 18 x ≥ 0 8x^3 — 18x \geq 0 2 x ( 4 x 2 − 9 ) ≥ 0 2x(4x^2 — 9) \geq 0 ( 2 x + 3 ) x ( 2 x − 3 ) ≥ 0 (2x + 3)x(2x — 3) \geq 0 − 1 , 5 ≤ x ≤ 0 -1,5 \leq x \leq 0 x ≥ 1 , 5 x \geq 1,5 x = ± 1 , 5 x = \pm 1,5 x = 0 x = 0 y m i n = 2 ( ± 1 , 5 ) 4 − 9 ( ± 1 , 5 ) 2 + 7 = 10 , 125 − 20 , 25 + 7 = − 3 , 125 y_{min} = 2(\pm 1,5)^4 — 9(\pm 1,5)^2 + 7 = 10,125 — 20,25 + 7 = -3,125 y m a x = 2 ⋅ 0 4 − 9 ⋅ 0 2 + 7 = 7 y_{max} = 2 \cdot 0^4 — 9 \cdot 0^2 + 7 = 7
Координаты некоторых точек:
График функции:
г) y = 5 x 3 − 3 x 5 y = 5x^3 — 3x^5
Область определения функции:D ( y ) = ( − ∞ ; + ∞ ) D(y) = (-\infty; +\infty)
Функция является нечетной:y ( − x ) = 5 ( − x ) 3 − 3 ( − x ) 5 = − 5 x 3 + 3 x 5 = − y ( x ) y(-x) = 5(-x)^3 — 3(-x)^5 = -5x^3 + 3x^5 = -y(x)
Производная функции:y ′ ( x ) = − 5 ( x 3 ) ′ + 3 ( x 5 ) ′ y'(x) = -5(x^3)’ + 3(x^5)’ y ′ ( x ) = − 5 ⋅ 3 x 2 + 3 ⋅ 5 x 4 = 15 x 4 − 15 x 2 y'(x) = -5 \cdot 3x^2 + 3 \cdot 5x^4 = 15x^4 — 15x^2
Промежуток возрастания:15 x 4 − 15 x 2 ≥ 0 15x^4 — 15x^2 \geq 0 15 x 2 ⋅ ( x 2 − 1 ) ≥ 0 15x^2 \cdot (x^2 — 1) \geq 0 ( x + 1 ) ( x − 1 ) ≥ 0 (x + 1)(x — 1) \geq 0 x ≤ − 1 x \leq -1 x ≥ 1 x \geq 1 x = 0 x = 0 x = 1 x = 1 x = − 1 x = -1 y m i n = 5 ⋅ 1 3 − 3 ⋅ 1 5 = 5 − 3 = 2 y_{min} = 5 \cdot 1^3 — 3 \cdot 1^5 = 5 — 3 = 2 y m a x = 5 ⋅ ( − 1 ) 3 − 3 ⋅ ( − 1 ) 5 = − 5 + 3 = − 2 y_{max} = 5 \cdot (-1)^3 — 3 \cdot (-1)^5 = -5 + 3 = -2
Координаты некоторых точек:
График функции:
Подробный ответ:
а) Функция:
y = − x 4 + 5 x 2 − 4 y = -x^4 + 5x^2 — 4
Шаг 1. Область определения
Функция является многочленом четвёртой степени.x ∈ R x \in \mathbb{R} Ответ:
D ( y ) = ( − ∞ ; + ∞ ) D(y) = (-\infty; +\infty)
Шаг 2. Чётность функции
Проверим значение функции при − x -x
y ( − x ) = − ( − x ) 4 + 5 ( − x ) 2 − 4 = − x 4 + 5 x 2 − 4 = y ( x ) y(-x) = -(-x)^4 + 5(-x)^2 — 4 = -x^4 + 5x^2 — 4 = y(x)
Вывод: функция чётная .симметричен относительно оси O y Oy .
Шаг 3. Производная
Найдём первую производную:
y ( x ) = − x 4 + 5 x 2 − 4 ⇒ y ′ ( x ) = − 4 x 3 + 10 x = 10 x − 4 x 3 y(x) = -x^4 + 5x^2 — 4 \Rightarrow y'(x) = -4x^3 + 10x = 10x — 4x^3
Шаг 4. Экстремумы и промежутки монотонности
Решим неравенство:
y ′ ( x ) = 10 x − 4 x 3 ≥ 0 ⇒ 4 x 3 − 10 x ≤ 0 ⇒ 2 x ( 2 x 2 − 5 ) ≤ 0 y'(x) = 10x — 4x^3 \geq 0 \Rightarrow 4x^3 — 10x \leq 0 \Rightarrow 2x(2x^2 — 5) \leq 0
Решим неравенство:
2 x ( 2 x 2 − 5 ) ≤ 0 2x(2x^2 — 5) \leq 0 Корни:
x = 0 x = 0 2 x 2 − 5 = 0 ⇒ x = ± 2.5 2x^2 — 5 = 0 \Rightarrow x = \pm \sqrt{2.5} Промежутки:
На ( − ∞ ; − 2.5 ) (-\infty; -\sqrt{2.5}) На [ − 2.5 ; 0 ] [-\sqrt{2.5}; 0] На [ 0 ; 2.5 ] [0; \sqrt{2.5}] На ( 2.5 ; + ∞ ) (\sqrt{2.5}; +\infty) Вывод:
Функция имеет локальный минимум в x = 0 x = 0 Локальные максимумы в точках x = − 2.5 x = -\sqrt{2.5} x = 2.5 x = \sqrt{2.5} Шаг 5. Значения функции в точках экстремума
Минимум:
y ( 0 ) = − 0 4 + 5 ⋅ 0 2 − 4 = − 4 y(0) = -0^4 + 5 \cdot 0^2 — 4 = -4
Максимум:
Пусть x = 2.5 x = \sqrt{2.5}
x 2 = 2.5 x^2 = 2.5 x 4 = ( x 2 ) 2 = 6.25 x^4 = (x^2)^2 = 6.25 y = − 6.25 + 12.5 − 4 = 2.25 y = -6.25 + 12.5 — 4 = 2.25
Аналогично для x = − 2.5 x = -\sqrt{2.5}
Шаг 6. Таблица значений функции
x x y y 1 − 1 + 5 − 4 = 0 -1 + 5 — 4 = 0 2 − 16 + 20 − 4 = 0 -16 + 20 — 4 = 0 3 − 81 + 45 − 4 = − 40 -81 + 45 — 4 = -40
Шаг 7. Описание графика
График симметричен относительно оси y y Максимумы по бокам от оси y y x = ± 2.5 x = \pm \sqrt{2.5} Минимум в точке x = 0 x = 0 y = − 4 y = -4 Форма графика напоминает «двугорбую» параболу, прижатую вниз: убывает, растёт, затем снова убывает.
б) Функция:
y = x 5 − 5 x y = x^5 — 5x
Шаг 1. Область определения
Многочлен пятой степени — определён при всех x x
D ( y ) = ( − ∞ ; + ∞ ) D(y) = (-\infty; +\infty)
Шаг 2. Нечётность функции
y ( − x ) = ( − x ) 5 − 5 ( − x ) = − x 5 + 5 x = − ( x 5 − 5 x ) = − y ( x ) y(-x) = (-x)^5 — 5(-x) = -x^5 + 5x = — (x^5 — 5x) = -y(x)
Вывод: функция нечётная
Шаг 3. Производная
y ′ ( x ) = 5 x 4 − 5 y'(x) = 5x^4 — 5
Решим неравенство:
5 x 4 − 5 ≥ 0 ⇒ x 4 ≥ 1 ⇒ ∣ x ∣ ≥ 1 5x^4 — 5 \geq 0 \Rightarrow x^4 \geq 1 \Rightarrow |x| \geq 1
Промежутки:
Убывает на ( − 1 ; 1 ) (-1; 1) Возрастает на ( − ∞ ; − 1 ] ∪ [ 1 ; + ∞ ) (-\infty; -1] \cup [1; +\infty) Шаг 4. Экстремумы
При x = 1 x = 1
y = 1 − 5 = − 4 ⇒ локальный минимум y = 1 — 5 = -4 \Rightarrow \text{локальный минимум}
При x = − 1 x = -1
y = − 1 + 5 = 4 ⇒ локальный максимум y = -1 + 5 = 4 \Rightarrow \text{локальный максимум}
Шаг 5. Таблица значений
x x y y 0 0 2 32 − 10 = 22 32 — 10 = 22
Шаг 6. Описание графика
График нечётный , симметричен относительно начала координат. Имеет максимум в точке x = − 1 x = -1 y = 4 y = 4 Минимум в точке x = 1 x = 1 y = − 4 y = -4 График напоминает продолговатую S-образную кривую, пересекающую ось x x x = 0 x = 0 x = 5 x = \sqrt{5} x = − 5 x = -\sqrt{5}
в) Функция:
y = 2 x 4 − 9 x 2 + 7 y = 2x^4 — 9x^2 + 7
Шаг 1. Область определения
Функция — многочлен ⇒ определена на всей числовой прямой.
D ( y ) = ( − ∞ ; + ∞ ) D(y) = (-\infty; +\infty)
Шаг 2. Чётность
y ( − x ) = 2 x 4 − 9 x 2 + 7 = y ( x ) ⇒ функция чётная y(-x) = 2x^4 — 9x^2 + 7 = y(x) \Rightarrow \text{функция чётная}
Шаг 3. Производная
y ′ ( x ) = 8 x 3 − 18 x = 2 x ( 4 x 2 − 9 ) y'(x) = 8x^3 — 18x = 2x(4x^2 — 9)
Решим:
2 x ( 4 x 2 − 9 ) ≥ 0 ⇒ ( 2 x + 3 ) ( 2 x − 3 ) x ≥ 0 2x(4x^2 — 9) \geq 0 \Rightarrow (2x + 3)(2x — 3)x \geq 0
Корни:
x = 0 x = 0 x = ± 1.5 x = \pm 1.5 Промежутки:
Возрастает: [ − 1.5 ; 0 ] ∪ [ 1.5 ; + ∞ ) [-1.5; 0] \cup [1.5; +\infty) Убывает: ( − ∞ ; − 1.5 ] ∪ [ 0 ; 1.5 ] (-\infty; -1.5] \cup [0; 1.5] Шаг 4. Экстремумы
Максимум в x = 0 x = 0
y = 2 ⋅ 0 4 − 9 ⋅ 0 2 + 7 = 7 y = 2 \cdot 0^4 — 9 \cdot 0^2 + 7 = 7
Минимум в x = ± 1.5 x = \pm 1.5
x 2 = 2.25 x^2 = 2.25 x 4 = 5.0625 x^4 = 5.0625 y = 2 ⋅ 5.0625 − 9 ⋅ 2.25 + 7 = 10.125 − 20.25 + 7 = − 3.125 y = 2 \cdot 5.0625 — 9 \cdot 2.25 + 7 = 10.125 — 20.25 + 7 = -3.125 Шаг 5. Таблица значений
x x y y 1 2 − 9 + 7 = 0 2 — 9 + 7 = 0 2 32 − 36 + 7 = 3 32 — 36 + 7 = 3 3 162 − 81 + 7 = 88 162 — 81 + 7 = 88
Шаг 6. Описание графика
График чётный, симметричен относительно оси O y Oy Имеет максимум в центре (x = 0 x = 0 y = 7 y = 7 Имеет две симметричные точки минимума при x = ± 1.5 x = \pm 1.5 y = − 3.125 y = -3.125 График напоминает двугорбую параболу , но с максимумом в середине и минимумами по бокам
г) Функция:
y = 5 x 3 − 3 x 5 y = 5x^3 — 3x^5
Шаг 1. Область определения
Многочлен ⇒ определён всюду:
D ( y ) = ( − ∞ ; + ∞ ) D(y) = (-\infty; +\infty)
Шаг 2. Нечётность
y ( − x ) = − 5 x 3 + 3 x 5 = − y ( x ) ⇒ функция нечётная y(-x) = -5x^3 + 3x^5 = -y(x) \Rightarrow \text{функция нечётная}
Шаг 3. Производная
y ′ ( x ) = 15 x 2 − 15 x 4 = 15 x 2 ( 1 − x 2 ) y'(x) = 15x^2 — 15x^4 = 15x^2(1 — x^2)
Промежутки:
Производная ≥ 0 \geq 0 ∣ x ∣ ≤ 1 |x| \leq 1 Производная < 0 < 0 ∣ x ∣ > 1 |x| > 1 Функция возрастает: [ − 1 ; 1 ] [-1; 1] ( − ∞ ; − 1 ] ∪ [ 1 ; + ∞ ) (-\infty; -1] \cup [1; +\infty)
Шаг 4. Экстремумы
Максимум в x = − 1 x = -1
y = − 5 + 3 = − 2 y = -5 + 3 = -2
Минимум в x = 1 x = 1
y = 5 − 3 = 2 y = 5 — 3 = 2
Шаг 5. Таблица значений
x x y y 0 0 2 40 − 96 = − 56 40 — 96 = -56
Шаг 6. Описание графика
Нечётная функция, симметрична относительно начала координат Имеет максимум в x = − 1 x = -1 x = 1 x = 1 Функция убывает на концах, растёт в центральной части Форма графика — плавная кривая с тремя перегибами , напоминающая «S» перевёрнутую по вертикали