ГДЗ 10-11 Класс Номер 31.8 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

а) $y = (x — 1)^2 \cdot (x + 2)$;

б) $y = \frac{256}{9}x(x — 1)^3$;

в) $y = (x + 2)^2 \cdot (x — 3)$;

г) $y = x^3 \cdot (2 — x)$

Построить график функции:

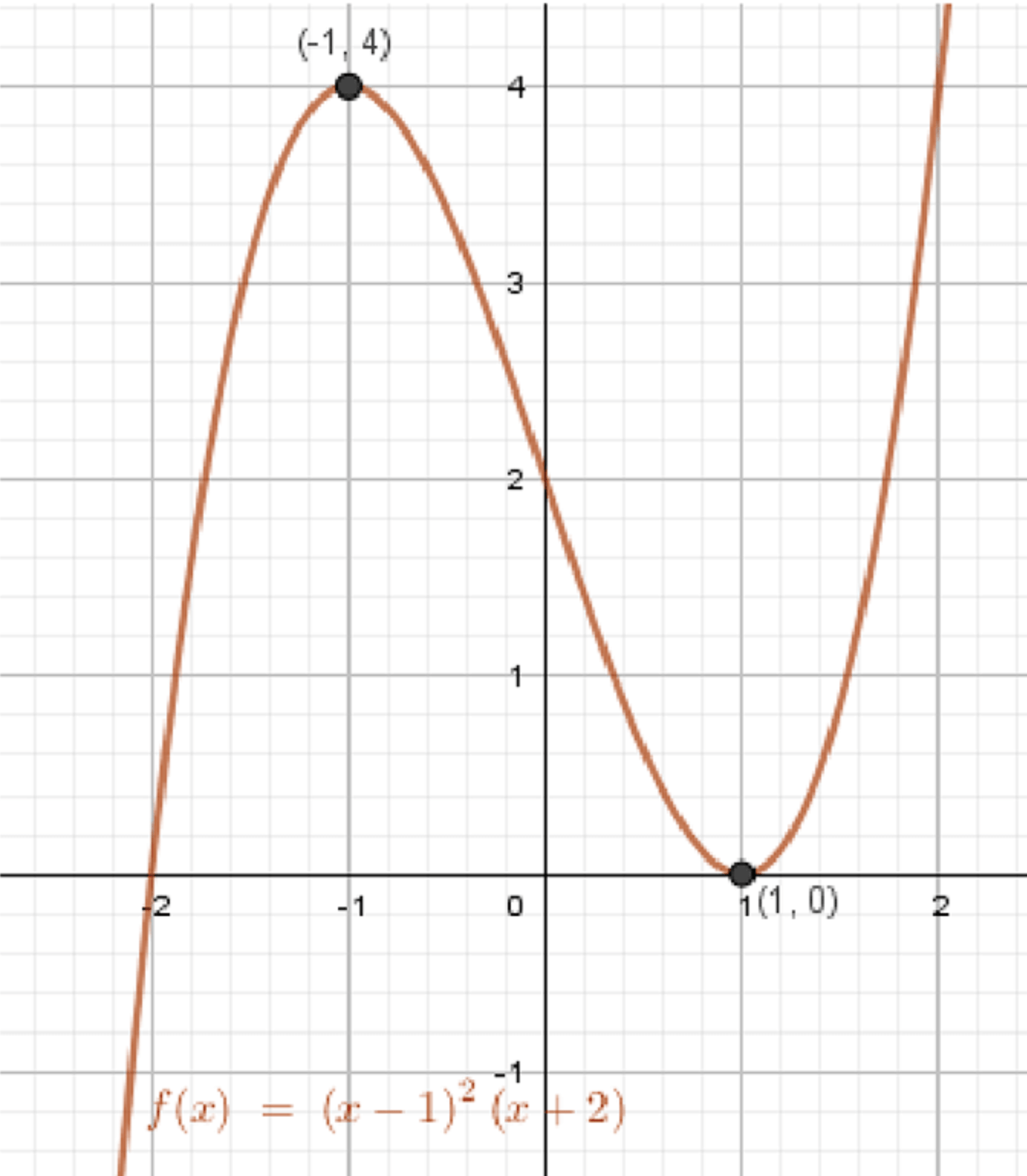
а) $y = (x — 1)^2 \cdot (x + 2)$;

Область определения функции:
$D(y) = (-\infty; +\infty)$;

Производная функции:
$y'(x) = 2 \cdot 1 \cdot (x — 1) \cdot (x + 2) + (x — 1)^2 \cdot (x + 2)’$;
$y'(x) = 2(x — 1)(x + 2) + (x — 1)^2 \cdot 1$;
$y'(x) = (x — 1)(2(x + 2) + (x — 1)) = (x — 1)(3x + 3)$;

Промежуток возрастания:
$(x — 1)(3x + 3) \geq 0$;
$3(x + 1)(x — 1) \geq 0$;
$x \leq -1$ или $x \geq 1$;
$x = 1$ — точка минимума;
$x = -1$ — точка максимума;
$y_{\min} = (1 — 1)^2 \cdot (1 + 2) = 0 \cdot 3 = 0$;
$y_{\max} = (-1 — 1)^2 \cdot (-1 + 2) = (-2)^2 \cdot 1 = 4$;

Координаты некоторых точек:

График функции:

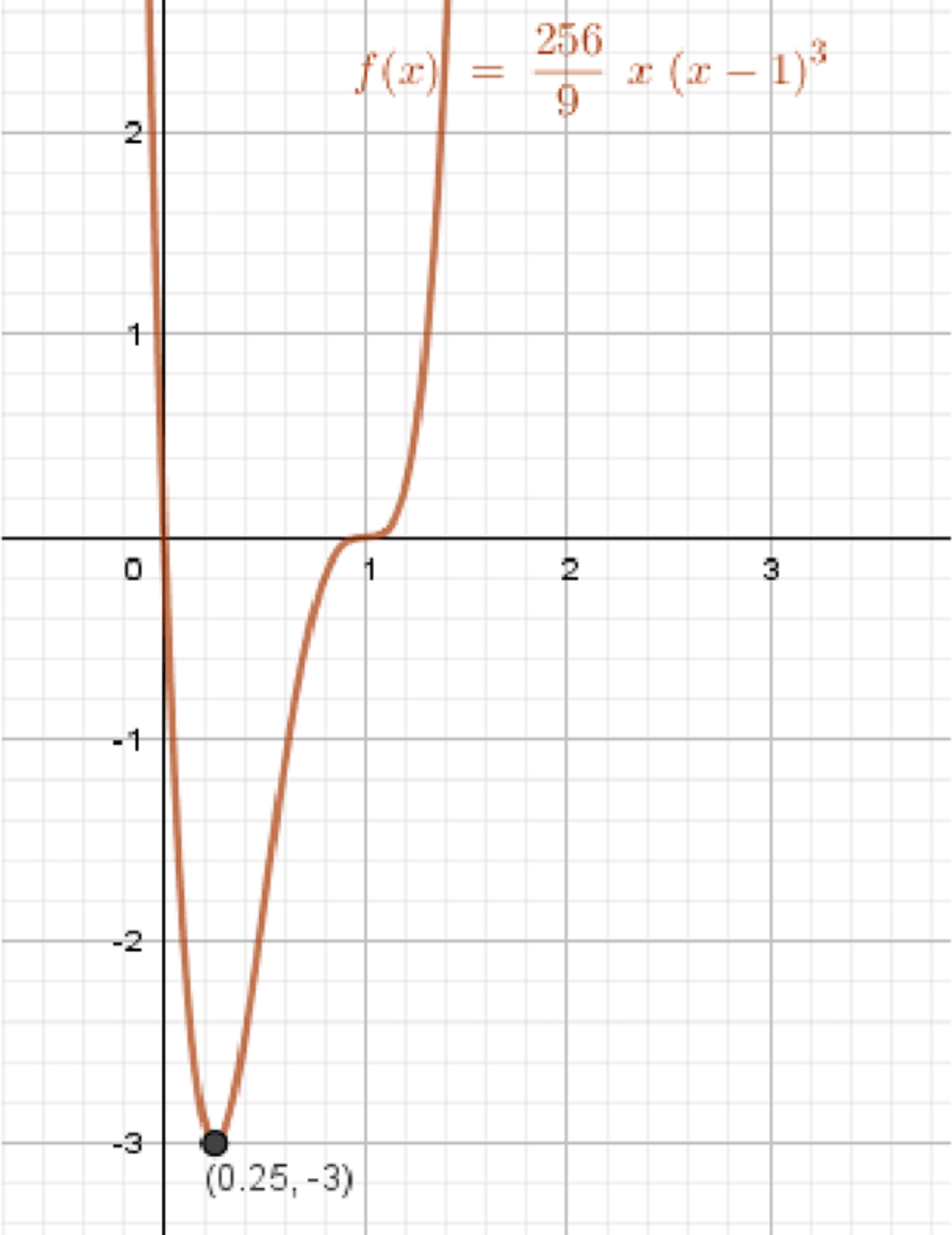
б) $y = \frac{256}{9}x(x — 1)^3$;

Область определения функции:
$D(y) = (-\infty; +\infty)$;

Производная функции:
$y'(x) = \frac{256}{9} \cdot ((x)’ \cdot (x — 1)^3 + x \cdot 3 \cdot 1 \cdot (x — 1)^2)$;
$y'(x) = \frac{256}{9} \cdot (1 \cdot (x — 1)^3 + 3x(x — 1)^2)$;
$y'(x) = \frac{256}{9} \left( (x — 1)^2 \cdot ((x — 1) + 3x) \right) = \frac{256}{9}(x — 1)^2 \cdot (4x — 1)$;

Промежуток возрастания:
$\frac{256}{9}(x — 1)^2 \cdot (4x — 1) \geq 0$;
$4x — 1 \geq 0$;
$4x \geq 1$;
$x \geq 0{,}25$;
$x = 1$ — стационарная точка;
$x = 0{,}25$ — точка минимума;
$y_{\min} = \frac{256}{9} \cdot 0{,}25 \cdot (0{,}25 — 1)^3 = \frac{64 \cdot (-\frac{3}{4})^3}{9} = -\frac{64 \cdot 27}{9 \cdot 64} = -3$;

Координаты некоторых точек:

График функции:

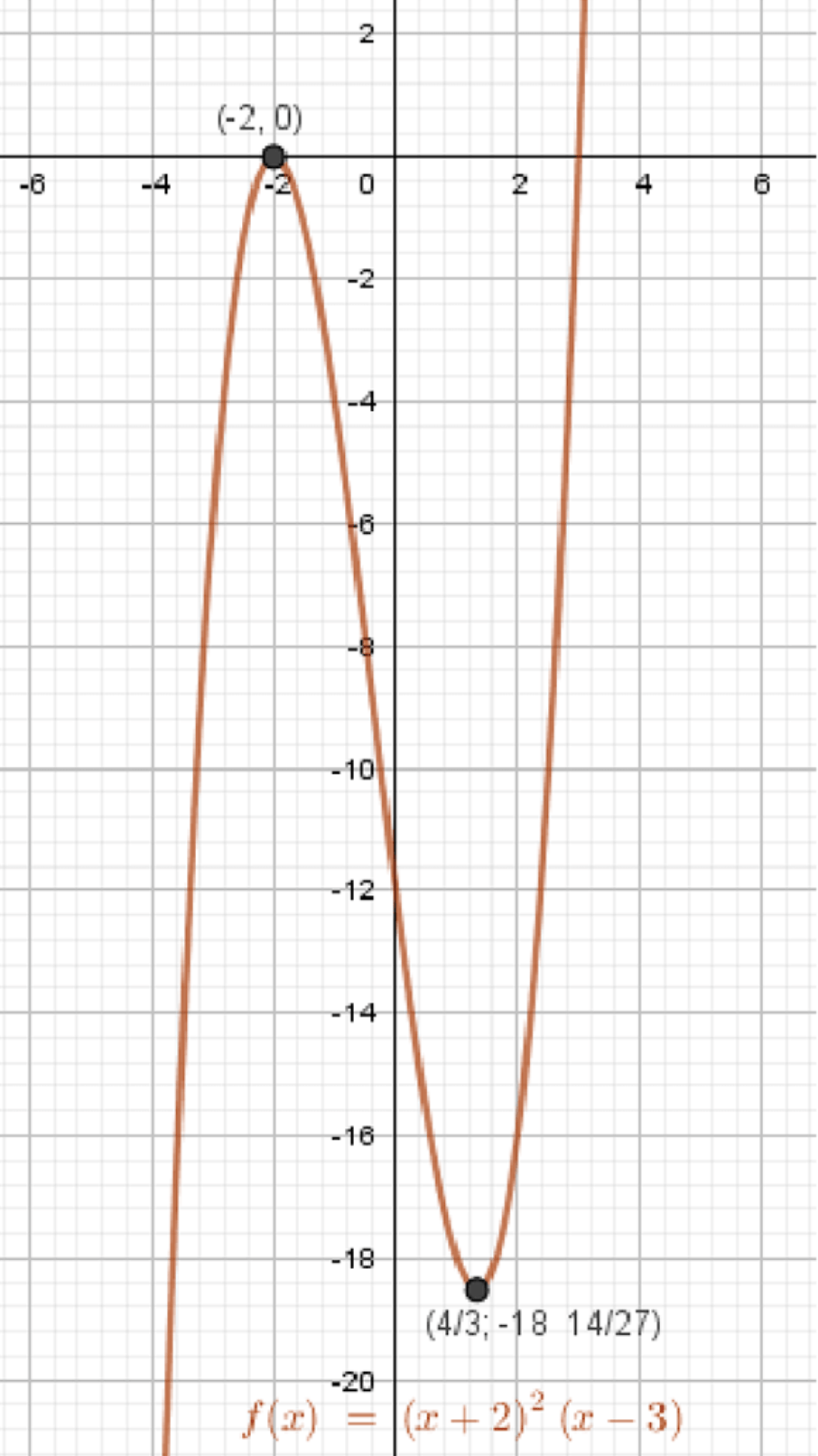
в) $y = (x + 2)^2 \cdot (x — 3)$;

Область определения функции:
$D(y) = (-\infty; +\infty)$;

Производная функции:
$y'(x) = 2 \cdot 1 \cdot (x + 2) \cdot (x — 3) + (x + 2)^2 \cdot (x — 3)’$;
$y'(x) = 2(x + 2)(x — 3) + (x + 2)^2 \cdot 1$;
$y'(x) = (x + 2)(2(x — 3) + (x + 2)) = (x + 2)(3x — 4)$;

Промежуток возрастания:
$(x + 2)(3x — 4) \geq 0$;
$x \leq -2$ или $x \geq 1\frac{1}{3}$;
$x = 1\frac{1}{3}$ — точка минимума;
$x = -2$ — точка максимума;
$y_{\min} = \left(\frac{4}{3} + 2\right)^2 \cdot \left(\frac{4}{3} — 3\right) = \left(\frac{10}{3}\right)^2 \cdot \left(-\frac{5}{3}\right) = -\frac{500}{27} = -18\frac{14}{27}$;
$y_{\max} = (-2 + 2)^2 \cdot (-2 — 3) = 0^2 \cdot (-5) = 0$;

Координаты некоторых точек:

График функции:

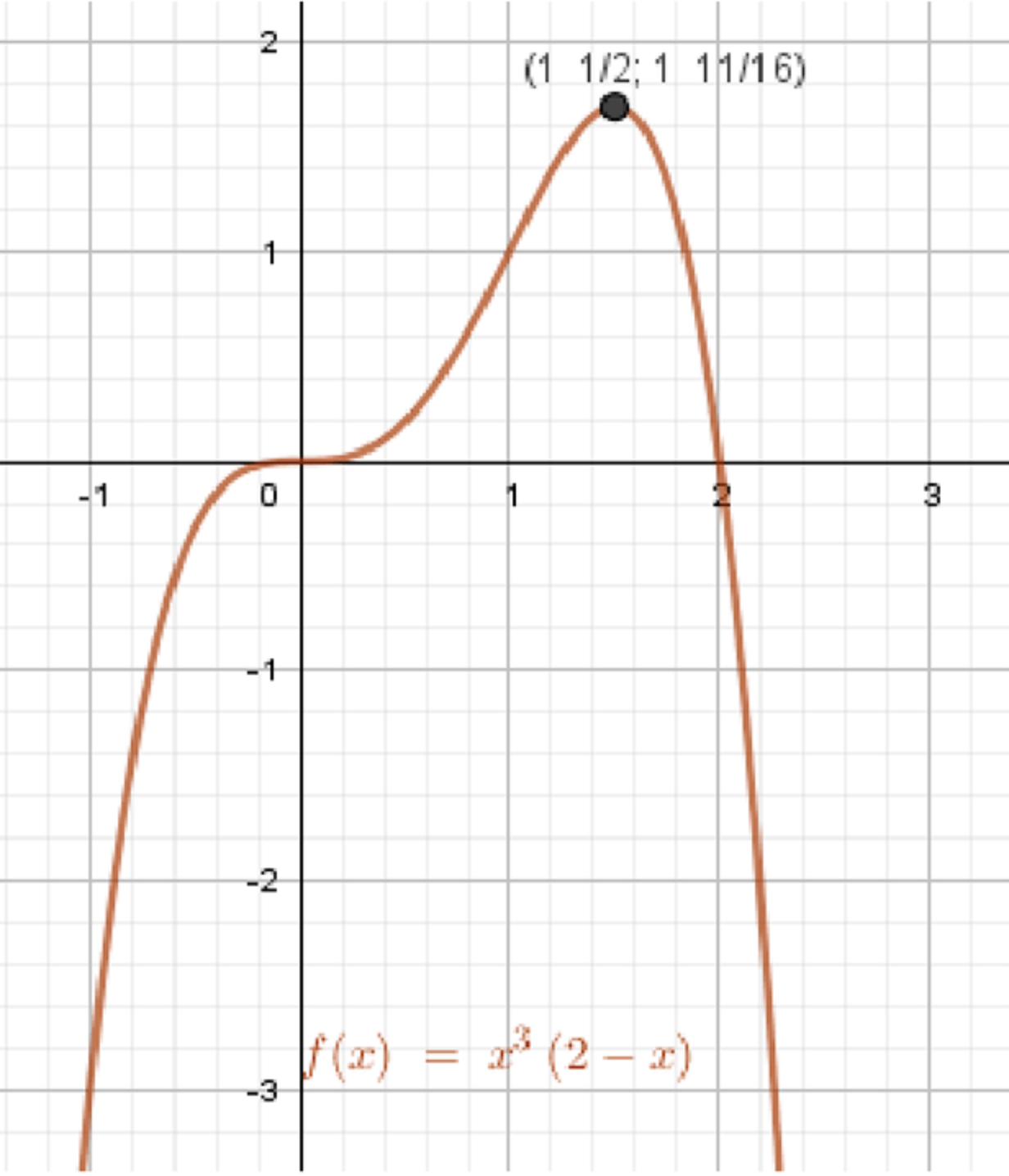
г) $y = x^3 \cdot (2 — x)$;

Область определения функции:
$D(y) = (-\infty; +\infty)$;

Производная функции:
$y'(x) = (x^3)’ \cdot (2 — x) + x^3 \cdot (2 — x)’$;
$y'(x) = 3x^2 \cdot (2 — x) + x^3 \cdot (-1)$;
$y'(x) = 6x^2 — 3x^3 — x^3 = 6x^2 — 4x^3$;

Промежуток возрастания:
$6x^2 — 4x^3 \geq 0$;
$4x^3 — 6x^2 \leq 0$;
$2x^2 \cdot (2x — 3) \leq 0$;
$2x — 3 \leq 0$;
$2x \leq 3$;
$x \leq 1{,}5$;
$x = 0$ — стационарная точка;
$x = 1{,}5$ — точка максимума;
$y_{\max} = (1{,}5)^3 \cdot (2 — 1{,}5) = 3{,}375 \cdot 0{,}5 = 1{,}6875$;

Координаты некоторых точек:

График функции:

а) Функция:

$$y = (x — 1)^2(x + 2)$$

1. Область определения

Функция — это многочлен (произведение степенных выражений), поэтому она определена при всех $x \in \mathbb{R}$.

Ответ:

$$D(y) = (-\infty; +\infty)$$

2. Найдём производную функции

Используем правило произведения:

$$y = f(x) \cdot g(x), \quad f(x) = (x — 1)^2,\quad g(x) = (x + 2)$$

Тогда:

$$y’ = f'(x)g(x) + f(x)g'(x)$$

Вычислим производные:

• $f'(x) = 2(x — 1)$
• $g'(x) = 1$

Подставим:

$$y'(x) = 2(x — 1)(x + 2) + (x — 1)^2(1)$$

Вынесем общий множитель $(x — 1)$:

$$y'(x) = (x — 1)\left[2(x + 2) + (x — 1)\right] = (x — 1)(3x + 3)$$

Формула производной:

$$y'(x) = (x — 1)(3x + 3)$$

3. Исследование производной

Решим неравенство:

$$y'(x) = (x — 1)(3x + 3) \geq 0$$

Равносильно:

$$(x — 1)(x + 1) \geq 0$$

Точки смены знака: $x = -1$ и $x = 1$
Знаки на промежутках:

• $x < -1$: оба множителя отрицательные ⇒ знак $+$
• $-1 < x < 1$: разные знаки ⇒ знак $—$
• $x > 1$: оба положительные ⇒ знак $+$

Промежутки:

• Функция возрастает при: $x \leq -1$ и $x \geq 1$
• Функция убывает при: $-1 \leq x \leq 1$

Точки экстремума:

• $x = -1$ — локальный максимум
• $x = 1$ — локальный минимум

4. Значения функции в критических точках

Минимум:

$$y(1) = (1 — 1)^2 \cdot (1 + 2) = 0 \cdot 3 = 0$$

Максимум:

$$y(-1) = (-1 — 1)^2 \cdot (-1 + 2) = 4 \cdot 1 = 4$$

5. Дополнительные точки

6. Словесное описание графика

• График проходит через точки: $(-2, 0)$, $(0, 2)$, $(1, 0)$, $(2, 4)$
• Имеет максимум в точке $(-1, 4)$
• Имеет минимум в точке $(1, 0)$
• График убывает между $x = -1$ и $x = 1$, возрастает за пределами этих точек
• Поведение похоже на кубическую кривую, с одним максимумом и одним минимумом

б) Функция:

$$y = \frac{256}{9}x(x — 1)^3$$

1. Область определения

Произведение степенных выражений ⇒ определена при всех $x$

Ответ:

$$D(y) = (-\infty; +\infty)$$

2. Производная

Применим правило произведения:

$$y = \frac{256}{9} \cdot x \cdot (x — 1)^3 \Rightarrow y’ = \frac{256}{9} \left[ (x — 1)^3 + x \cdot 3(x — 1)^2 \right]$$

Вынесем общий множитель:

$$y'(x) = \frac{256}{9} (x — 1)^2 \cdot \left[(x — 1) + 3x\right] = \frac{256}{9}(x — 1)^2(4x — 1)$$

3. Исследование производной

Так как $(x — 1)^2 \geq 0$, знак производной зависит от $4x — 1$

• $y’ \geq 0$ при $4x — 1 \geq 0 \Rightarrow x \geq \frac{1}{4}$

Следовательно:

• Функция убывает на $(-\infty; \frac{1}{4}]$
• Функция возрастает на $[\frac{1}{4}; +\infty)$

4. Критическая точка — минимум

$$x = \frac{1}{4}, \quad x — 1 = -\frac{3}{4}$$ $$y = \frac{256}{9} \cdot \frac{1}{4} \cdot \left(-\frac{3}{4}\right)^3 = \frac{256}{9} \cdot \frac{1}{4} \cdot \left(-\frac{27}{64}\right) = -3$$

5. Дополнительные точки

6. Описание графика

• Имеет минимум в точке $x = \frac{1}{4}, y = -3$
• Проходит через точки $x = 0$ и $x = 1$ с $y = 0$
• Убывает до $x = 0.25$, затем возрастает
• График похож на S-образную кривую, с изгибом в точке минимума

в) Функция:

$$y = (x + 2)^2(x — 3)$$

1. Область определения

Функция — многочлен ⇒ определена при всех $x$

$$D(y) = (-\infty; +\infty)$$

2. Производная

$$y'(x) = 2(x + 2)(x — 3) + (x + 2)^2 \cdot 1$$

Вынесем $(x + 2)$:

$$y'(x) = (x + 2)\left[2(x — 3) + (x + 2)\right] = (x + 2)(3x — 4)$$

3. Исследование производной

$$(x + 2)(3x — 4) \geq 0$$

Нули: $x = -2$, $x = \frac{4}{3}$

Промежутки:

• $x \leq -2$: положительно
• $-2 < x < \frac{4}{3}$: отрицательно
• $x \geq \frac{4}{3}$: положительно

Функция:

• возрастает на $(-\infty; -2] \cup [\frac{4}{3}; +\infty)$
• убывает на $[-2; \frac{4}{3}]$

4. Экстремумы

Максимум:

$$x = -2, \quad y = 0$$

Минимум:

$$x = \frac{4}{3}, \quad (x + 2)^2 = \left(\frac{10}{3}\right)^2 = \frac{100}{9}, \quad x — 3 = -\frac{5}{3}$$ $$y = \frac{100}{9} \cdot \left(-\frac{5}{3}\right) = -\frac{500}{27} \approx -18.52$$

5. Таблица значений

6. Описание графика

• Максимум: $(-2, 0)$
• Минимум: $\left(\frac{4}{3}, -\frac{500}{27} \right)$
• График убывает между этими точками, затем возрастает
• Форма — несимметричная S-образная кривая

г) Функция:

$$y = x^3(2 — x)$$

1. Область определения

Многочлен ⇒ определена всюду

$$D(y) = (-\infty; +\infty)$$

2. Производная

$$y'(x) = 3x^2(2 — x) + x^3(-1) = 6x^2 — 3x^3 — x^3 = 6x^2 — 4x^3$$

3. Исследование производной

$$6x^2 — 4x^3 \geq 0 \Rightarrow 2x^2(3 — 2x) \geq 0$$

Положительно при:

• $3 — 2x \geq 0 \Rightarrow x \leq 1.5$

Функция:

• возрастает на $(-\infty; 1.5]$
• убывает на $[1.5; +\infty)$

4. Экстремум

Максимум:

$$x = 1.5, \quad y = (1.5)^3 \cdot (2 — 1.5) = 3.375 \cdot 0.5 = 1.6875$$

5. Таблица значений

6. Описание графика

• График возрастает до $x = 1.5$, потом убывает
• Имеет максимум в точке $(1.5, 1.6875)$
• Пересекает ось $x$ в точках $x = 0$ и $x = 2$
• Форма: кубическая кривая с перегибом, с максимумом посередине