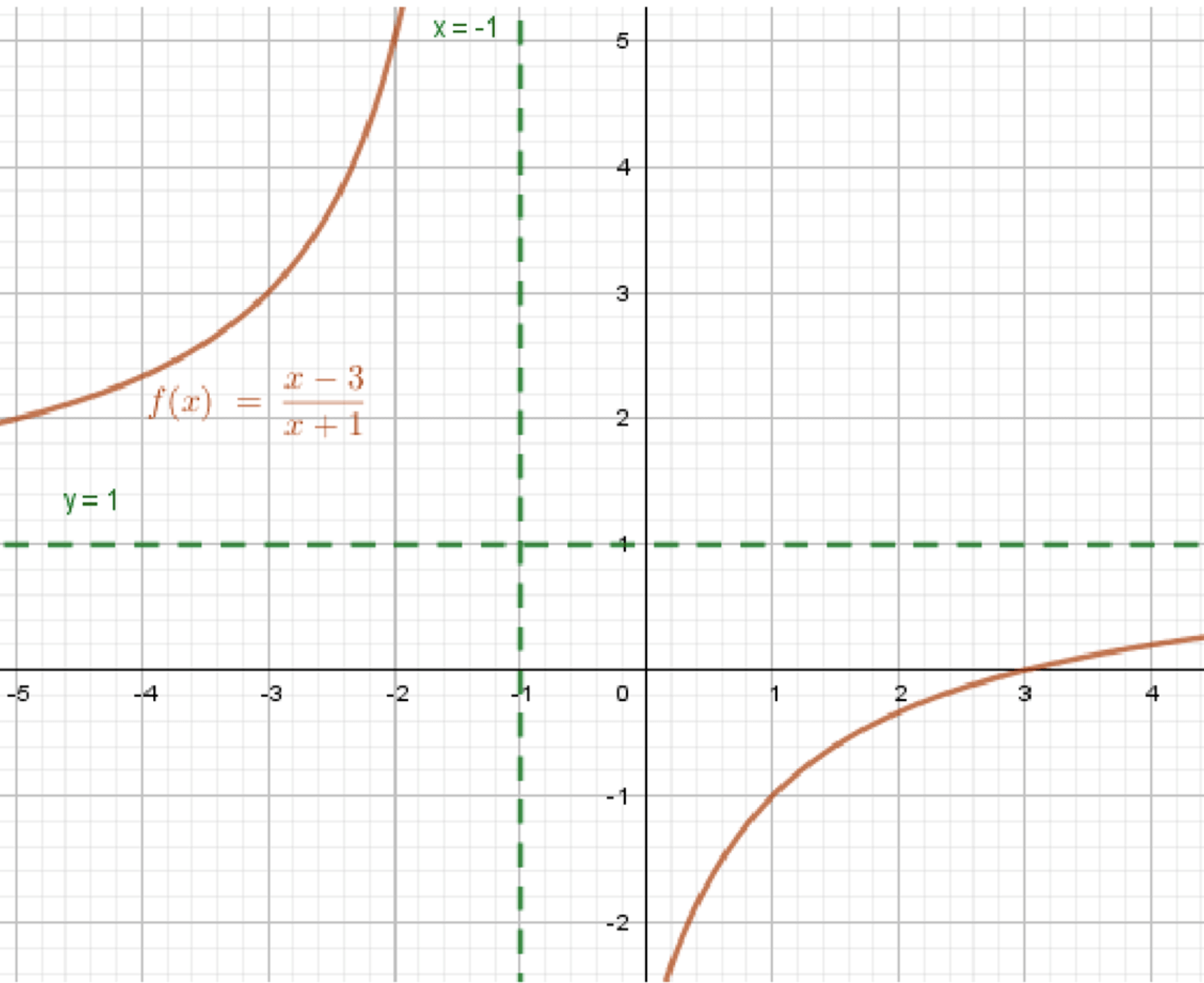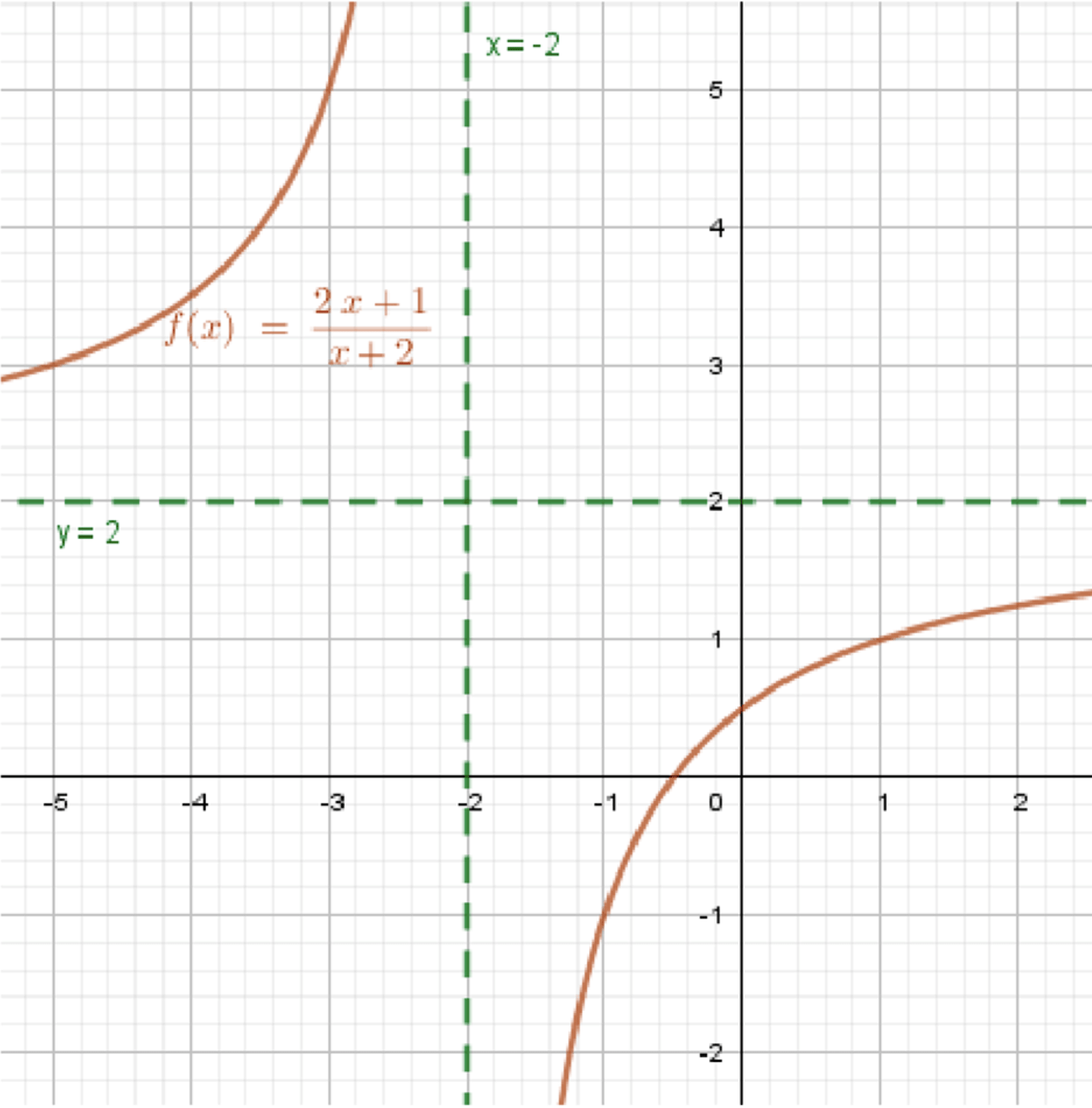ГДЗ 10-11 Класс Номер 31.9 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

а) $y = \dfrac{x + 2}{x — 3}$

б) $y = \dfrac{3x — 4}{x — 2}$

в) $y = \dfrac{x — 3}{x + 1}$

г) $y={\displaystyle \frac{2x+1}{x+2}}$

Построить график функции:

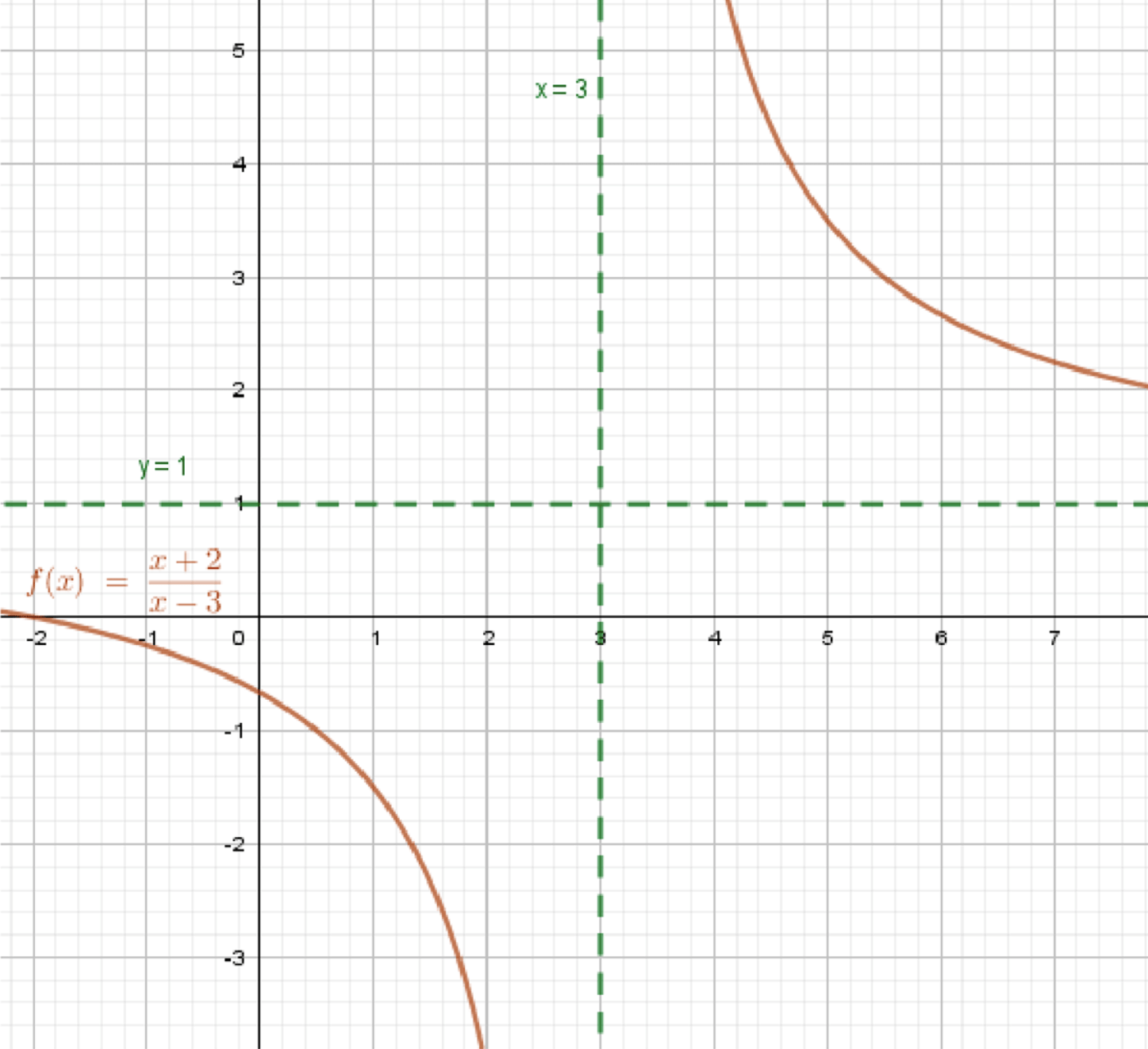
а) $y = \dfrac{x + 2}{x — 3}$

Область определения функции:
$x — 3 \ne 0$;
$x \ne 3$;
$D(y) = (-\infty; 3) \cup (3; +\infty)$;

Уравнения асимптот:
$x = 3$;
$y = \lim_{x \to \infty} \dfrac{x + 2}{x — 3} = \lim_{x \to \infty} \dfrac{1 + \dfrac{2}{x}}{1 — \dfrac{3}{x}} = \dfrac{1 + 0}{1 — 0} = \dfrac{1}{1} = 1$;

Производная функции:
$y'(x) = \dfrac{(x + 2)’ \cdot (x — 3) — (x + 2) \cdot (x — 3)’}{(x — 3)^2}$;
$y'(x) = \dfrac{1 \cdot (x — 3) — (x + 2) \cdot 1}{(x — 3)^2} = \dfrac{x — 3 — x — 2}{(x — 3)^2} = \dfrac{-5}{(x — 3)^2} < 0$;
Функция убывает на всей области определения;

Координаты некоторых точек:

График функции:

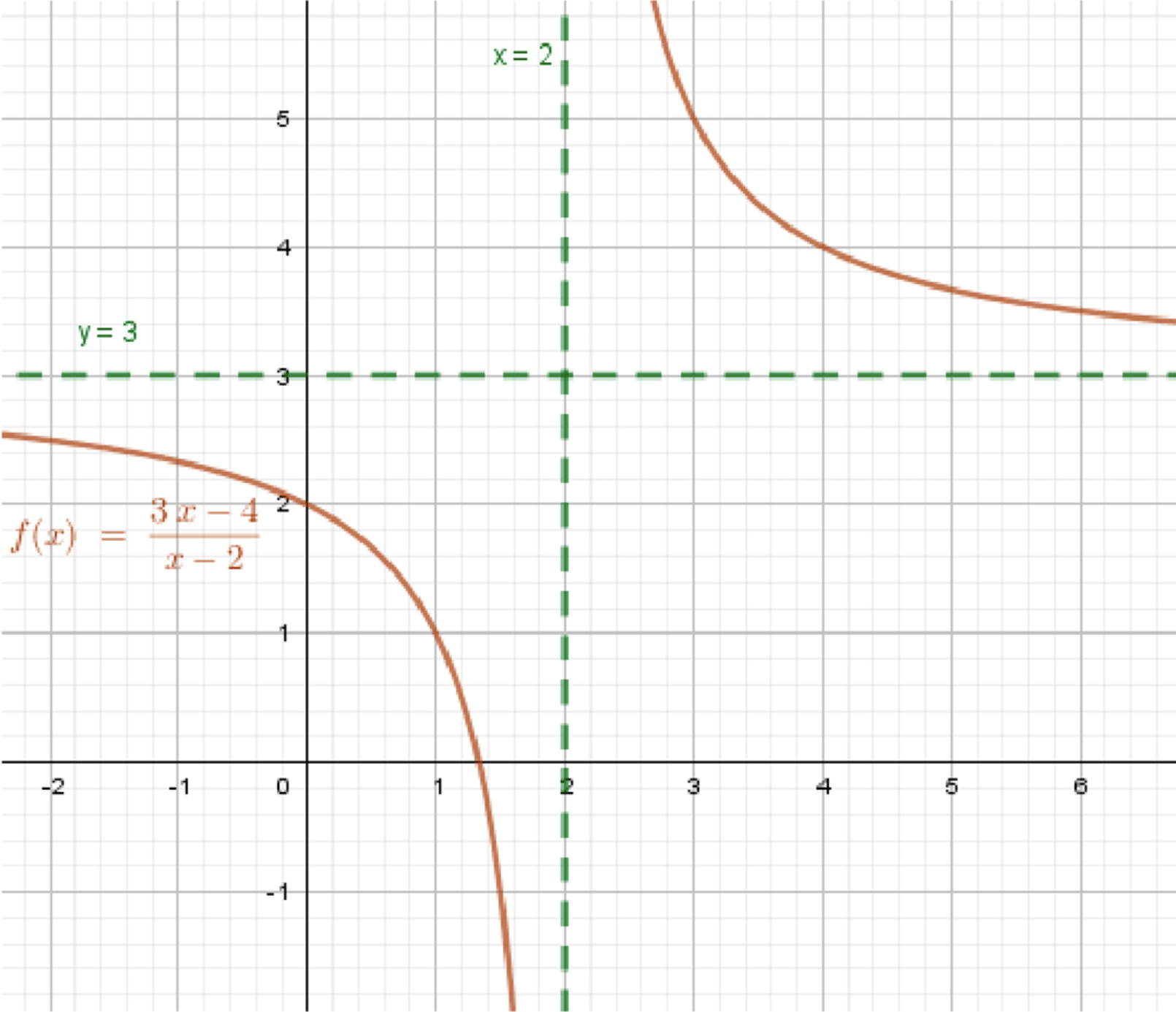
б) $y = \dfrac{3x — 4}{x — 2}$

Область определения функции:
$x — 2 \ne 0$;
$x \ne 2$;
$D(y) = (-\infty; 2) \cup (2; +\infty)$;

Уравнения асимптот:
$x = 2$;
$y = \lim_{x \to \infty} \dfrac{3x — 4}{x — 2} = \lim_{x \to \infty} \dfrac{3 — \dfrac{4}{x}}{1 — \dfrac{2}{x}} = \dfrac{3 — 0}{1 — 0} = \dfrac{3}{1} = 3$;

Производная функции:
$y'(x) = \dfrac{(3x — 4)’ \cdot (x — 2) — (3x — 4) \cdot (x — 2)’}{(x — 2)^2}$;
$y'(x) = \dfrac{3 \cdot (x — 2) — (3x — 4) \cdot 1}{(x — 2)^2} = \dfrac{3x — 6 — 3x + 4}{(x — 2)^2} = \dfrac{-2}{(x — 2)^2} < 0$;
Функция убывает на всей области определения;

Координаты некоторых точек:

График функции:

в) $y = \dfrac{x — 3}{x + 1}$

Область определения функции:
$x + 1 \ne 0$;
$x \ne -1$;
$D(y) = (-\infty; -1) \cup (-1; +\infty)$;

Уравнения асимптот:
$x = -1$;
$y = \lim_{x \to \infty} \dfrac{x — 3}{x + 1} = \lim_{x \to \infty} \dfrac{1 — \dfrac{3}{x}}{1 + \dfrac{1}{x}} = \dfrac{1 — 0}{1 + 0} = \dfrac{1}{1} = 1$;

Производная функции:
$y'(x) = \dfrac{(x — 3)’ \cdot (x + 1) — (x — 3) \cdot (x + 1)’}{(x + 1)^2}$;
$y'(x) = \dfrac{1 \cdot (x + 1) — (x — 3) \cdot 1}{(x + 1)^2} = \dfrac{x + 1 — x + 3}{(x + 1)^2} = \dfrac{4}{(x + 1)^2} > 0$;
Функция возрастает на всей области определения;

Координаты некоторых точек:

График функции:

г) $y = \dfrac{2x + 1}{x + 2}$

Область определения функции:
$x + 2 \ne 0$;
$x \ne -2$;
$D(y) = (-\infty; -2) \cup (-2; +\infty)$;

Уравнения асимптот:
$x = -2$;
$y = \lim_{x \to \infty} \dfrac{2x + 1}{x + 2} = \lim_{x \to \infty} \dfrac{2 + \dfrac{1}{x}}{1 + \dfrac{2}{x}} = \dfrac{2 + 0}{1 + 0} = \dfrac{2}{1} = 2$;

Производная функции:
$y'(x) = \dfrac{(2x + 1)’ \cdot (x + 2) — (2x + 1) \cdot (x + 2)’}{(x + 2)^2}$;
$y'(x) = \dfrac{2 \cdot (x + 2) — (2x + 1) \cdot 1}{(x + 2)^2} = \dfrac{2x + 4 — 2x — 1}{(x + 2)^2} = \dfrac{3}{(x + 2)^2} > 0$;
Функция возрастает на всей области определения;

Координаты некоторых точек:

График функции:

а) $y = \dfrac{x + 2}{x — 3}$

1. Область определения

Дробь определена при $x — 3 \ne 0 \Rightarrow x \ne 3$.
Ответ:
$D(y) = (-\infty; 3) \cup (3; +\infty)$

2. Асимптоты

• Вертикальная асимптота:
  При $x = 3$, знаменатель обращается в 0. График стремится к бесконечности.
  Ответ: $x = 3$
• Горизонтальная асимптота:

  $$\lim_{x \to \infty} \frac{x + 2}{x — 3} = \frac{1}{1} = 1$$

  Ответ: $y = 1$

3. Производная

$$y'(x) = \frac{(x + 2)’ \cdot (x — 3) — (x + 2) \cdot (x — 3)’}{(x — 3)^2} = \frac{1 \cdot (x — 3) — (x + 2) \cdot 1}{(x — 3)^2} = \frac{-5}{(x — 3)^2}$$

Анализ производной:

• Знаменатель положительный при любом $x \ne 3$
• Числитель — постоянное число $-5$
• Следовательно, $y'(x) < 0$ на всей области определения

Вывод: функция строго убывает на $(-\infty; 3) \cup (3; +\infty)$

4. Поведение графика

• Функция имеет разрыв II рода в точке $x = 3$
• Стремится к бесконечности при $x \to 3^\pm$
• При больших значениях $x \to \pm\infty$, $y \to 1$
• Функция нигде не обращается в максимум/минимум, так как она монотонна

5. Таблица значений

б) $y = \dfrac{3x — 4}{x — 2}$

1. Область определения

$x — 2 \ne 0 \Rightarrow x \ne 2$
Ответ:
$D(y) = (-\infty; 2) \cup (2; +\infty)$

2. Асимптоты

• Вертикальная: $x = 2$
• Горизонтальная:

  $$\lim_{x \to \infty} \frac{3x — 4}{x — 2} = \frac{3}{1} = 3$$

Ответ:
Вертикальная: $x = 2$, Горизонтальная: $y = 3$

3. Производная

$$y'(x) = \frac{(3x — 4)’ \cdot (x — 2) — (3x — 4) \cdot (x — 2)’}{(x — 2)^2} = \frac{3(x — 2) — (3x — 4)}{(x — 2)^2} = \frac{-2}{(x — 2)^2}$$

Вывод: Производная отрицательная, функция строго убывает на всей области определения

4. Поведение функции

• Разрыв в $x = 2$
• Монотонное убывание на обеих частях
• При $x \to \pm\infty$, $y \to 3$

5. Таблица значений

в) $y = \dfrac{x — 3}{x + 1}$

1. Область определения

$x + 1 \ne 0 \Rightarrow x \ne -1$
Ответ:
$D(y) = (-\infty; -1) \cup (-1; +\infty)$

2. Асимптоты

• Вертикальная: $x = -1$
• Горизонтальная:

  $$\lim_{x \to \infty} \frac{x — 3}{x + 1} = \frac{1}{1} = 1$$

Ответ:
Вертикальная: $x = -1$, Горизонтальная: $y = 1$

3. Производная

$$y'(x) = \frac{(x — 3)'(x + 1) — (x — 3)(x + 1)’}{(x + 1)^2} = \frac{1(x + 1) — (x — 3)}{(x + 1)^2} = \frac{4}{(x + 1)^2}$$

Вывод: Производная положительная, функция строго возрастает

4. Поведение функции

• Разрыв в точке $x = -1$
• Функция возрастает на обеих частях
• При $x \to \pm\infty$, $y \to 1$

5. Таблица значений

г) $y = \dfrac{2x + 1}{x + 2}$

1. Область определения

$x + 2 \ne 0 \Rightarrow x \ne -2$
Ответ:
$D(y) = (-\infty; -2) \cup (-2; +\infty)$

2. Асимптоты

• Вертикальная: $x = -2$
• Горизонтальная:

  $$\lim_{x \to \infty} \frac{2x + 1}{x + 2} = \frac{2}{1} = 2$$

Ответ:
Вертикальная: $x = -2$, Горизонтальная: $y = 2$

3. Производная

$$y'(x) = \frac{(2x + 1)'(x + 2) — (2x + 1)(x + 2)’}{(x + 2)^2} = \frac{2(x + 2) — (2x + 1)}{(x + 2)^2} = \frac{3}{(x + 2)^2}$$

Вывод: Производная положительная, функция строго возрастает

4. Поведение функции

• Разрыв при $x = -2$
• Возрастает
• Асимптоты: $x = -2$, $y = 2$

5. Таблица значений