ГДЗ 10-11 Класс Номер 32.29 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

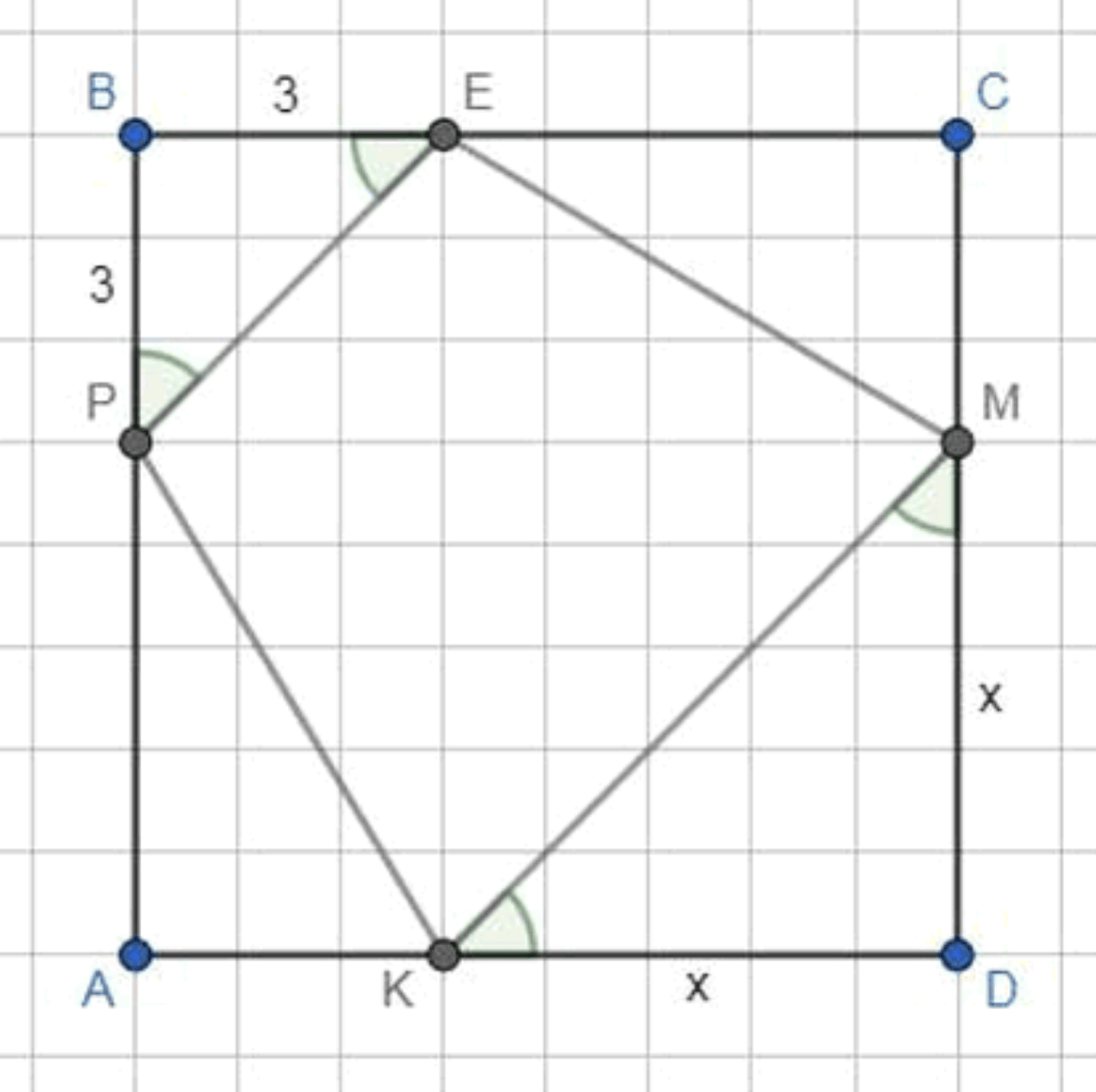
Сторона квадрата ABCD равна 8 см. На сторонах АВ и ВС взяты соответственно точки Р и Е так, что BP = BE = 3 см. На сторонах AD и CD берутся точки соответственно К и М так, что четырёхугольник КРЕМ — трапеция. Чему равна наибольшая площадь такой трапеции?

Дано: $ABCD$ – квадрат; $AB = 8$ см; $BP = BE = 3$ см; $KPEM$ – трапеция;
Найти: наименьшую площадь $KPEM$;

Пусть $MD = x$, отобразим условие задачи:

Рассмотрим прямоугольный треугольник $PBE$:
$PB = BE = 3$;
$\angle BPE = \angle BEP = 45^\circ$;
$S_{BPE} = \frac{1}{2} PB \cdot BE = \frac{1}{2} \cdot 3 \cdot 3 = \frac{9}{2}$;

Из условия следует, что $AB \parallel CD$, $BC \parallel AD$, $PE \parallel KM$, значит:
$\angle MKD = \angle BEP = 45^\circ$;
$\angle KMD = \angle BPE = 45^\circ$;

Рассмотрим прямоугольный треугольник $MDK$:
$MD = DK = x$;
$S_{MDK} = \frac{1}{2} MD \cdot DK = \frac{1}{2} \cdot x \cdot x = \frac{x^2}{2}$;

Рассмотрим прямоугольные треугольники $PAK$ и $ECM$:
$PA = EC = 8 — 3 = 5$;
$KA = MC = 8 — x$;
$S_{PAK} = S_{ECM} = \frac{1}{2} PA \cdot KA = \frac{1}{2} \cdot 5 \cdot (8 — x) = 20 — \frac{5x}{2}$;

Площадь искомой трапеции:
$S(x) = S_{ABCD} — S_{BPE} — S_{MDK} — S_{PAK} — S_{ECM}$;
$S(x) = 8 \cdot 8 — \frac{9}{2} — \frac{x^2}{2} — \left(20 — \frac{5x}{2}\right) — \left(20 — \frac{5x}{2}\right)$;
$S(x) = 64 — 4,5 — 0,5x^2 — 40 + 5x = 5x + 19,5 — 0,5x^2$;

Производная функции:
$S'(x) = (5x + 19,5)’ — 0,5(x^2)’ = 5 — 0,5 \cdot 2x = 5 — x$;

Промежуток возрастания:
$5 — x \geq 0$;
$x \leq 5$;

Точка максимума:
$x_{\max} = 5$;
$S(5) = 5 \cdot 5 + 19,5 — 0,5 \cdot 5^2 = 25 + 19,5 — 12,5 = 32$;

Ответ: $32$ см².

1. Пусть $MD = x$, отобразим условие задачи:

Нам дан квадрат $ABCD$, где $AB = 8$ см. Также даны длины отрезков $BP = BE = 3$ см, а трапеция $KPEM$ включена в эту задачу.

2. Рассмотрим прямоугольный треугольник $PBE$:

У нас есть прямоугольный треугольник $PBE$, где $PB = BE = 3$ см, и угол $\angle BPE = \angle BEP = 45^\circ$. Площадь этого треугольника можно вычислить по формуле для площади прямоугольного треугольника:

$$S_{BPE} = \frac{1}{2} \cdot PB \cdot BE = \frac{1}{2} \cdot 3 \cdot 3 = \frac{9}{2} \text{ см}^2.$$

3. Рассмотрим трапецию $KPEM$:

Из условия задачи известно, что:

• $AB \parallel CD$, $BC \parallel AD$, и $PE \parallel KM$, значит, углы $\angle MKD = \angle BEP = 45^\circ$ и $\angle KMD = \angle BPE = 45^\circ$.

Это важное условие для дальнейших расчетов.

4. Рассмотрим прямоугольный треугольник $MDK$:

Мы знаем, что $MD = DK = x$, так как $M$ и $D$ симметричны относительно прямой $AB$, и трапеция имеет эти стороны равными. Площадь прямоугольного треугольника $MDK$:

$$S_{MDK} = \frac{1}{2} \cdot MD \cdot DK = \frac{1}{2} \cdot x \cdot x = \frac{x^2}{2} \text{ см}^2.$$

5. Рассмотрим прямоугольные треугольники $PAK$ и $ECM$:

Длины сторон:

• $PA = EC = 8 — 3 = 5$ см (так как $P$ и $E$ лежат на сторонах квадрата, а $BP = BE = 3$ см).
• $KA = MC = 8 — x$ см (так как $K$ и $M$ находятся на стороне квадрата, отнимаем длину $x$).

Площадь прямоугольного треугольника $PAK$:

$$S_{PAK} = \frac{1}{2} \cdot PA \cdot KA = \frac{1}{2} \cdot 5 \cdot (8 — x) = 20 — \frac{5x}{2} \text{ см}^2.$$

Аналогичная площадь для треугольника $ECM$:

$$S_{ECM} = \frac{1}{2} \cdot EC \cdot MC = \frac{1}{2} \cdot 5 \cdot (8 — x) = 20 — \frac{5x}{2} \text{ см}^2.$$

6. Площадь искомой трапеции $KPEM$:

Площадь трапеции $KPEM$ можно найти, вычитая площади всех фигур, которые находятся внутри квадрата $ABCD$. Площадь квадрата:

$$S_{ABCD} = 8 \cdot 8 = 64 \text{ см}^2.$$

Итак, площадь трапеции:

$$S(x) = S_{ABCD} — S_{BPE} — S_{MDK} — S_{PAK} — S_{ECM}.$$

Подставим все найденные площади:

$$S(x) = 64 — \frac{9}{2} — \frac{x^2}{2} — \left(20 — \frac{5x}{2}\right) — \left(20 — \frac{5x}{2}\right).$$

Упростим выражение:

$$S(x) = 64 — 4,5 — \frac{x^2}{2} — 20 + \frac{5x}{2} — 20 + \frac{5x}{2}.$$ $$S(x) = 64 — 44,5 — \frac{x^2}{2} + 5x.$$ $$S(x) = 19,5 + 5x — \frac{x^2}{2}.$$

7. Находим производную функции площади:

Найдем производную функции площади $S(x)$ по переменной $x$:

$$S'(x) = \frac{d}{dx} \left(19,5 + 5x — \frac{x^2}{2}\right) = 5 — x.$$

8. Определим промежуток возрастания функции:

Найдем промежуток, на котором площадь $S(x)$ возрастает. Для этого решим неравенство:

$$S'(x) = 5 — x \geq 0.$$

Отсюда:

$$x \leq 5.$$

9. Найдем точку максимума:

Точка максимума будет достигаться, когда $x = 5$. Подставим $x = 5$ в выражение для площади:

$$S(5) = 19,5 + 5 \cdot 5 — \frac{5^2}{2} = 19,5 + 25 — \frac{25}{2} = 19,5 + 25 — 12,5 = 32 \text{ см}^2.$$

Ответ:

Наименьшая площадь трапеции $KPEM$ равна $\boxed{32}$ см².