ГДЗ 10-11 Класс Номер 32.37 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Из прямоугольной трапеции с основаниями а и b и высотой h вырезают прямоугольник наибольшей площади.

Чему равна эта площадь, если:

а) а = 80, b = 60, h = 100;

б) а = 24, b = 8, h = 12?

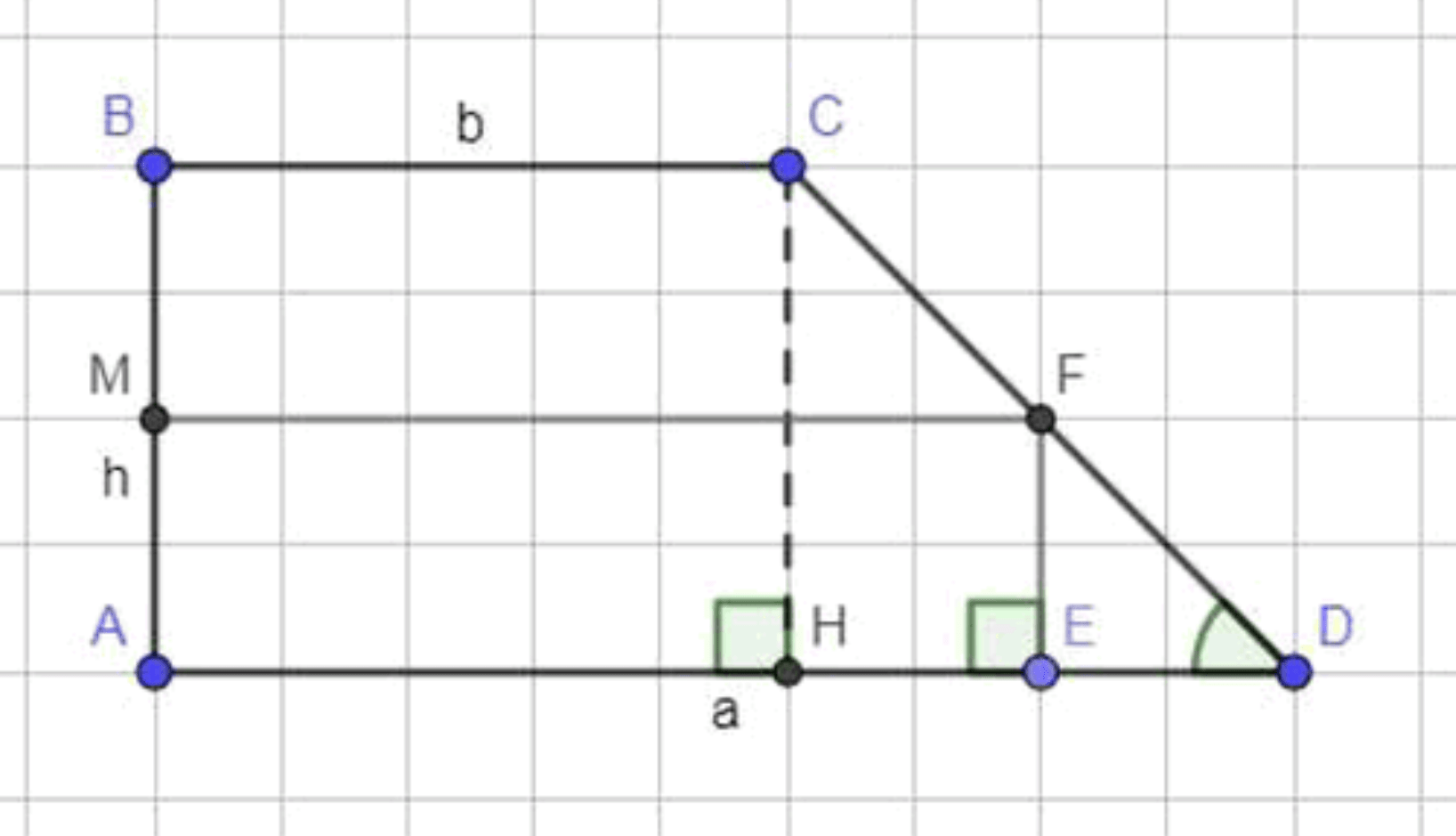
Отобразим условие задачи:

Дано: $ABCD$ — прямоугольная трапеция; $AB = h$; $AD = a$; $BC = b$;
Найти: наибольшую площадь вырезанного прямоугольника;

Решение:

Опустим высоту $CH$ данной трапеции, тогда:
$CH = AB = h$;

Четырехугольник $ABCH$ является прямоугольником, значит:
$AH = BC = b$;
$HD = AD — AH = a — b$;

Пусть точки $A$, $E \in AD$, $F \in CD$ и $M \in AB$ — вершины искомого прямоугольника, при этом $AE = x$, тогда:
$ED = AD — AE = a — x$;

Прямоугольные $\triangle CHD \sim \triangle FED$ по общему острому углу $D$, значит:
$\frac{ED}{HD} = \frac{FE}{CH}$, отсюда
$FE = \frac{ED \cdot CH}{HD} = \frac{(a — x) \cdot h}{a — b} = \frac{ah — xh}{a — b}$;

Площадь прямоугольника $AMFE$:
$S(x) = AE \cdot FE = x \cdot \frac{ah — xh}{a — b} = \frac{ahx — hx^2}{a — b}$;

Производная функции:
$S'(x) = \frac{1}{a — b} \cdot (ah(x)’ — h(x^2)’) = \frac{ah — 2hx}{a — b}$;

Промежуток возрастания:
$\frac{ah — 2hx}{a — b} \geq 0$;
$ah — 2hx \geq 0$;
$h(a — 2x) \geq 0$;
$a — 2x \geq 0$;
$a \geq 2x$, отсюда $x \leq \frac{a}{2}$;

Наибольшее значение функции составляет:
$S\left(\frac{a}{2}\right) = \left(ah \cdot \frac{a}{2} — h \cdot \frac{a^2}{4}\right) : (a — b) = \left(\frac{a^2h}{2} — \frac{a^2h}{4}\right) : (a — b) = \frac{a^2h}{4a — 4b}$;

Но если $\frac{a}{2} < b$, тогда наибольшее значение функции равно:
$S(b) = \frac{ahb — hb^2}{a — b} = \frac{hb(a — b)}{a — b} = hb$;

а) Если $a = 80$, $b = 60$ и $h = 100$:
$\frac{a}{2} = \frac{80}{2} = 40 < 60$;
$S(60) = 100 \cdot 60 = 6000$;

б) Если $a = 24$, $b = 8$ и $h = 12$:
$\frac{a}{2} = \frac{24}{2} = 12 > 8$;
$S\left(\frac{24}{2}\right) = \frac{24^2 \cdot 12}{4 \cdot 24 — 4 \cdot 8} = \frac{576 \cdot 12}{96 — 32} = \frac{6912}{64} = 108$;

Ответ: а) 6000; б) 108.

Дана прямоугольная трапеция $ABCD$, у которой:

• $AB = h$ — высота трапеции,
• $AD = a$ — левая боковая сторона,
• $BC = b$ — правая боковая сторона.

Требуется найти наибольшую площадь прямоугольника, который можно вырезать внутри этой трапеции.

Шаг 1. Построим вспомогательные элементы

Опустим перпендикуляр $CH$ из точки $C$ на прямую $AD$. Так как трапеция прямоугольная, то:

$$CH = AB = h$$

Четырехугольник $ABCH$ является прямоугольником (все углы прямые). Тогда:

$$AH = BC = b, \quad HD = AD — AH = a — b$$

Шаг 2. Построим произвольный прямоугольник внутри трапеции

Пусть точки $A$, $E$ лежат на стороне $AD$, $F$ — на $CD$, $M$ — на $AB$, и четырехугольник $AMFE$ — искомый прямоугольник.

Пусть:

$$AE = x \quad \Rightarrow \quad ED = a — x$$

Шаг 3. Найдём длину стороны $FE$ прямоугольника $AMFE$

Рассмотрим подобные прямоугольные треугольники:

• $\triangle CHD$ (внешний),
• $\triangle FED$ (внутренний).

Они подобны по общему углу при вершине $D$ и по равенству углов, так как оба прямоугольные.

По подобию треугольников:

$$\frac{ED}{HD} = \frac{FE}{CH} \quad \Rightarrow \quad FE = \frac{ED \cdot CH}{HD}$$

Подставим:

$$FE = \frac{(a — x) \cdot h}{a — b}$$

Шаг 4. Выражение для площади прямоугольника

Площадь прямоугольника $S(x)$ равна произведению его сторон $AE = x$ и $FE$, получаем:

$$S(x) = x \cdot \frac{(a — x)h}{a — b} = \frac{h(ax — x^2)}{a — b}$$

Шаг 5. Найдём максимум функции площади

Функция:

$$S(x) = \frac{h(ax — x^2)}{a — b}$$

Это квадратичная функция с ветвями, направленными вниз ($-x^2$).

Найдем её производную:

$$S'(x) = \frac{h(a — 2x)}{a — b}$$

Приравниваем производную к нулю:

$$\frac{h(a — 2x)}{a — b} = 0 \quad \Rightarrow \quad a — 2x = 0 \quad \Rightarrow \quad x = \frac{a}{2}$$

Шаг 6. Проверим геометрическую допустимость

Необходимо, чтобы прямоугольник полностью помещался в трапеции. Сторона $FE$ должна быть не длиннее основания $BC = b$, и правая вершина прямоугольника не должна выходить за пределы основания.

То есть необходимо, чтобы:

$$x \leq b$$

Проверим условие:

• Если $\frac{a}{2} \leq b$, то максимум действительно достигается при $x = \frac{a}{2}$.
• Если $\frac{a}{2} > b$, то точка $x = \frac{a}{2}$ выходит за границу допустимого отрезка, и максимум достигается при $x = b$.

Шаг 7. Подстановка значений

Случай 1: $\frac{a}{2} \leq b$

Подставим $x = \frac{a}{2}$ в выражение для площади:

$$S\left(\frac{a}{2}\right) = \frac{h \left(a \cdot \frac{a}{2} — \left(\frac{a}{2}\right)^2\right)}{a — b} = \frac{h\left(\frac{a^2}{2} — \frac{a^2}{4}\right)}{a — b} = \frac{h \cdot \frac{a^2}{4}}{a — b} = \frac{a^2h}{4(a — b)}$$

Случай 2: $\frac{a}{2} > b$

В этом случае наибольшая возможная длина $x$ — это $b$, и площадь:

$$S = b \cdot \frac{(a — b)h}{a — b} = bh$$

Шаг 8. Итоговая формула

$$\boxed{ S_{\text{max}} = \begin{cases} \displaystyle \frac{a^2h}{4(a — b)}, & \text{если } \frac{a}{2} \leq b \\ bh, & \text{если } \frac{a}{2} > b \end{cases} }$$

Шаг 9. Примеры

Пример а: $a = 80$, $b = 60$, $h = 100$

$$\frac{a}{2} = 40 < b = 60 \quad \Rightarrow \quad x = \frac{a}{2} \text{ допустимо}$$ $$S_{\text{max}} = bh = 60 \cdot 100 = 6000$$

Пример б: $a = 24$, $b = 8$, $h = 12$

$$\frac{a}{2} = 12 > b = 8 \quad \Rightarrow \quad x = \frac{a}{2} \text{ недопустимо}$$ $$S_{\text{max}} = \frac{24^2 \cdot 12}{4(24 — 8)} = \frac{576 \cdot 12}{64} = \frac{6912}{64} = 108$$

Ответ:

а) 6000
б) 108