ГДЗ 10-11 Класс Номер 32.38 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

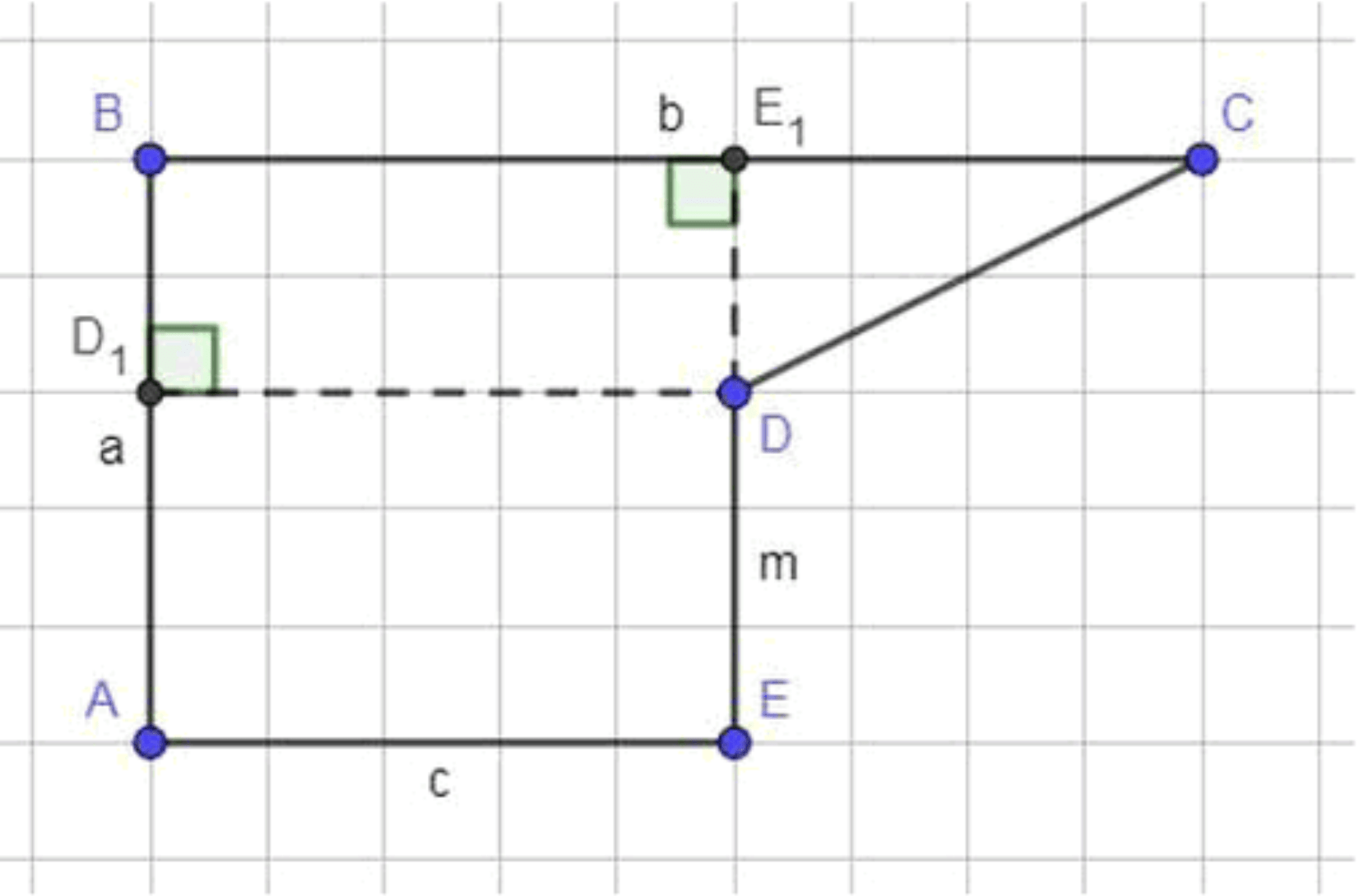
У пятиугольника ABCDE углы А, В и Е — прямые, АВ = а, ВС = Ь, АЕ = с, DE = m.

Впишите в пятиугольник прямоугольник наибольшей площади и вычислите эту площадь, если:

а) а = 7, b = 9, с = 3, m = 5;

б) а = 7, b = 18, с = 3, m = 1.

Отобразим условие задачи:

Дано: пятиугольник $ABCDE$; $\angle A = \angle B = \angle E = 90^\circ$; $AB = a$; $BC = b$; $AE = c$; $DE = m$;

Найти: прямоугольник с наибольшей площадью;

Решение:

Опустим перпендикуляры $DE_1$ на сторону $BC$ и $DD_1$ на сторону $AB$;

Наибольшую площадь имеет либо прямоугольник $ABE_1E$, либо прямоугольник, вписанный в прямоугольную трапецию $BD_1DC$;

Площадь прямоугольника $ABE_1E$ равна:

$$S_{ABE_1E} = AB \cdot BE = a \cdot c;$$

Площадь трапеции $BD_1DC$ равна:

$$S_{BD_1DC} = \frac{1}{2} DE_1 \cdot (BC + DD_1) = \frac{1}{2}(AB — DE)(BC + AE) = \frac{1}{2}(a — m)(b + c);$$

Во втором случае используем формулу, полученную в задаче 32.37:

$$s\left(\frac{b}{2}\right) = \frac{b^2 \cdot (a — m)}{4b — 4c};$$

а) Если $a = 7$, $b = 9$, $c = 3$ и $m = 5$:

$$S_{ABE_1E} = 7 \cdot 3 = 21;$$ $$S_{BD_1DC} = \frac{1}{2}(7 — 5)(9 + 3) = \frac{1}{2} \cdot 2 \cdot 12 = 12;$$

$S_{ABE_1E} > S_{BD_1DC}$, значит:

$$S_{max} = S_{ABE_1E} = 21;$$

б) Если $a = 7$, $b = 18$, $c = 3$ и $m = 1$:

$$S_{ABE_1E} = 7 \cdot 3 = 21;$$ $$S_{BD_1DC} = \frac{1}{2}(7 — 1)(18 + 3) = \frac{1}{2} \cdot 6 \cdot 21 = 63;$$

$S_{BD_1DC} > S_{ABE_1E}$ и $\frac{b}{2} = \frac{18}{2} = 9 > c$, значит:

$$S_{max} = \frac{18^2 \cdot (7 — 1)}{4 \cdot 18 — 4 \cdot 3} = \frac{324 \cdot 6}{72 — 12} = \frac{1944}{60} = 32{,}4;$$

Ответ: а) 21; б) 32,4.

Дано:

• $ABCDE$ — пятиугольник,
• $\angle A = \angle B = \angle E = 90^\circ$,
• $AB = a$, $BC = b$, $AE = c$, $DE = m$.

Найти:

• Прямоугольник с наибольшей площадью, вписанный в пятиугольник.

Решение:

Шаг 1. Анализ фигуры

Пятиугольник $ABCDE$ имеет три прямых угла:

• $\angle A = 90^\circ$,
• $\angle B = 90^\circ$,
• $\angle E = 90^\circ$.

Это даёт следующую геометрию:

• Отрезки $AB$ и $AE$ перпендикулярны: $AB$ вертикальный, $AE$ горизонтальный.
• $AB$ и $BC$ образуют прямой угол в точке $B$, значит $BC$ горизонтален.
• $AE$ и $DE$ соединяются под прямым углом в $E$, значит $DE$ вертикален.

Итоговая фигура выглядит как прямой угол в точке $A$, с вырезом в правой части (участок $D$), и представляет собой замкнутую выпуклую фигуру.

Шаг 2. Построим перпендикуляры

1. Опустим перпендикуляр $DE_1$ из точки $D$ на сторону $BC$.
2. Опустим перпендикуляр $DD_1$ из точки $D$ на сторону $AB$.

Это позволяет:

• Разделить фигуру на прямоугольник $ABE_1E$ и трапецию $BD_1DC$.
• Рассмотреть два возможных вписанных прямоугольника:
  • Первый — в левом прямоугольнике $ABE_1E$.
  • Второй — в трапеции $BD_1DC$.

Шаг 3. Первый случай: прямоугольник $ABE_1E$

Это прямоугольник с вершинами:

• $A$ и $B$ — на вертикальной и горизонтальной сторонах;
• $E$ и $E_1$ — на продолжении сторон.

Стороны:

• $AB = a$ (вертикаль),
• $BE = c$ (горизонталь, равна длине $AE$).

Тогда:

$$S_{ABE_1E} = AB \cdot BE = a \cdot c.$$

Шаг 4. Второй случай: прямоугольник, вписанный в трапецию $BD_1DC$

Трапеция образована точками:

• $B$, $D_1$, $D$, $C$.

Геометрия:

• Основания: $BC = b$, $D_1D = DD_1 = a — m$,
• Высота: $DE_1 = AE + BC = c + b$.

Площадь трапеции:

$$S_{\text{трапеции}} = \frac{1}{2} \cdot h \cdot (b + (a — m)) = \frac{1}{2}(a — m)(b + c).$$

Шаг 5. Используем результат из задачи 32.37

Для прямоугольника, вписанного в прямоугольную трапецию, с основаниями $b$ и $c$, и высотой $a — m$, формула максимальной площади имеет вид:

$$S = \frac{b^2 \cdot (a — m)}{4b — 4c}.$$

Это используется при условии, что:

$$\frac{b}{2} > c,$$

иначе прямоугольник не помещается целиком, и нужно рассматривать всю трапецию.

Шаг 6. Подстановка значений:

а) Если $a = 7$, $b = 9$, $c = 3$, $m = 5$

Вычислим площадь прямоугольника $ABE_1E$:

$$S_{ABE_1E} = 7 \cdot 3 = 21.$$

Площадь трапеции:

$$S_{BD_1DC} = \frac{1}{2}(7 — 5)(9 + 3) = \frac{1}{2} \cdot 2 \cdot 12 = 12.$$

Сравниваем:

$$21 > 12,$$

значит максимальная площадь:

$$S_{max} = S_{ABE_1E} = 21.$$

б) Если $a = 7$, $b = 18$, $c = 3$, $m = 1$

Площадь прямоугольника $ABE_1E$:

$$S_{ABE_1E} = 7 \cdot 3 = 21.$$

Площадь трапеции:

$$S_{BD_1DC} = \frac{1}{2}(7 — 1)(18 + 3) = \frac{1}{2} \cdot 6 \cdot 21 = 63.$$

Сравниваем:

$$63 > 21.$$

Теперь проверим, можно ли применить формулу из задачи 32.37:

$$\frac{b}{2} = \frac{18}{2} = 9 > c = 3.$$

Условие выполнено, можно применить формулу:

$$S = \frac{b^2 \cdot (a — m)}{4b — 4c} = \frac{18^2 \cdot (7 — 1)}{4 \cdot 18 — 4 \cdot 3} = \frac{324 \cdot 6}{72 — 12} = \frac{1944}{60} = 32.4.$$

Это и будет наибольшая возможная площадь прямоугольника в данном случае.

Ответ:

а) 21
б) 32,4