ГДЗ 10-11 Класс Номер 32.40 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

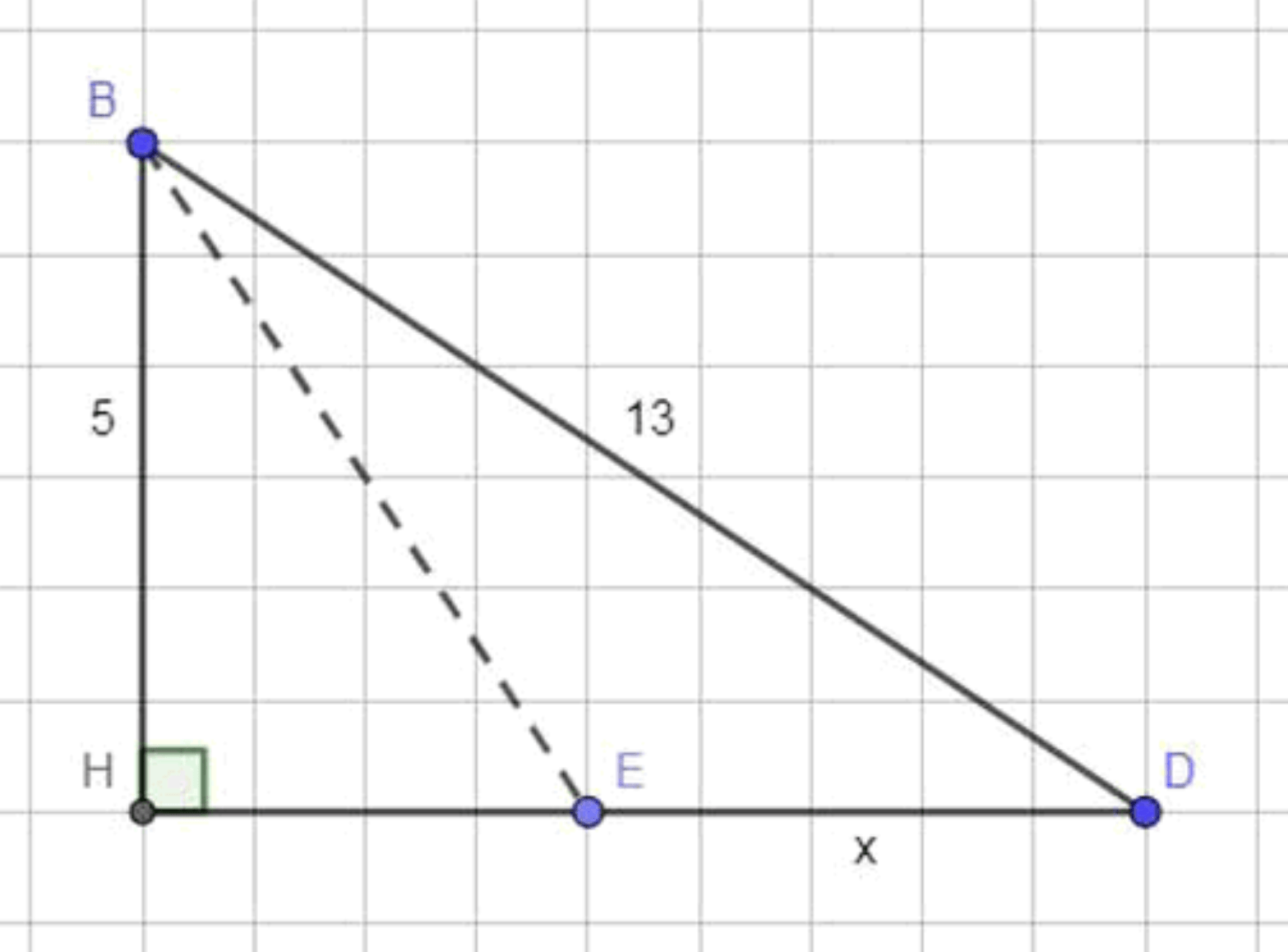
База находится в лесу в 5 км от дороги, а в 13 км от базы на этой дороге есть железнодорожная станция. Пешеход по дороге идёт со скоростью 5 км/ч, а по лесу— 3 км/ч. За какое минимальное время пешеход может добраться от базы до станции?

Отобразим условие задачи:

Пусть точка $B$ — база, точка $D$ — станция и прямая $DH$ — дорога, где точка $H$ — основание перпендикуляра, опущенного из точки $B$;
$BH=5\text{ км},BD=13\text{ км}$

$$DH=\sqrt{B{D}^2-B{H}^2}=\sqrt{{13}^2-5^2}=\sqrt{169-25}=\sqrt{144}=12\text{ км}$$

Пусть пешеход вышел на дорогу в точке $E$, и $ED=x$. Тогда:

$$HE=DH-ED=12-x$$$$BE=\sqrt{B{H}^2+H{E}^2}=\sqrt{5^2+(12-x{)}^2}=\sqrt{169-24x+x^2}$$

Время, затраченное пешеходом на весь путь:

$$t(x)=\frac{ED}{v_1}+\frac{BE}{v_2}=\frac{x}{5}+\frac{\sqrt{169-24x+x^2}}{3}$$$$v_1=5\text{ км/ч}\text{(по дороге)},v_2=3\text{ км/ч}\text{(по лесу)}$$

Производная функции:

$$t^{\mathrm{\prime }}(x)=\frac{d}{dx}(\frac{x}{5}+\frac{\sqrt{169-24x+x^2}}{3})$$$$t^{\mathrm{\prime }}(x)=\frac{1}{5}+\frac{1}{3}\cdot \frac{(169-24x+x^2{)}^{\mathrm{\prime }}}{2\sqrt{169-24x+x^2}}=\frac{1}{5}+\frac{2x-24}{6\sqrt{169-24x+x^2}}$$$$t^{\mathrm{\prime }}(x)=\frac{1}{5}+\frac{x-12}{3\sqrt{169-24x+x^2}}$$$$t^{\mathrm{\prime }}(x)=\frac{3\sqrt{169-24x+x^2}+5(x-12)}{15\sqrt{169-24x+x^2}}$$

(Используется формула производной сложной функции)

Промежуток возрастания:

$$3\sqrt{169-24x+x^2}+5(x-12)\ge 0$$$$3\sqrt{169-24x+x^2}\ge 5(12-x)$$

Возведём обе части в квадрат:

$$9(169-24x+x^2)\ge 25(144-24x+x^2)$$$$1521-216x+9x^2\ge 3600-600x+25x^2$$$$16x^2-384x+2079\le 0$$$$D={384}^2-4\cdot 16\cdot 2079=147456-133056=14400={120}^2$$$$x_1=\frac{384-120}{2\cdot 16}=\frac{264}{32}=\frac{33}{4},x_2=\frac{384+120}{2\cdot 16}=\frac{504}{32}=\frac{63}{4}$$$$(x-\frac{33}{4})(x-\frac{63}{4})\ge 0\Rightarrow \frac{33}{4}\le x\le \frac{63}{4}$$

Наименьшее значение:

$$t\left(\frac{33}{4}\right)=\frac{33}{20}+\frac{\sqrt{169-24\cdot \frac{33}{4}+{\left(\frac{33}{4}\right)}^2}}{3}$$$$=\frac{33}{20}+\frac{\sqrt{169-198+\frac{1089}{16}}}{3}=\frac{33}{20}+\frac{\sqrt{\frac{625}{16}}}{3}=\frac{33}{20}+\frac{25}{12}=\frac{99+125}{60}=\frac{224}{60}=3\frac{44}{60}\text{ ч}$$

Ответ: $3$ часа $44$ минуты.

Условие задачи

• База находится в лесу.
• Расстояние от базы до дороги (по перпендикуляру) — 5 км.
• На этой дороге в 13 км от базы (по прямой) расположена железнодорожная станция.
• Пешеход может идти:
  • по дороге со скоростью $v_1=5$ км/ч,
  • по лесу со скоростью $v_2=3$ км/ч.

Найти: минимальное время движения пешехода от базы до станции.

Шаг 1. Построим геометрическую модель

Обозначим:

• $B$ — база (в лесу),
• $D$ — железнодорожная станция (на дороге),
• $H$ — основание перпендикуляра из точки $B$ на дорогу,
• $E$ — точка выхода пешехода из леса на дорогу (где угодно между $H$ и $D$).

Известно:

• $BH=5$ км — расстояние от базы до дороги,
• $BD=13$ км — расстояние от базы до станции по прямой.

По теореме Пифагора найдём длину дороги между $H$ и $D$:

$$DH=\sqrt{B{D}^2-B{H}^2}=\sqrt{{13}^2-5^2}=\sqrt{169-25}=\sqrt{144}=12\text{ км}$$

Шаг 2. Обозначим переменную

Пусть пешеход выходит на дорогу в точке $E$, между $H$ и $D$. Обозначим:

• $x=ED$ — расстояние от точки выхода до станции вдоль дороги (измеряется по дороге).
• Тогда расстояние от $H$ до точки выхода $E$: $HE=12-x$.

Пешеход идёт:

• по лесу от $B$ до $E$ — диагональ прямоугольного треугольника с катетами $BH=5$ и $HE=12-x$,
• по дороге от $E$ до $D$, т.е. $ED=x$.

Шаг 3. Выразим длину пути по лесу

Длина отрезка $BE$:

$$BE=\sqrt{B{H}^2+H{E}^2}=\sqrt{5^2+(12-x{)}^2}=\sqrt{25+(144-24x+x^2)}=$$

$$=\sqrt{169-24x+x^2}$$

Шаг 4. Запишем функцию времени

Пешеход тратит:

• ${\displaystyle \frac{x}{5}}$ часов на участок дороги,
• ${\displaystyle \frac{\sqrt{169-24x+x^2}}{3}}$ часов на участок леса.

Функция полного времени:

$$t(x)=\frac{x}{5}+\frac{\sqrt{169-24x+x^2}}{3}$$

Ограничение: $0\le x\le 12$ — потому что $x$ — расстояние от точки выхода до станции вдоль дороги, а длина всей дороги между $H$ и $D$ — 12 км.

Шаг 5. Найдём производную функции

Найдём $t^{\mathrm{\prime }}(x)$:

$$t^{\mathrm{\prime }}(x)=\frac{1}{5}+\frac{1}{3}\cdot \frac{d}{dx}\left(\sqrt{169-24x+x^2}\right)$$

Для производной корня:

$$\frac{d}{dx}\left(\sqrt{f(x)}\right)=\frac{f^{\mathrm{\prime }}(x)}{2\sqrt{f(x)}}$$

Внутри корня $f(x)=x^2-24x+169$, производная:

$$f^{\mathrm{\prime }}(x)=2x-24$$

Тогда:

$$t^{\mathrm{\prime }}(x)=\frac{1}{5}+\frac{1}{3}\cdot \frac{2x-24}{2\sqrt{169-24x+x^2}}=\frac{1}{5}+\frac{x-12}{3\sqrt{169-24x+x^2}}$$

Шаг 6. Приравняем производную к нулю

$$t^{\mathrm{\prime }}(x)=0\Rightarrow \frac{1}{5}+\frac{x-12}{3\sqrt{169-24x+x^2}}=0$$

Умножим обе части на $3\sqrt{169-24x+x^2}$:

$$\frac{3\sqrt{169-24x+x^2}}{5}+x-12=0\Rightarrow 3\sqrt{169-24x+x^2}=5(12-x)$$

Шаг 7. Возведём обе части в квадрат

$$9(169-24x+x^2)=25(144-24x+x^2)$$

Раскроем скобки:

$$1521-216x+9x^2=3600-600x+25x^2$$

Перенесём всё в одну сторону:

$$1521-216x+9x^2-3600+600x-25x^2=0\Rightarrow -2079+384x-16x^2=0\Rightarrow$$

$$16x^2-384x+2079=0$$

Шаг 8. Решим квадратное уравнение

$$16x^2-384x+2079=0$$

Найдём дискриминант:

$$D={384}^2-4\cdot 16\cdot 2079=147456-133056=14400={120}^2$$

Найдём корни:

$$x=\frac{384\pm 120}{2\cdot 16}=\frac{504}{32}=\frac{63}{4},\frac{264}{32}=\frac{33}{4}$$

Точка минимума: так как $t(x)$ убывает до меньшего корня и возрастает после него, то минимум достигается в точке:

$$x=\frac{33}{4}=8.25\text{ км}$$

Шаг 9. Найдём минимальное время

Подставим $x=\frac{33}{4}$ в функцию:

$$t\left(\frac{33}{4}\right)=\frac{33}{20}+\frac{1}{3}\cdot \sqrt{169-24\cdot \frac{33}{4}+{\left(\frac{33}{4}\right)}^2}$$

Посчитаем подкоренное выражение:

$$24\cdot \frac{33}{4}=198,{\left(\frac{33}{4}\right)}^2=\frac{1089}{16}$$$$169-198+\frac{1089}{16}=-29+\frac{1089}{16}=\frac{-464+1089}{16}=\frac{625}{16}$$$$\sqrt{\frac{625}{16}}=\frac{25}{4}$$

Теперь время:

$$t=\frac{33}{20}+\frac{1}{3}\cdot \frac{25}{4}=\frac{33}{20}+\frac{25}{12}$$

Приводим к общему знаменателю (LCM 60):

$$\frac{33}{20}=\frac{99}{60},\frac{25}{12}=\frac{125}{60}\Rightarrow t=\frac{99+125}{60}=\frac{224}{60}=3\frac{44}{60}$$

Ответ:

$$\boxed{{\displaystyle 3\text{ часа }44\text{ минуты}}}$$