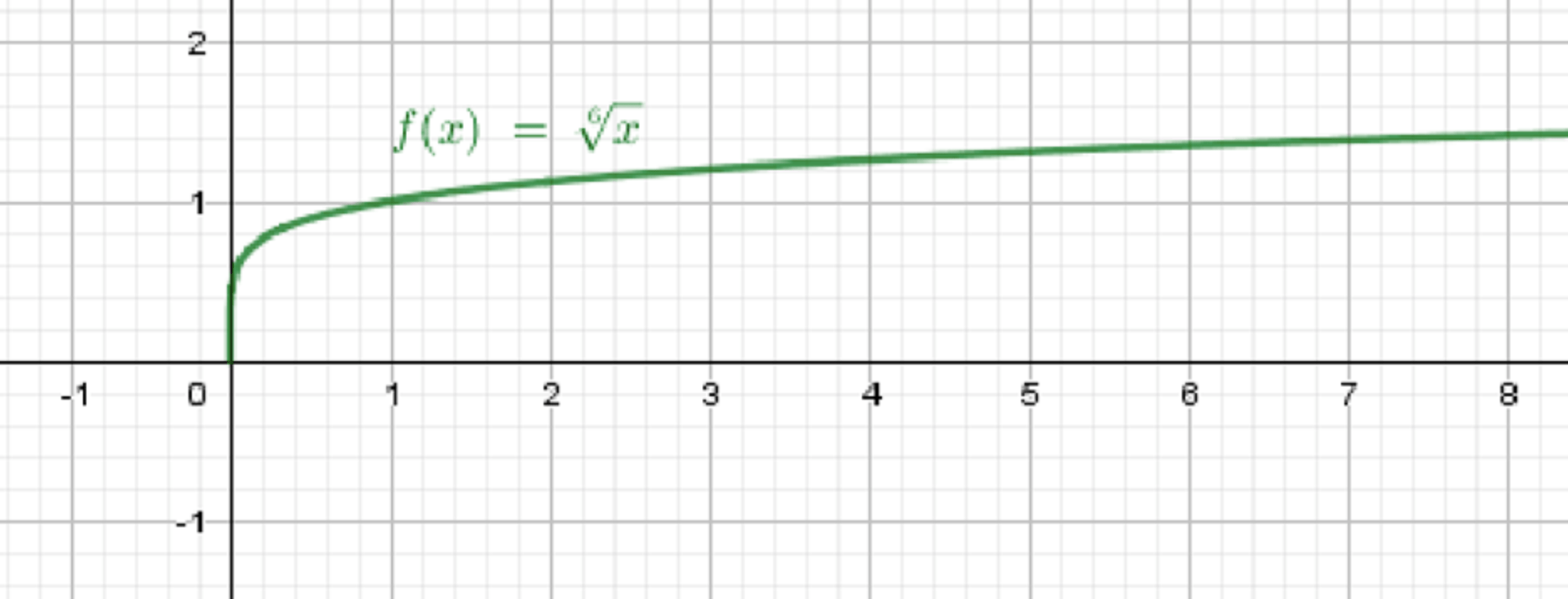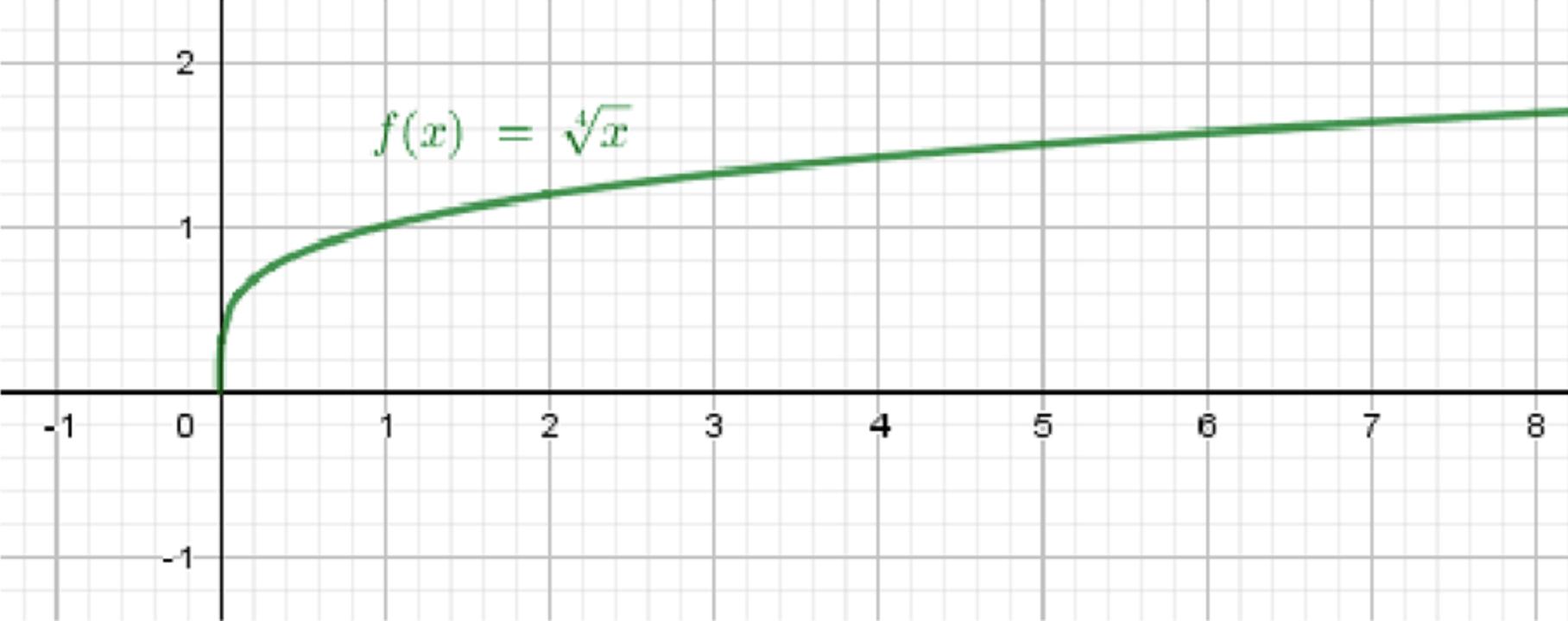ГДЗ 10-11 Класс Номер 34.1 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y = \sqrt[3]{x}$

б) $y = \sqrt[6]{x}$

в) $y = \sqrt[4]{x}$

г) $y=\sqrt[5]{x}$

Построить график функции:

а) $y = \sqrt[3]{x}$

Область определения функции:
$D(y) = (-\infty; +\infty)$

Функция является нечетной:
$y(-x) = \sqrt[3]{-x} = -\sqrt[3]{x} = -y(x)$

Координаты некоторых точек:

График функции:

б) $y = \sqrt[6]{x}$

Область определения функции:
$D(y) = [0; +\infty)$

Координаты некоторых точек:

График функции:

в) $y = \sqrt[4]{x}$

Область определения функции:
$D(y) = [0; +\infty)$

Координаты некоторых точек:

График функции:

г) $y = \sqrt[5]{x}$

Область определения функции:
$D(y) = (-\infty; +\infty)$

Функция является нечетной:
$y(-x) = \sqrt[5]{-x} = -\sqrt[5]{x} = -y(x)$

Координаты некоторых точек:

График функции:

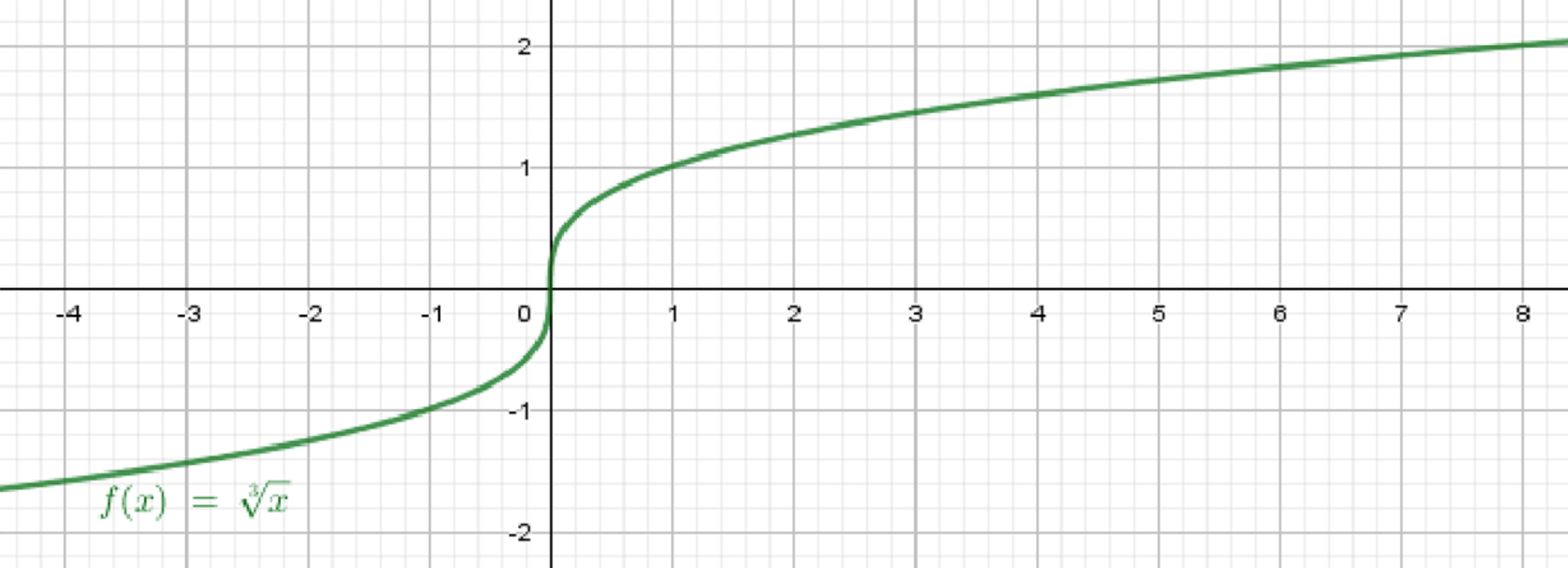
а) $y = \sqrt[3]{x}$

1. Область определения
Корень нечетной степени извлекается из любого действительного числа.
Значит:

$$D(y) = (-\infty; +\infty)$$

2. Четность функции
Проверим, как ведет себя функция при замене $x \to -x$:

$$y(-x) = \sqrt[3]{-x} = -\sqrt[3]{x} = -y(x)$$

Следовательно, функция нечётная — её график симметричен относительно начала координат.

3. Таблица значений

4. Поведение графика

• Проходит через точку $(0, 0)$;
• При $x > 0$, $y$ медленно возрастает;
• При $x < 0$, $y$ убывает, отрицательное;
• График плавно пересекает ось абсцисс и ось ординат в начале координат.

б) $y = \sqrt[6]{x}$

1. Область определения
Корень чётной степени (6) извлекается только из неотрицательных чисел, т.е. $x \geq 0$

$$D(y) = [0; +\infty)$$

2. Четность
Функция определена только для $x \geq 0$, значит вопрос о чётности не имеет смысла.

3. Таблица значений

4. Поведение графика

• График начинается в точке $(0, 0)$;
• Значения функции растут очень медленно при увеличении $x$;
• График лежит в первой четверти, монотонно возрастает.

в) $y = \sqrt[4]{x}$

1. Область определения
Корень четной степени (4) также извлекается только из неотрицательных чисел:

$$D(y) = [0; +\infty)$$

2. Четность
Как и предыдущая, функция определена только при $x \geq 0$, нечётность/чётность не рассматриваются.

3. Таблица значений

4. Поведение графика

• Начинается в точке $(0, 0)$;
• Растёт медленно, особенно при больших значениях $x$;
• График лежит в первой четверти, как и в случае с $y = \sqrt[6]{x}$, но растёт быстрее.

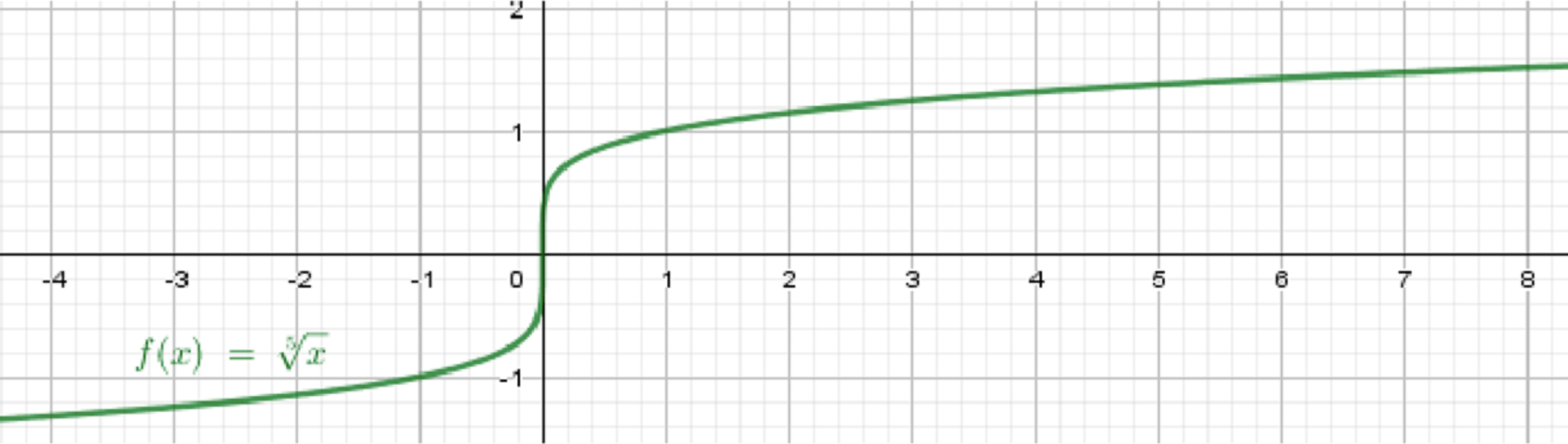
г) $y = \sqrt[5]{x}$

1. Область определения
Поскольку степень корня нечетная, функция определена на всей числовой прямой:

$$D(y) = (-\infty; +\infty)$$

2. Четность функции

$$y(-x) = \sqrt[5]{-x} = -\sqrt[5]{x} = -y(x) \Rightarrow \text{Функция нечётная}$$

3. Таблица значений

4. Поведение графика

• Проходит через начало координат $(0, 0)$;
• График симметричен относительно начала координат;
• Убывает при $x < 0$, возрастает при $x > 0$;
• Рост и убывание — медленные, но быстрее, чем у $\sqrt[6]{x}$.