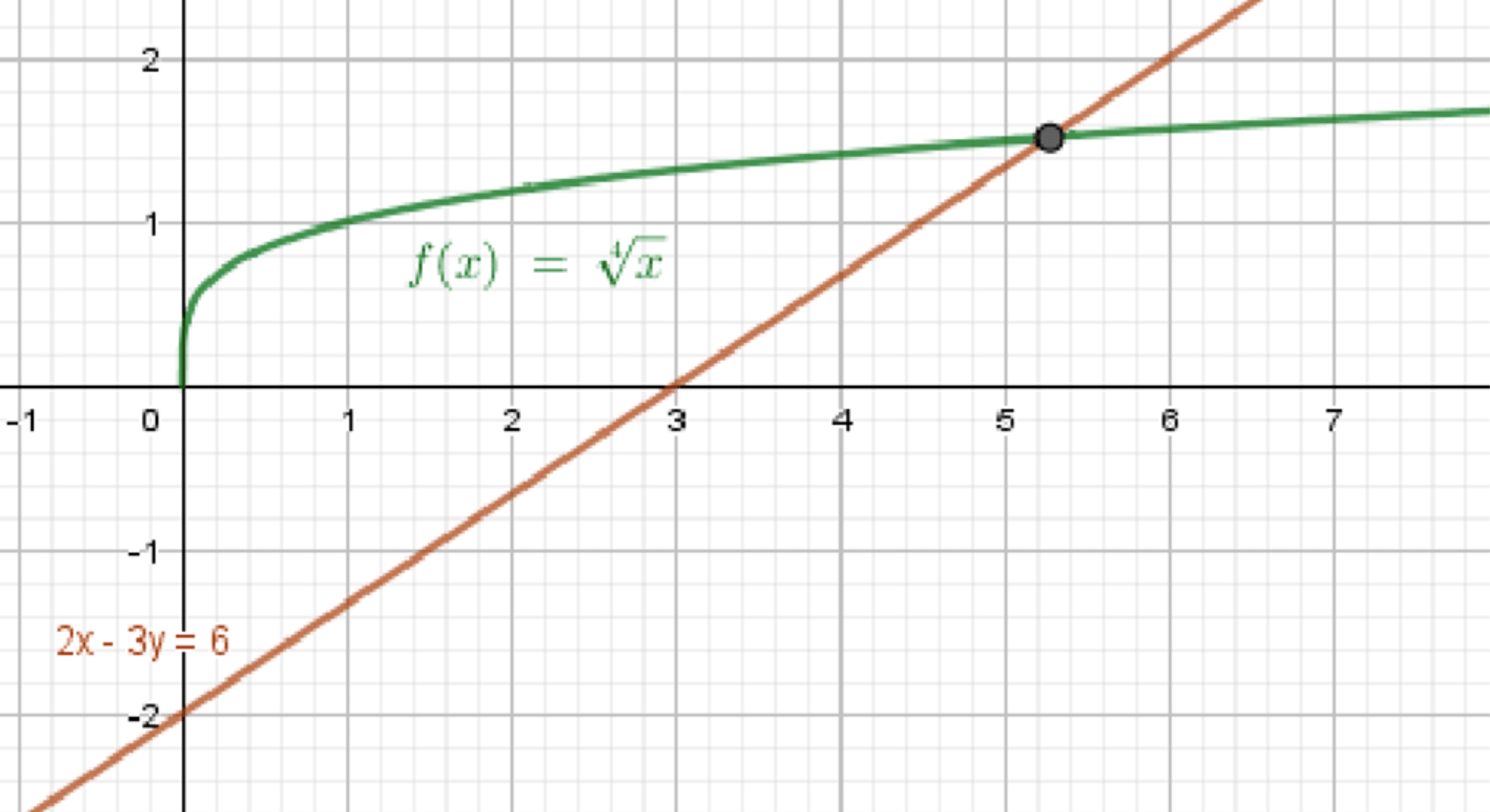ГДЗ 10-11 Класс Номер 34.10 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Определите число решений системы уравнений:

а)

$$\{\begin{array}{l}y=\sqrt[4]{x}\\ 2x-3y=6\end{array}$$

б)

$$\{\begin{array}{l}y=\sqrt[3]{x}\\ 3y-4x=0\end{array}$$

в)

$$\{\begin{array}{l}y=\sqrt[3]{x}\\ 6-2x-3y=0\end{array}$$

г)

$$\{\begin{array}{l}y=\sqrt{x}\\ 5+x-2y=0\end{array}$$

Определить число решений системы уравнений:

а)

$$\begin{cases} y = \sqrt[4]{x} \\ 2x — 3y = 6 \end{cases}$$

Второе уравнение:
$2x — 3y = 6;$
$3y = 2x — 6;$
$y = \frac{2}{3}x — 2;$

$$\begin{array}{|c|c|c|} \hline x & 0 & 3 \\ \hline y & -2 & 0 \\ \hline \end{array}$$

Графики функций:

Ответ: 1 решение.

б)

$$\begin{cases} y = \sqrt[3]{x} \\ 3y — 4x = 0 \end{cases}$$

Второе уравнение:
$3y — 4x = 0;$
$3y = 4x;$
$y = \frac{4}{3}x;$

$$\begin{array}{|c|c|c|} \hline x & 0 & 3 \\ \hline y & 0 & 4 \\ \hline \end{array}$$

Графики функций:

Ответ: 3 решения.

в)

$$\begin{cases} y = \sqrt[3]{x} \\ 6 — 2x — 3y = 0 \end{cases}$$

Второе уравнение:
$6 — 2x — 3y = 0;$
$3y = 6 — 2x;$
$y = 2 — \frac{2}{3}x;$

$$\begin{array}{|c|c|c|} \hline x & 0 & 3 \\ \hline y & 2 & 0 \\ \hline \end{array}$$

Графики функций:

Ответ: 1 решение.

г)

$$\begin{cases} y = \sqrt{x} \\ 5 + x — 2y = 0 \end{cases}$$

Второе уравнение:
$5 + x — 2y = 0;$
$2y = x + 5;$
$y = \frac{1}{2}x + \frac{5}{2};$

$$\begin{array}{|c|c|c|} \hline x & -1 & 3 \\ \hline y & 2 & 4 \\ \hline \end{array}$$

Графики функций:

Ответ: 0 решений.

а)

$$\begin{cases} y = \sqrt[4]{x} \\ 2x — 3y = 6 \end{cases}$$

Шаг 1: Анализ первого уравнения

$$y = \sqrt[4]{x}$$

• Это функция четвёртой коренной степени:

  $$y = x^{1/4}$$

• Область определения (ОДЗ):
  Корень чётной степени определён только при $x \geq 0$.
• Значения функции:
  $y \geq 0$, потому что корень четной степени не может быть отрицательным.
• График:
  — Монотонно возрастает
  — Начинается в точке (0, 0)
  — Идёт только в первой четверти (где $x \geq 0, y \geq 0$)

Шаг 2: Преобразуем второе уравнение

$$2x — 3y = 6 \Rightarrow 3y = 2x — 6 \Rightarrow y = \frac{2}{3}x — 2$$

• Это уравнение прямой в виде $y = kx + b$, где:
  • Угол наклона $k = \frac{2}{3}$ — положительный: прямая поднимается вправо вверх
  • Смещение по y: $b = -2$ — прямая проходит через точку (0, -2)
• Область определения: вся числовая прямая (можно подставлять любые значения $x$)
• Прямая проходит в двух четвертях:
  — При $x < 3$, $y < 0$
  — При $x > 3$, $y > 0$

Шаг 3: Решаем графически

• Функция $y = \sqrt[4]{x}$ существует только при $x \geq 0$ и $y \geq 0$
• Прямая $y = \frac{2}{3}x — 2$ принимает положительные значения $y$, начиная с точки $x = 3$
• Проверим:
  Подставим $x = 3$ в прямую:

  $$y = \frac{2}{3} \cdot 3 — 2 = 2 — 2 = 0$$

  Значит, в точке $x = 3$ обе функции принимают $y = 0$

• Это и есть точка пересечения в допустимой области — (3, 0)

Ответ: 1 решение

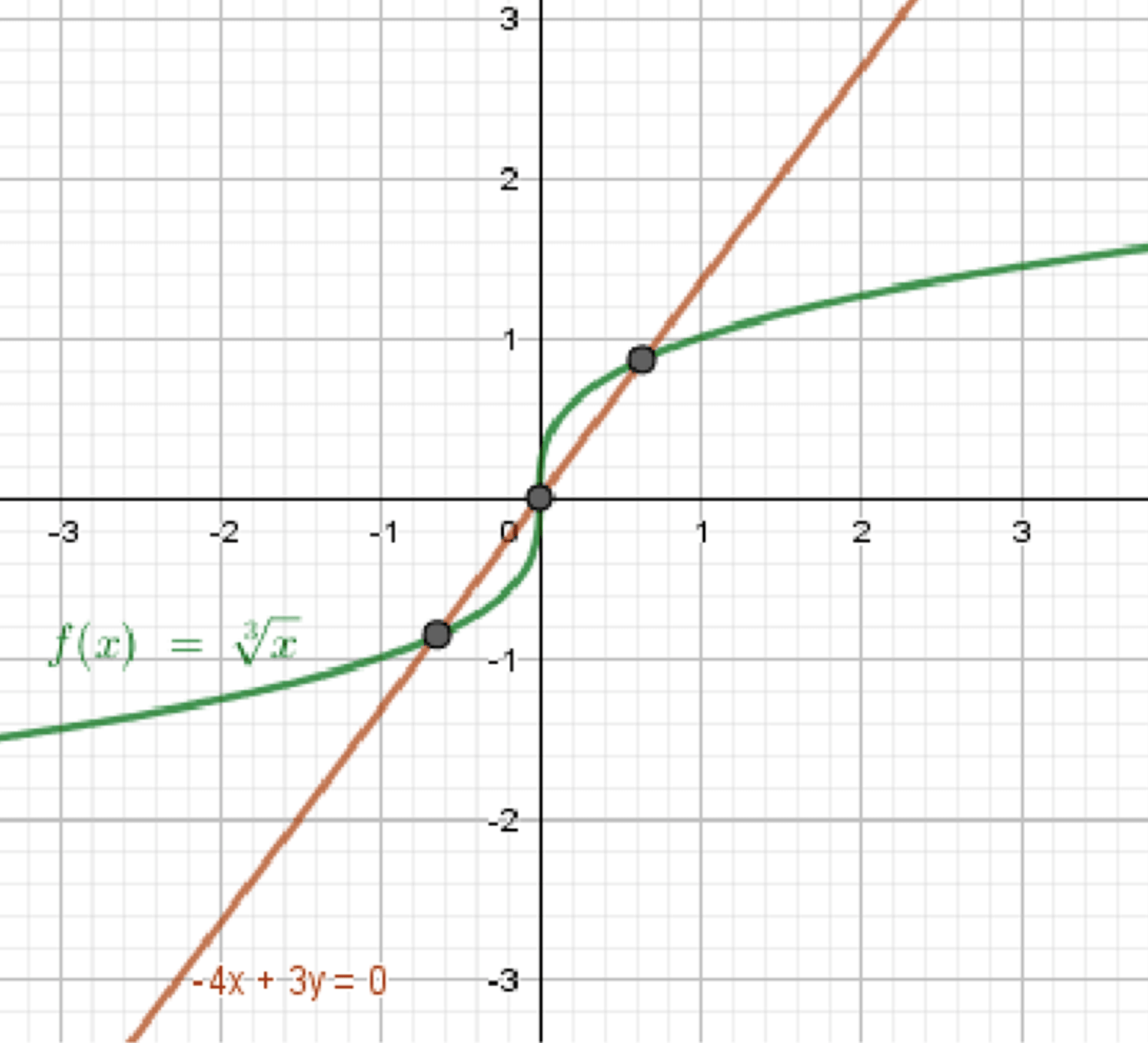
б)

$$\begin{cases} y = \sqrt[3]{x} \\ 3y — 4x = 0 \end{cases}$$

Шаг 1: Первый график

$$y = \sqrt[3]{x} = x^{1/3}$$

• Кубический корень определён при любом $x$, в отличие от чётного корня
• Значения $y$ могут быть и положительные, и отрицательные
  Примеры:
  • $x = -8 \Rightarrow y = -2$
  • $x = 0 \Rightarrow y = 0$
  • $x = 8 \Rightarrow y = 2$
• График:
  • Проходит через начало координат (0, 0)
  • Симметричен относительно начала координат
  • Монотонно возрастает
  • Идёт через все четыре четверти, но только вдоль прямой формы

Шаг 2: Второе уравнение

$$3y — 4x = 0 \Rightarrow y = \frac{4}{3}x$$

• Прямая с положительным наклоном $k = \frac{4}{3}$
• Проходит через начало координат
• Прямая восходит вправо, опускается влево — тоже через все четыре четверти

Шаг 3: Ищем пересечения

Решим уравнение системы:

$$y = \sqrt[3]{x}, \quad y = \frac{4}{3}x$$

Приравняем:

$$\sqrt[3]{x} = \frac{4}{3}x$$

Пусть $x = 0$:

• $\sqrt[3]{0} = 0$, $\frac{4}{3} \cdot 0 = 0$ → подходит

Пусть $x = 1$:

• $\sqrt[3]{1} = 1$, $\frac{4}{3} \cdot 1 = \frac{4}{3} \ne 1$

Найдём все решения уравнения:

$$x^{1/3} = \frac{4}{3}x \Rightarrow x^{1/3} — \frac{4}{3}x = 0 \Rightarrow x^{1/3} \left(1 — \frac{4}{3}x^{2/3} \right) = 0$$

Разберём по множителям:

• Первый множитель:

  $$x^{1/3} = 0 \Rightarrow x = 0$$

• Второй множитель:

  $$1 — \frac{4}{3}x^{2/3} = 0 \Rightarrow \frac{4}{3}x^{2/3} = 1 \Rightarrow x^{2/3} = \frac{3}{4} \Rightarrow x^2 = \left(\frac{3}{4}\right)^3 = \frac{27}{64} \Rightarrow x = \pm \sqrt{\frac{27}{64}} = \pm \frac{3\sqrt{3}}{8}$$

• Таким образом, 3 значения x:
  • $x = 0$
  • $x = +\frac{3\sqrt{3}}{8}$
  • $x = -\frac{3\sqrt{3}}{8}$
• У всех них найдутся соответствующие $y$

Ответ: 3 решения

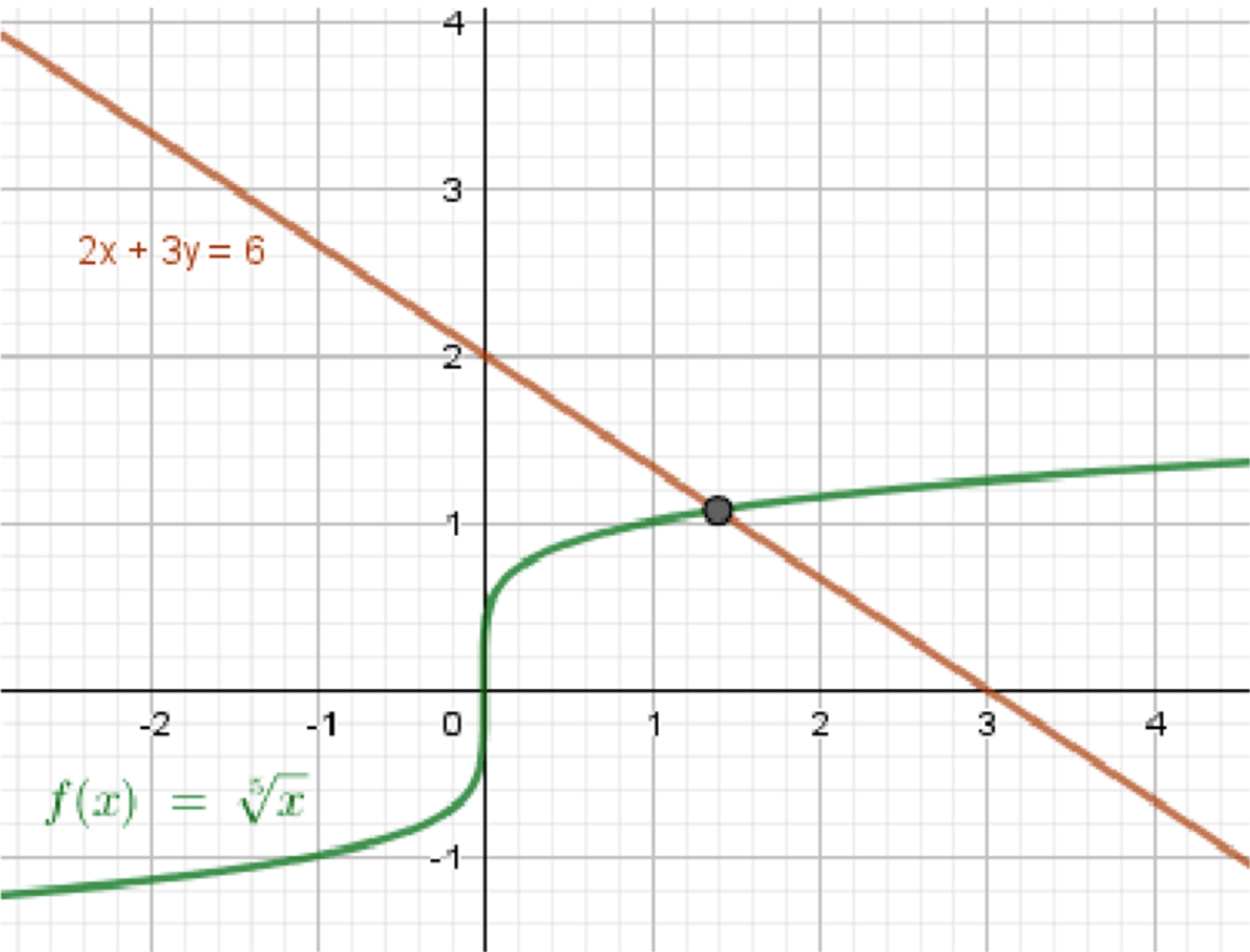
в)

$$\begin{cases} y = \sqrt[3]{x} \\ 6 — 2x — 3y = 0 \end{cases}$$

Шаг 1: Первый график

$y = \sqrt[3]{x}$ — уже разобрали в пункте б

• Область определения: вся числовая ось
• Значения: любые $y$
• Проходит через (0, 0)

Шаг 2: Второе уравнение

$$6 — 2x — 3y = 0 \Rightarrow 3y = 6 — 2x \Rightarrow y = 2 — \frac{2}{3}x$$

• Прямая с отрицательным наклоном $k = -\frac{2}{3}$
• Смещение по y: $b = 2$ → пересекает ось y в точке (0, 2)
• Проходит сверху-вниз (слева направо)

Шаг 3: Решим систему

Подставим:

$$\sqrt[3]{x} = 2 — \frac{2}{3}x$$

Решим:

$$x^{1/3} = 2 — \frac{2}{3}x \Rightarrow x^{1/3} + \frac{2}{3}x = 2$$

Это сложное уравнение, но видно, что при $x = 3$:

• $\sqrt[3]{3} \approx 1.44$
• $\frac{2}{3} \cdot 3 = 2$
• Левая часть: $1.44 + 2 = 3.44 \ne 2$ — не подходит

Проверим $x = 0$:

• $\sqrt[3]{0} = 0$
• $\frac{2}{3} \cdot 0 = 0$
• Левая часть: 0 → не подходит

Попробуем аналитически:

$$x^{1/3} = 2 — \frac{2}{3}x \Rightarrow x^{1/3} + \frac{2}{3}x — 2 = 0$$

Подставим $x = 3$:

• $\sqrt[3]{3} + 2 — 2 = \sqrt[3]{3} \ne 0$

Методом подбора или численно видно, что одно пересечение происходит в районе $x = 3$
Графически:

• $y = \sqrt[3]{x}$ растёт
• $y = 2 — \frac{2}{3}x$ убывает
  → Могут пересечься только в одной точке

Ответ: 1 решение

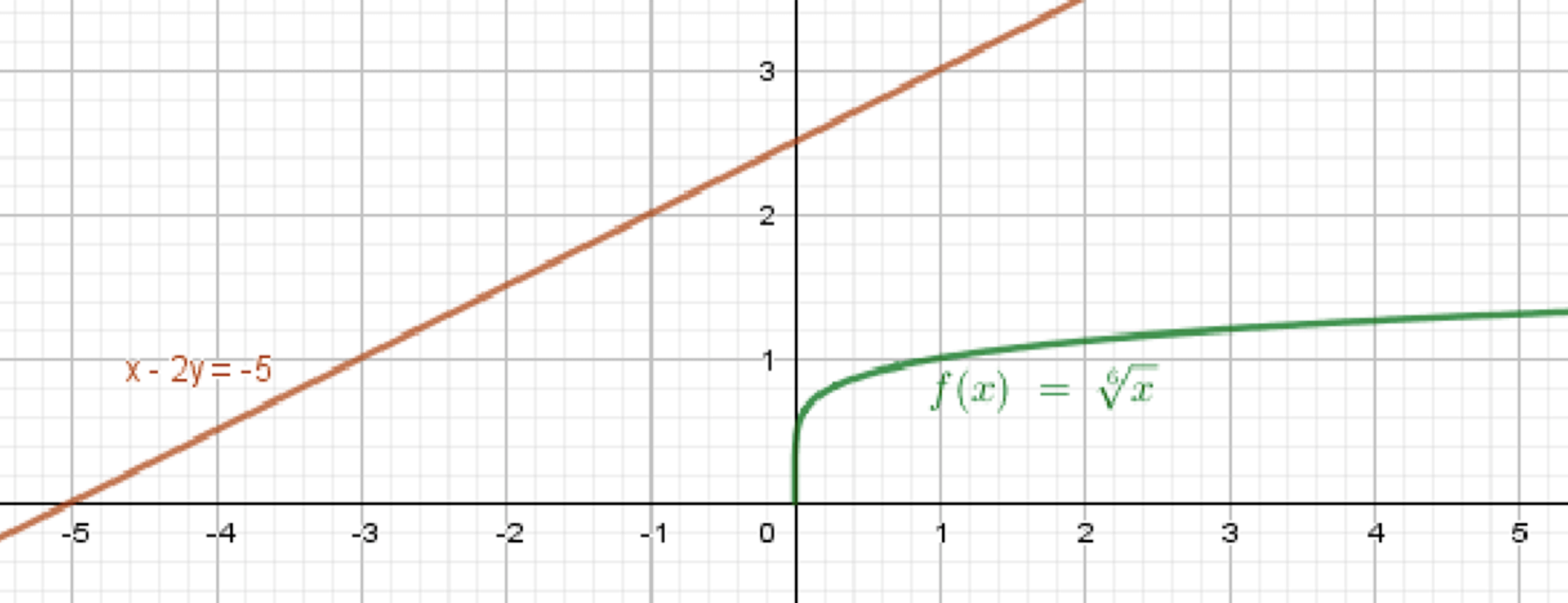
г)

$$\begin{cases} y = \sqrt{x} \\ 5 + x — 2y = 0 \end{cases}$$

Шаг 1: Первый график

$$y = \sqrt{x}$$

• Область определения: $x \geq 0$
• Значения: $y \geq 0$
• График:
  • Начинается в точке (0, 0)
  • Растёт, но убывающе замедляется
  • Только в первой четверти

Шаг 2: Второе уравнение

$$5 + x — 2y = 0 \Rightarrow 2y = x + 5 \Rightarrow y = \frac{1}{2}x + \frac{5}{2}$$

• Прямая с положительным наклоном
• Смещение по y: $\frac{5}{2}$
• Значит:
  • Когда $x = 0$, $y = 2.5$
  • Когда $x = -1$, $y = 2$

Шаг 3: Область пересечения

Сравним:

• $\sqrt{x}$ определена только при $x \geq 0$, $y \geq 0$
• Прямая начинается выше, чем кривая $\sqrt{x}$
  • Например: при $x = 0$, $\sqrt{0} = 0$, но по прямой $y = 2.5$
  • При $x = 3$:
    $\sqrt{3} \approx 1.73$,
    Прямая: $y = \frac{1}{2} \cdot 3 + \frac{5}{2} = 1.5 + 2.5 = 4$
• Прямая всё время выше параболы $y = \sqrt{x}$
  → Они не пересекаются

Ответ: 0 решений

Итоговые ответы:

а) 1 решение
б) 3 решения
в) 1 решение
г) 0 решений