ГДЗ 10-11 Класс Номер 34.11 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

а)

$$\{\begin{array}{l}y=\sqrt[4]{x}-1\\ y=x^2-2x-8\end{array}$$

б)

$$\{\begin{array}{l}y=2\sqrt[3]{x}\\ y=10x-16-x^2\end{array}$$

Определить число решений системы уравнений:

а)

$$\begin{cases} y = \sqrt[4]{x} — 1 \\ y = x^2 — 2x — 8 \end{cases}$$

$y = x^2 — 2x — 8$ — уравнение параболы:

$$x_0 = -\frac{b}{2a} = -\frac{-2}{2 \cdot 1} = \frac{2}{2} = 1;$$ $$y_0 = 1^2 — 2 \cdot 1 — 8 = 1 — 2 — 8 = -9;$$ $$\begin{array}{|c|c|c|c|} \hline x & 2 & 3 & 4 \\ \hline y & -8 & -5 & 0 \\ \hline \end{array}$$

Графики функций:

Ответ: 1 решение.

б)

$$\begin{cases} y = 2\sqrt[3]{x} \\ y = 10x — 16 — x^2 \end{cases}$$

$y = -x^2 + 10x — 16$ — уравнение параболы:

$$x_0 = -\frac{b}{2a} = -\frac{10}{2 \cdot (-1)} = \frac{10}{2} = 5;$$ $$y_0 = 10 \cdot 5 — 16 — 5^2 = 50 — 16 — 25 = 9;$$ $$\begin{array}{|c|c|c|c|} \hline x & 6 & 7 & 8 \\ \hline y & 8 & 5 & 0 \\ \hline \end{array}$$

Графики функций:

Ответ: 2 решения.

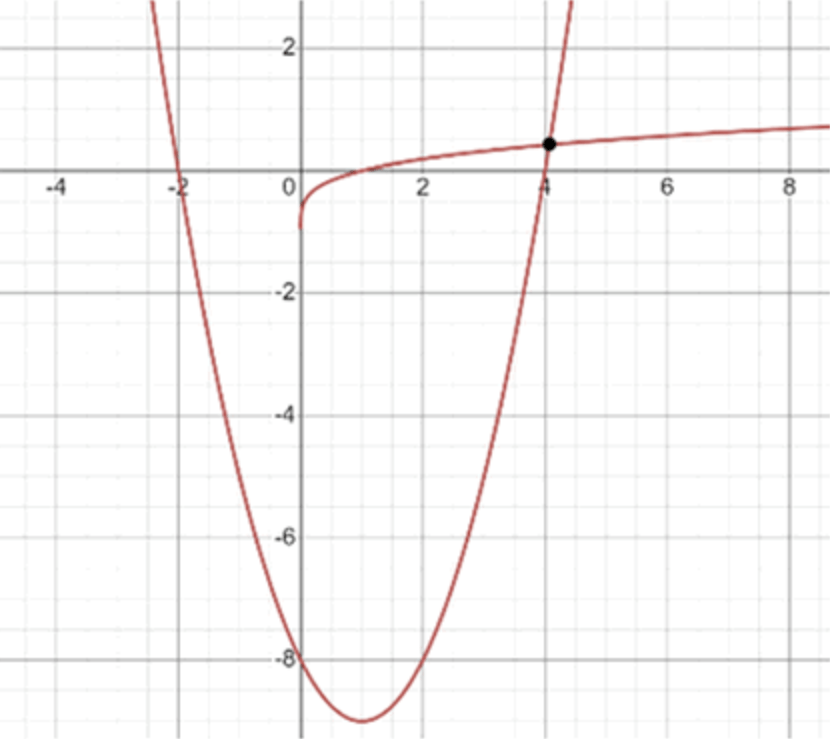
а)

$$\begin{cases} y = \sqrt[4]{x} — 1 \\ y = x^2 — 2x — 8 \end{cases}$$

Шаг 1: Анализ функции $y = \sqrt[4]{x} — 1$

• Это трансформированная корневая функция четвёртой степени:

  $$y = x^{1/4} — 1$$

• Область определения (ОДЗ):
  Корень четвёртой степени $x^{1/4}$ определён только при $x \geq 0$.
• Область значений:

  $$x^{1/4} \geq 0 \Rightarrow y = x^{1/4} — 1 \geq -1$$

• Характер графика:
  • Начинается с точки $(0, -1)$, т.к. $\sqrt[4]{0} = 0$
  • Монотонно возрастает
  • Идёт только в первой четверти, потому что $x \geq 0$, $y \geq -1$

Шаг 2: Анализ функции $y = x^2 — 2x — 8$

• Это парабола, открытая вверх, т.к. $a = 1 > 0$
• Координаты вершины параболы:

  $$x_0 = -\frac{b}{2a} = -\frac{-2}{2 \cdot 1} = 1$$ $$y_0 = 1^2 — 2 \cdot 1 — 8 = -9$$

  → Вершина: $(1, -9)$

• Форма и расположение графика:
  • Ветви вверх
  • Минимум в точке $(1, -9)$
  • Значения функции меньше 0 вблизи вершины, затем возрастают
• Таблица значений (дана):

  $$\begin{array}{|c|c|c|c|} \hline x & 2 & 3 & 4 \\ \hline y & -8 & -5 & 0 \\ \hline \end{array}$$

Шаг 3: Ищем точки пересечения — решаем систему

Ищем такие $x$, при которых:

$$\sqrt[4]{x} — 1 = x^2 — 2x — 8$$

Рассмотрим ОДЗ: $x \geq 0$, так как в первом уравнении есть корень четной степени.

Подставим несколько значений:

• $x = 0$:
  • Левая часть: $\sqrt[4]{0} — 1 = -1$
  • Правая часть: $0^2 — 2\cdot0 — 8 = -8$ → не совпадает
• $x = 4$:
  • Левая: $\sqrt[4]{4} — 1 = \sqrt[4]{4} \approx 1.414 — 1 = 0.414$
  • Правая: $16 — 8 — 8 = 0$ → не совпадает
• $x = 5$:
  • $\sqrt[4]{5} \approx 1.495$, $y \approx 0.495$
  • Правая: $25 — 10 — 8 = 7$ → больше

Значения пока не совпадают. Проверим, где графики могут пересекаться.

Геометрически:

• Первая функция возрастает от $-1$ вверх (медленно)
• Парабола убывает до $x = 1$, потом возрастает
• Следовательно, возможное пересечение — там, где парабола поднимается к нулю и выше, т.е. при $x > 3$

Подставим $x = 4$ (из таблицы):

• $y = \sqrt[4]{4} — 1 \approx 0.414$
• $y = 0$ по параболе → они близко

Между $x = 4$ и $x = 5$ прямая $y = \sqrt[4]{x} — 1$ возрастает
И парабола возрастает — графики пересекаются в одной точке

Вывод:

Графики пересекаются один раз при $x > 4$, где обе функции возрастают и имеют одно общее значение

Ответ: 1 решение

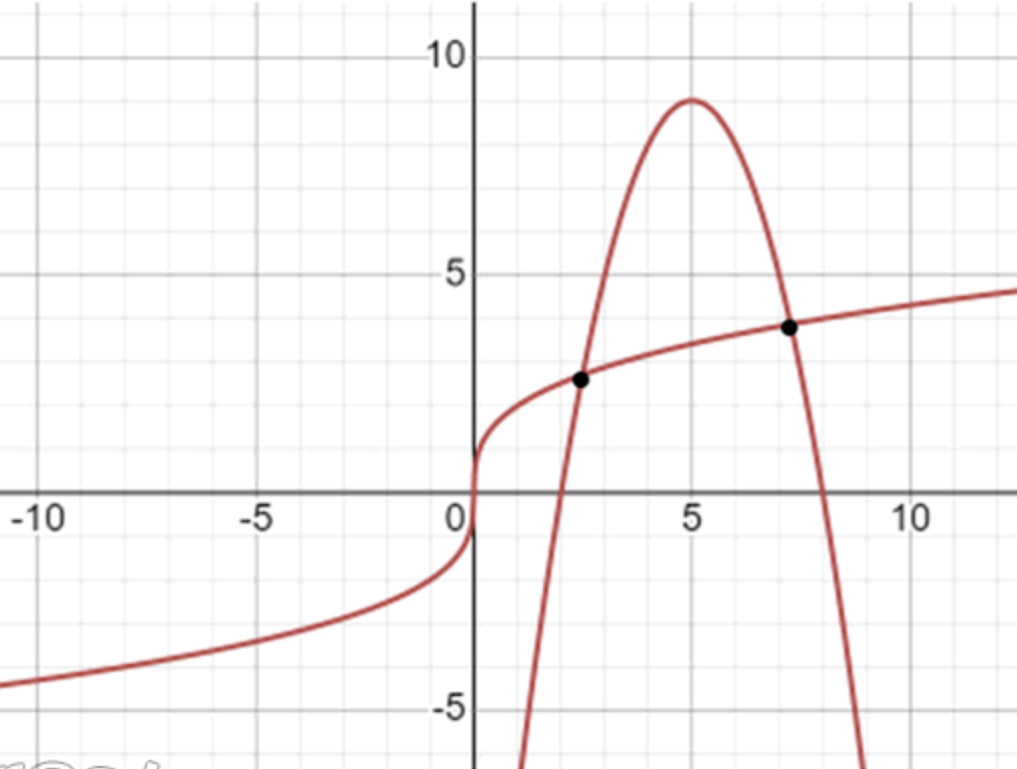
б)

$$\begin{cases} y = 2\sqrt[3]{x} \\ y = 10x — 16 — x^2 \end{cases}$$

Шаг 1: Первая функция — $y = 2\sqrt[3]{x}$

• Это кубический корень, умноженный на 2:

  $$y = 2x^{1/3}$$

• Область определения:
  Кубический корень определён при любом $x \in \mathbb{R}$
• Характер графика:
  • Возрастает на всей области определения
  • Симметричен относительно начала координат
  • Прямая, но слегка изгибается — проходит через (0, 0)

Шаг 2: Вторая функция — $y = 10x — 16 — x^2$

• Преобразуем:

  $$y = -x^2 + 10x — 16$$

• Это парабола, открытая вниз (коэффициент $a = -1$)
• Вершина параболы:

  $$x_0 = -\frac{b}{2a} = -\frac{10}{2 \cdot (-1)} = 5$$ $$y_0 = -5^2 + 10\cdot5 — 16 = -25 + 50 — 16 = 9$$

• Значит, парабола имеет максимум в точке $(5, 9)$
• Таблица значений:

  $$\begin{array}{|c|c|c|c|} \hline x & 6 & 7 & 8 \\ \hline y & 8 & 5 & 0 \\ \hline \end{array}$$

Шаг 3: Решаем систему уравнений

$$2\sqrt[3]{x} = -x^2 + 10x — 16$$

Анализ пересечения графиков

• Функция $y = 2\sqrt[3]{x}$:
  • Возрастает медленно
  • При $x = 0$: $y = 0$
  • При $x = 1$: $y = 2$
  • При $x = 8$: $y = 2 \cdot \sqrt[3]{8} = 2 \cdot 2 = 4$
• Парабола:
  • При $x = 5$: $y = 9$
  • При $x = 6$: $y = 8$
  • При $x = 7$: $y = 5$
  • При $x = 8$: $y = 0$

→ Значит, парабола убывает от $x = 5$ до $x = 8$, и пересекает возрастающую кривую $y = 2\sqrt[3]{x}$ в этом диапазоне

Графически:

• Первая точка пересечения — примерно при $x \approx 1$:
  • $2\sqrt[3]{1} = 2$,
  • Парабола: $10\cdot1 — 16 — 1^2 = 10 — 16 — 1 = -7$ → не подходит
• Пробуем $x = 2$:
  • $y = 2\cdot\sqrt[3]{2} \approx 2 \cdot 1.26 = 2.52$
  • Парабола: $10\cdot2 — 16 — 4 = 20 — 16 — 4 = 0$
• Пробуем $x = 3$:
  • $2\sqrt[3]{3} \approx 2 \cdot 1.44 = 2.88$
  • Парабола: $30 — 16 — 9 = 5$

→ Похоже, пересечение происходит между $x = 2$ и $x = 3$

А также:

• Пробуем $x = 7$:
  • $2\cdot \sqrt[3]{7} \approx 2 \cdot 1.913 = 3.826$
  • Парабола: 5 → выше
• Пробуем $x = 8$:
  • $2 \cdot \sqrt[3]{8} = 4$
  • Парабола: 0 → ниже

→ Второе пересечение между $x = 7$ и $x = 8$

Вывод:

Два пересечения:

• Одно — при $x \in (2, 3)$
• Второе — при $x \in (7, 8)$

Ответ: 2 решения

Итоговые ответы:

а) 1 решение
б) 2 решения