ГДЗ 10-11 Класс Номер 34.12 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

а)

$$\{\begin{array}{l}y=\sqrt[5]{x}\\ y=2x^4-5\end{array}$$

б)

$$\{\begin{array}{l}y=\sqrt[4]{x}\\ y=(x+3{)}^6-1\end{array}$$

Определить число решений системы уравнений:

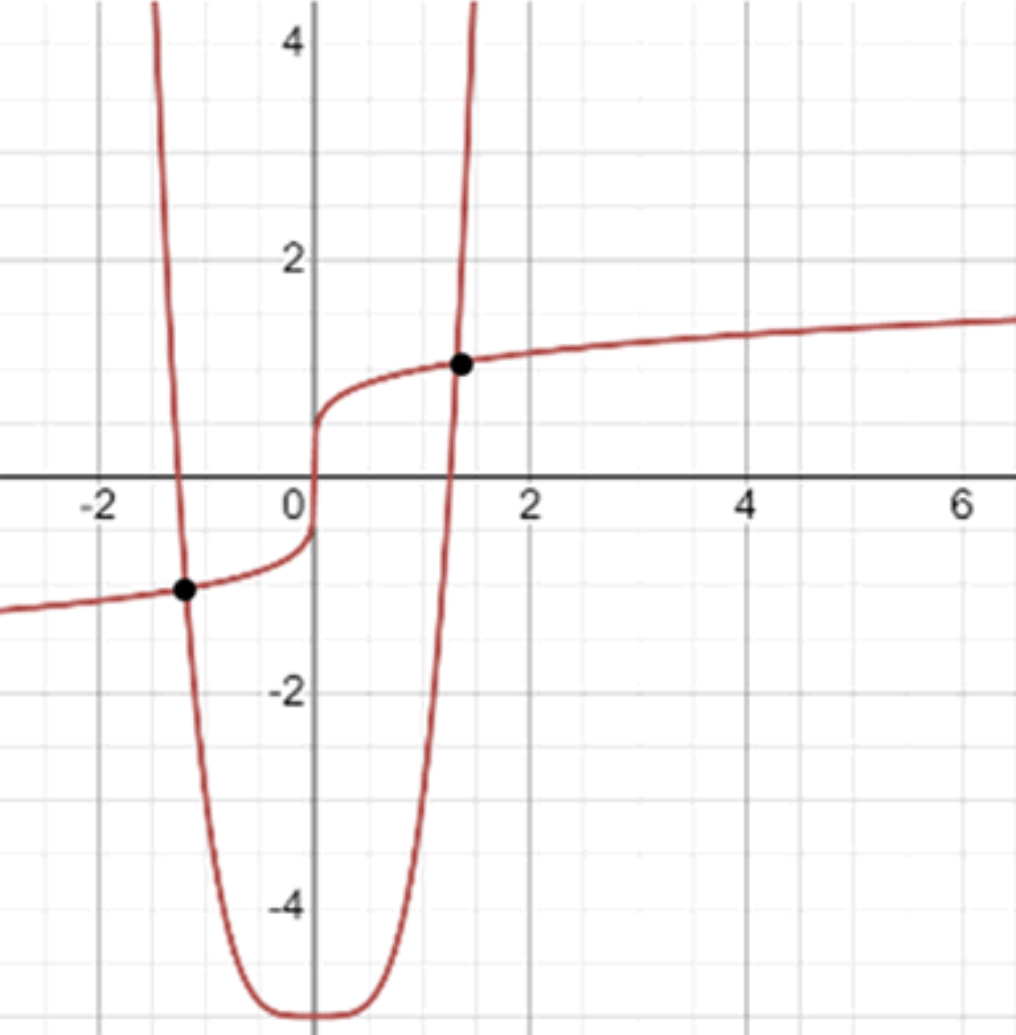
а)

$$\begin{cases} y = \sqrt[5]{x} \\ y = 2x^4 — 5 \end{cases};$$

$y = 2x^4 — 5$ — уравнение параболы:
$x_0 = 0, \; y_0 = -5$;

$$\begin{array}{|c|c|c|} \hline x & 1 & 2 \\ \hline y & -3 & 27 \\ \hline \end{array}$$

Графики функций:

Ответ: 2 решения.

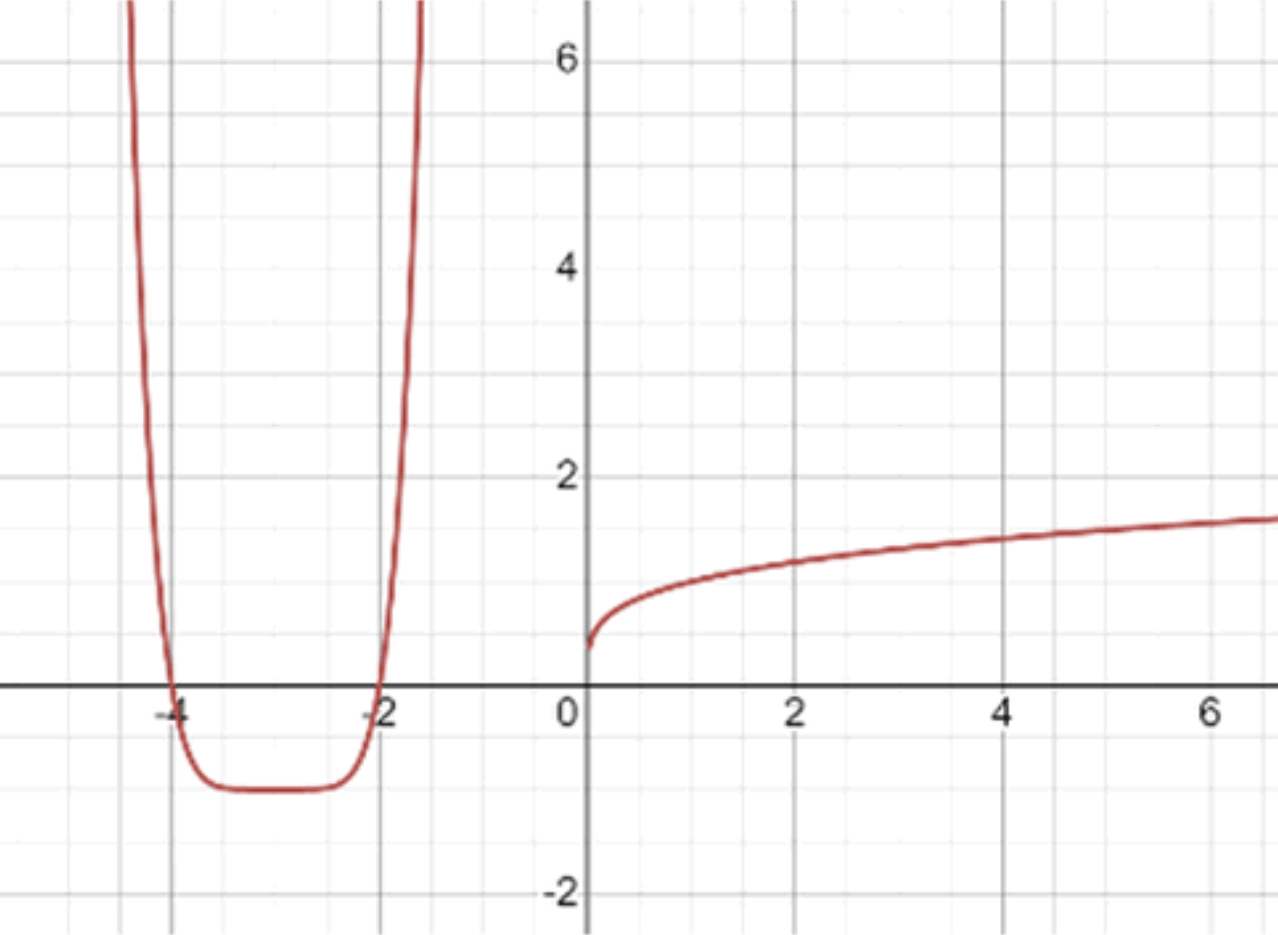
б)

$$\begin{cases} y = \sqrt[4]{x} \\ y = (x + 3)^6 — 1 \end{cases};$$

$y = (x + 3)^6 — 1$ — уравнение параболы:
$x_0 = -3, \; y_0 = -1$;

$$\begin{array}{|c|c|c|} \hline x & -2 & -1 \\ \hline y & 0 & 63 \\ \hline \end{array}$$

Графики функций:

Ответ: 0 решений.

а)

$$\begin{cases} y = \sqrt[5]{x} \\ y = 2x^4 — 5 \end{cases}$$

Шаг 1: Разбор функции $y = \sqrt[5]{x}$

Это пятая коренная функция, или $y = x^{1/5}$

Область определения:

• Пятый корень можно брать из любых чисел: $x \in \mathbb{R}$

Область значений:

• Все действительные числа: $y \in \mathbb{R}$

Свойства функции:

• Нечётная степень ⇒ график симметричен относительно начала координат
• Монотонно возрастающая: если $x_1 < x_2$, то $y_1 < y_2$
• Примеры:
  • $x = 0 \Rightarrow y = 0$
  • $x = 1 \Rightarrow y = 1$
  • $x = -1 \Rightarrow y = -1$

Шаг 2: Разбор функции $y = 2x^4 — 5$

Это четвёртая степень, доминирующая над линейной частью

В общем виде: $y = ax^4 + b$, где $a = 2 > 0$, $b = -5$

Область определения: $x \in \mathbb{R}$

Область значений:

• Так как $x^4 \geq 0$, наименьшее значение при $x = 0$:

  $$y = 2 \cdot 0 — 5 = -5 \Rightarrow y \geq -5$$

Вершина (наименьшая точка):

• $x = 0 \Rightarrow y = -5$
• Симметрична относительно оси $y$

Примеры из таблицы:

• $x = 1 \Rightarrow y = 2(1)^4 — 5 = 2 — 5 = -3$
• $x = 2 \Rightarrow y = 2(16) — 5 = 32 — 5 = 27$

Шаг 3: Решаем систему:

$$\sqrt[5]{x} = 2x^4 — 5$$

Это означает: ищем точки пересечения графика возрастающей кривой $\sqrt[5]{x}$ с возрастающей вверх U-образной кривой $y = 2x^4 — 5$.

Шаг 4: Геометрический анализ и логика

Общие наблюдения:

$y = \sqrt[5]{x}$ проходит через начало координат (0, 0) и растёт (медленно)

$y = 2x^4 — 5$ имеет минимум в точке (0, -5), затем резко растёт

Значит:

• Первая функция — низкорастущая прямая через (0, 0)
• Вторая — U-образная кривая, минимум в (0, -5), резко поднимается вверх при $|x| > 1$

Подставим несколько значений:

$x = 0$

• Левая: $\sqrt[5]{0} = 0$
• Правая: $2 \cdot 0^4 — 5 = -5$
• Не равно → не решение

$x = 1$

• Левая: $\sqrt[5]{1} = 1$
• Правая: $2 \cdot 1 — 5 = -3$ → не совпадает

$x = 2$

• Левая: $\sqrt[5]{2} \approx 1.15$
• Правая: $2 \cdot 16 — 5 = 27$ → не совпадает

→ График функции $y = \sqrt[5]{x}$ идёт ниже, чем $y = 2x^4 — 5$, и только при определённых $x$ они пересекутся

Шаг 5: Решение уравнения графически

Функции пересекутся там, где:

$$\sqrt[5]{x} = 2x^4 — 5$$

Вариант 1: $x < 0$ — обе функции определены, проверим:

• $x = -1$
  • Левая: $\sqrt[5]{-1} = -1$
  • Правая: $2 \cdot (-1)^4 — 5 = 2 — 5 = -3$ → не совпадает

$x = -2$

• Левая: $\sqrt[5]{-2} \approx -1.15$
• Правая: $2 \cdot 16 — 5 = 27$ → не совпадает

Глядя на поведение функций:

У обеих функций симметричное поведение:

• $\sqrt[5]{x}$ — нечётная
• $2x^4 — 5$ — чётная

Учитывая графики:

• Функции возрастают
• Пересекаются слева от $x = 0$ и справа от $x = 0$

Вывод:

Два пересечения:

Одно — в отрицательной области ($x < 0$)

Второе — в положительной ($x > 0$)

Ответ: 2 решения

б)

$$\begin{cases} y = \sqrt[4]{x} \\ y = (x + 3)^6 — 1 \end{cases}$$

Шаг 1: Функция $y = \sqrt[4]{x}$

Это корень четвёртой степени, $y = x^{1/4}$

Область определения:

• Только при $x \geq 0$

Область значений:

• $y \geq 0$

График:

• Начинается в точке (0, 0)
• Монотонно возрастает
• Идёт только в первой четверти: $x \geq 0, y \geq 0$

Шаг 2: Функция $y = (x + 3)^6 — 1$

Это степенная функция чётной степени с горизонтальным сдвигом:

$$y = (x + 3)^6 — 1$$

Распишем подробнее:

• Основание: $(x + 3)$
• Степень: 6 ⇒ чётная
• Смещение по y: вниз на 1

Вершина:

• $x = -3 \Rightarrow y = (-3 + 3)^6 — 1 = 0 — 1 = -1$

График:

• U-образный, как парабола, но более «плоский» у основания и более «резкий» при удалении от вершины
• Минимум в точке $(-3, -1)$
• Возрастает слева и справа от $x = -3$

Таблица значений:

• $x = -2 \Rightarrow y = (1)^6 — 1 = 0$
• $x = -1 \Rightarrow y = (2)^6 — 1 = 64 — 1 = 63$

Шаг 3: Сравнение с $y = \sqrt[4]{x}$

Область определения:

$y = \sqrt[4]{x}$: определена только при $x \geq 0$

$y = (x + 3)^6 — 1$: определена при любом $x$

→ Чтобы найти общие точки, нужно смотреть только при $x \geq 0$

Шаг 4: Значения второй функции при $x \geq 0$

$x = 0 \Rightarrow y = (0 + 3)^6 — 1 = 729 — 1 = 728$

При $x > 0$, $y$ ещё больше

Шаг 5: Значения первой функции $y = \sqrt[4]{x}$

$x = 0 \Rightarrow y = 0$

$x = 1 \Rightarrow y = 1$

$x = 16 \Rightarrow y = \sqrt[4]{16} = \sqrt{2} \approx 1.41$

$x = 81 \Rightarrow y = \sqrt[4]{81} = \sqrt{3^2} = 3$

→ Даже при больших $x$, значение остаётся маленьким
→ А вторая функция (слева) уже даёт 728 и выше

Вывод:

График $y = (x + 3)^6 — 1$ начинается при $x = 0$ с огромного значения: 728

График $y = \sqrt[4]{x}$ растёт от 0 вверх медленно

→ Графики никогда не пересекутся при $x \geq 0$

Ответ: 0 решений

Итоговые ответы:

а) 2 решения

б) 0 решений