ГДЗ 10-11 Класс Номер 34.13 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

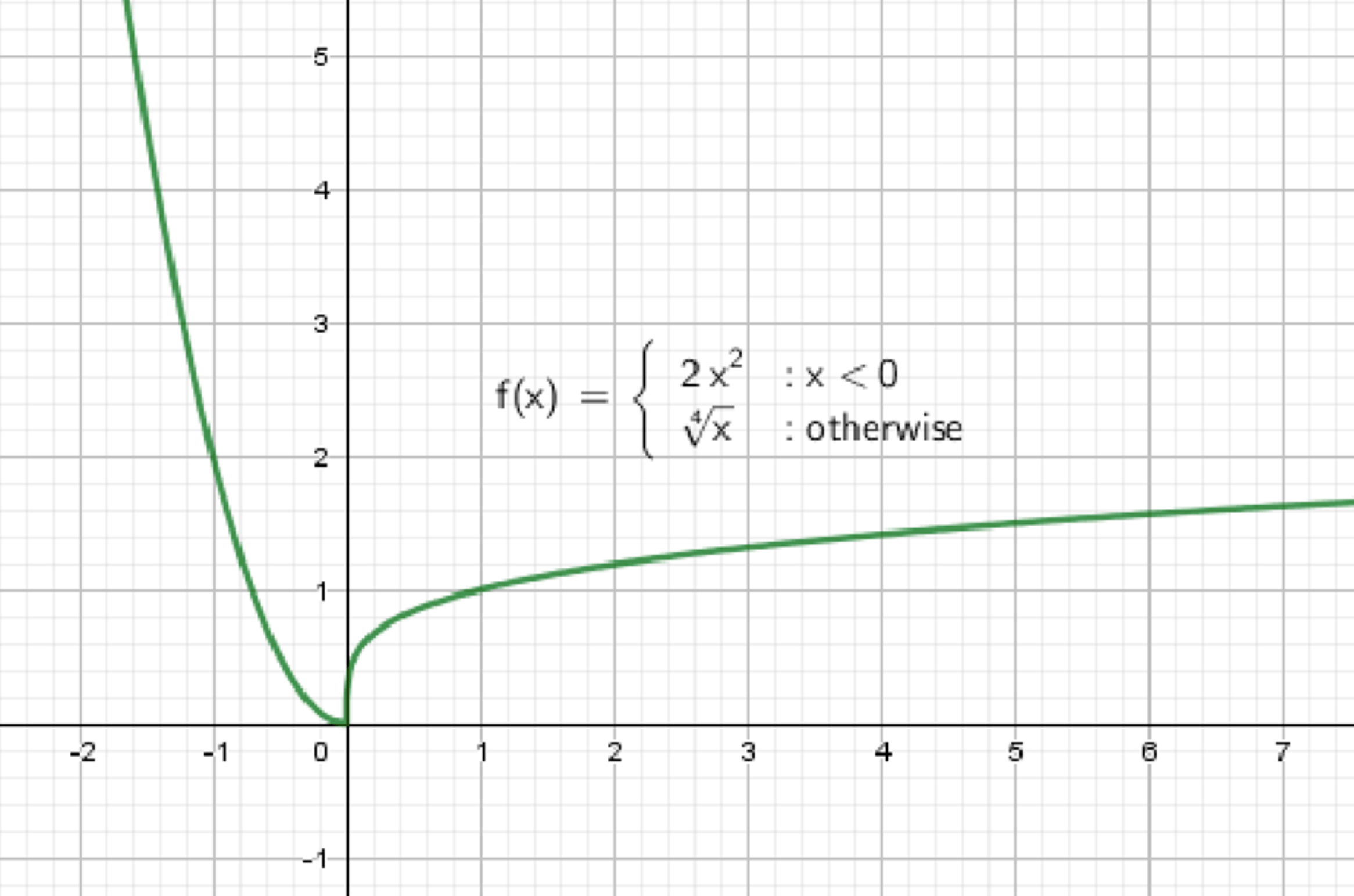
Постройте и прочитайте график функции:

$$y=\{\begin{array}{l}2x^2,\text{ если }x<0\\ \sqrt[4]{x},\text{ если }x\ge 0\end{array}$$

Построить и прочитать график функции:

$$y=\{\begin{array}{l}2x^2,\text{ если }x<0\\ \sqrt[4]{x},\text{ если }x\ge 0\end{array}$$

$y=2x^2$ – уравнение параболы:
$x_0=0,y_0=0$;

$$\overline{)\begin{array}{ccc}x& -2& -1\\ y& 8& 2\end{array}}$$

$y=\sqrt[4]{x}$ – уравнение ветви параболы:

$$\overline{)\begin{array}{cccc}x& 0& 1& 16\\ y& 0& 1& 2\end{array}}$$

График функции:

Свойства функции:
$D(f)=(-\mathrm{\infty };+\mathrm{\infty });$
Ни чётная, ни нечётная;
Убывает на луче $(-\mathrm{\infty };0]$ и возрастает на луче $[0;+\mathrm{\infty });$
Ограничена снизу, не ограничена сверху;
$y_{\text{наим}}=0$ (в точке $x=0$), $y_{\text{наиб}}$ — не существует;
Непрерывна на всей области определения;
$E(f)=[0;+\mathrm{\infty });$
Функция дифференцируема всюду, кроме точки $x=0$

Построить и прочитать график функции:

$$y=\{\begin{array}{ll}2x^2,& \text{если }x<0\\ \sqrt[4]{x},& \text{если }x\ge 0\end{array}$$

Общий план:

Функция определена по частям, то есть мы должны отдельно проанализировать каждую часть (для $x<0$ и для $x\ge 0$), затем выяснить свойства всей функции: область определения, непрерывность, поведение, симметрия, экстремумы, ограниченность, дифференцируемость и область значений.

Часть 1: $y=2x^2$, если $x<0$

1. Тип функции:

Это парабола, стандартного вида:

$$y=a{x}^2\text{при }a=2$$

2. Область определения этой части:

$$x<0$$

3. Основные свойства:

• Ветви направлены вверх, так как $a=2>0$
• Вершина параболы — в точке $(0,0)$, но она не включается в график этой части, т.к. $x<0$
• Функция убывает при движении слева направо к $x=0$

4. Таблица значений (дана):

Пояснение:

• $x=-2$: $y=2(-2{)}^2=8$
• $x=-1$: $y=2(-1{)}^2=2$

5. Поведение около нуля:

• ${\lim }_{x\to 0^{-}}y=2x^2\to 0$
• То есть, слева от 0, график стремится к нулю

Часть 2: $y=\sqrt[4]{x}$, если $x\ge 0$

1. Тип функции:

Корневая функция четвёртой степени, то есть:

$$y=x^{1\mathrm{/}4}$$

2. Область определения:

$$x\ge 0$$

3. Основные свойства:

• Определена только при $x\ge 0$ (четвёртый корень от отрицательных чисел — не определён)
• Значения функции: $y\ge 0$
• Монотонно возрастает — но медленно
• Проходит через точку $(0,0)$

4. Таблица значений (дана):

Пояснение:

• $x=0$: $y=\sqrt[4]{0}=0$
• $x=1$: $y=\sqrt[4]{1}=1$
• $x=16$: $\sqrt[4]{16}=\sqrt{\sqrt{16}}=\sqrt{4}=2$

5. Поведение:

• Функция возрастает на всей своей области определения
• При $x\to +\mathrm{\infty }$, $y\to +\mathrm{\infty }$, но очень медленно

Точка склейки: $x=0$

Проверим значение функции в этой точке:

• Слева: ${\lim }_{x\to 0^{-}}2x^2=0$
• Справа: $y=\sqrt[4]{0}=0$

Значит, график не имеет разрыва в точке $x=0$
Функция непрерывна в этой точке

График

График функции состоит из двух частей, которые соединяются в точке $(0,0)$:

Левая часть (при $x<0$):

• Форма восходящей параболы, но изображается только левая половина
• Начинается где-то вверху слева и убывает по мере приближения к 0
• Не включает саму точку $x=0$, но стремится к ней

Правая часть (при $x\ge 0$):

• Медленно возрастающая корневая кривая
• Проходит через (0, 0), (1, 1), (16, 2)
• График идет вправо, медленно поднимаясь

Свойства функции

1. Область определения (D(f)):

Функция задана при всех $x\in \mathbb{R}$:

$$D(f)=(-\mathrm{\infty };+\mathrm{\infty })$$

2. Область значений (E(f)):

Так как обе части принимают только значения $y\ge 0$:

$$E(f)=[0;+\mathrm{\infty })$$

3. Чётность/нечётность:

• Функция не симметрична относительно оси $y$
• Не удовлетворяет условиям:
  • $f(-x)=f(x)$ (нечётная)
  • $f(-x)=-f(x)$ (чётная)

Функция ни чётная, ни нечётная

4. Монотонность:

• Убывает на интервале $(-\mathrm{\infty };0)$
• Возрастает на интервале $(0;+\mathrm{\infty })$
• Точка $x=0$ — переход от убывания к возрастанию

5. Ограниченность:

• Снизу ограничена: $y\ge 0$
• Сверху — не ограничена

6. Наименьшее значение:

• Достигается в точке $x=0$

$$y_{\text{наим}}=0$$

7. Наибольшего значения нет:

• При $x\to \pm \mathrm{\infty }$, $y\to +\mathrm{\infty }$

8. Непрерывность:

• Функция непрерывна на всей области определения, включая точку $x=0$

9. Дифференцируемость:

• Обе части по отдельности дифференцируемы
• В точке $x=0$:
  • Левая производная:$$f_{-}^{\mathrm{\prime }}(0)=\underset{x\to 0^{-}}{\lim }\frac{f(x)-f(0)}{x-0}=\underset{x\to 0^{-}}{\lim }\frac{2x^2-0}{x}=\underset{x\to 0^{-}}{\lim }2x=0$$
  • Правая производная:$$f_{+}^{\mathrm{\prime }}(0)=\underset{x\to 0^{+}}{\lim }\frac{x^{1\mathrm{/}4}}{x}=\underset{x\to 0^{+}}{\lim }{x}^{-3\mathrm{/}4}=+\mathrm{\infty }$$

    (→ не существует как конечное число)

Функция не дифференцируема в точке $x=0$