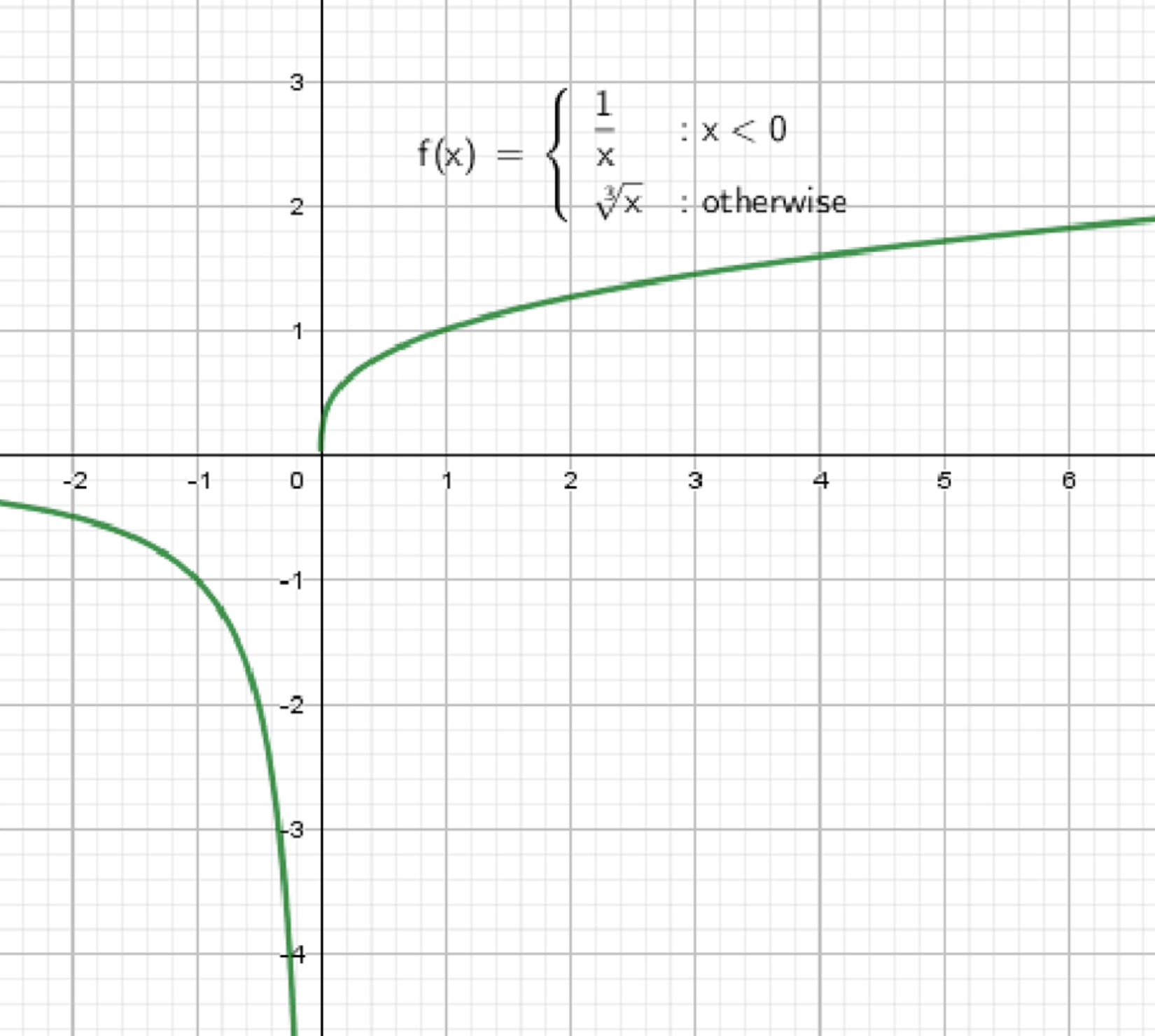ГДЗ 10-11 Класс Номер 34.14 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте и прочитайте график функции:

$$y=\{\begin{array}{l}\frac{3}{x},\text{ если }x<0\\ \sqrt[3]{x},\text{ если }x\ge 0\end{array}$$

Построить и прочитать график функции:

$$y = \begin{cases} \frac{3}{x}, \text{ если } x < 0 \\ \sqrt[3]{x}, \text{ если } x \geq 0 \end{cases}$$

$y = \frac{3}{x}$ — уравнение гиперболы:
$x_0 = 0, \; y_0 = 0$;

$$\begin{array}{|c|c|c|} \hline x & -3 & -1 \\ \hline y & -1 & -3 \\ \hline \end{array}$$

$y = \sqrt[3]{x}$ — уравнение ветви параболы:

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 8 \\ \hline y & 0 & 1 & 2 \\ \hline \end{array}$$

График функции:

Свойства функции:
$D(f) = (-\infty; +\infty)$;
Ни чётная, ни нечётная;
Убывает на интервале $(-\infty; 0)$ и возрастает на луче $[0; +\infty)$;
Имеет горизонтальную асимптоту $\lim_{x \to -\infty} f(x) = 0$;
Имеет вертикальную асимптоту $x = 0$;
Не ограничена снизу, не ограничена сверху;
$y_{\text{наим}}$ — не существует, $y_{\text{наиб}}$ — не существует;
Непрерывна на интервалах $(-\infty; 0) \cup (0; +\infty)$;
$E(f) = (-\infty; +\infty)$;
Функция дифференцируема всюду, кроме точки $x = 0$

Построить и прочитать график функции:

$$y = \begin{cases} \frac{3}{x}, & \text{если } x < 0 \\ \sqrt[3]{x}, & \text{если } x \geq 0 \end{cases}$$

Это кусочно-заданная функция, составленная из двух выражений:

• Для $x < 0$: $y = \frac{3}{x}$
• Для $x \geq 0$: $y = \sqrt[3]{x}$

Анализ первой части:

$$y = \frac{3}{x}, \quad \text{если } x < 0$$

1. Тип функции:

• Это гипербола, то есть рациональная функция вида $y = \frac{k}{x}$, с коэффициентом $k = 3$

2. Область определения:

• В данной части: $x < 0$

3. Характер поведения:

• Значения $y$ отрицательные, так как $\frac{3}{x} < 0$ при $x < 0$
• При приближении к нулю слева:

  $$\lim_{x \to 0^-} \frac{3}{x} = -\infty$$

• При $x \to -\infty$:

  $$\lim_{x \to -\infty} \frac{3}{x} = 0^-$$

  То есть $y \to 0$ снизу

4. Таблица значений (из условия):

Пояснение:

• $\frac{3}{-3} = -1$
• $\frac{3}{-1} = -3$

5. Асимптоты:

• Вертикальная асимптота: $x = 0$ (график не существует в этой точке)
• Горизонтальная асимптота: $y = 0$ (при $x \to -\infty$)

Анализ второй части:

$$y = \sqrt[3]{x}, \quad \text{если } x \geq 0$$

1. Тип функции:

• Кубический корень — $y = x^{1/3}$

2. Область определения:

• В данной части: $x \geq 0$
• Функция определена при любом $x \in \mathbb{R}$, но здесь ограничена условием $x \geq 0$

3. Характер поведения:

• Функция неограниченно возрастает при $x \to +\infty$
• Возрастает монотонно
• При $x = 0$: $y = 0$
• При $x \to +\infty$: $y \to +\infty$

4. Таблица значений (из условия):

Пояснение:

• $\sqrt[3]{0} = 0$
• $\sqrt[3]{1} = 1$
• $\sqrt[3]{8} = 2$

5. Свойства:

• Функция непрерывна и дифференцируема на $(0; +\infty)$
• В точке $x = 0$:

  $$y = 0, \quad y’ = \frac{1}{3x^{2/3}} \Rightarrow \text{неопределена при } x = 0$$

Склейка графика в точке $x = 0$:

• Левая часть:

  $$\lim_{x \to 0^-} \frac{3}{x} = -\infty$$

• Правая часть:

  $$\lim_{x \to 0^+} \sqrt[3]{x} = 0$$

→ График разорван в точке $x = 0$, то есть:

• Разрыв второго рода
• Нет значения функции в точке $x = 0$ для левой части
• Есть значение в правой части: $f(0) = 0$

График:

Для $x < 0$:

• Гиперболическая ветвь в третьей четверти
• При $x \to -\infty$, график приближается к оси $x$ снизу
• При $x \to 0^-$, график уходит вниз в бесконечность
• Резко убывает

Для $x \geq 0$:

• Кривая плавно поднимается вправо
• Стартует из точки $(0, 0)$
• Примеры: проходит через (1, 1), (8, 2)
• Рост замедляется при больших $x$

Свойства функции (по пунктам):

1. Область определения:

• Гипербола: $x < 0$
• Корень: $x \geq 0$

$$D(f) = (-\infty; 0) \cup [0; +\infty) = (-\infty; +\infty)$$

2. Область значений:

• Обе части функции могут принимать любые действительные значения

$$E(f) = (-\infty; +\infty)$$

3. Нечётность/чётность:

• Проверка:
  • $f(-x) = \frac{3}{-x} = -\frac{3}{x}$ при $x > 0$
  • $f(x) = \sqrt[3]{x} \ne -f(-x)$
• Функция не является чётной или нечётной

4. Монотонность:

• Убывает на $(-\infty; 0)$
• Возрастает на $[0; +\infty)$

5. Ограниченность:

• Не ограничена снизу:

  $$\lim_{x \to 0^-} \frac{3}{x} = -\infty$$

• Не ограничена сверху:

  $$\lim_{x \to +\infty} \sqrt[3]{x} = +\infty$$

6. Асимптоты:

• Горизонтальная асимптота:

  $$\lim_{x \to -\infty} \frac{3}{x} = 0 \Rightarrow y = 0$$

• Вертикальная асимптота:

  $$\lim_{x \to 0^-} \frac{3}{x} = -\infty \Rightarrow x = 0$$

7. Наибольшее и наименьшее значения:

• Ни $y_{\text{наим}}$, ни $y_{\text{наиб}}$ не существуют

8. Непрерывность:

• Функция непрерывна на промежутках:

  $$(-\infty; 0) \quad \text{и} \quad (0; +\infty)$$

• В точке $x = 0$ — разрыв второго рода

9. Дифференцируемость:

• Функция дифференцируема:
  • На $(-\infty; 0)$
  • На $(0; +\infty)$
• Не дифференцируема в точке $x=0$$x = 0$