ГДЗ 10-11 Класс Номер 34.15 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

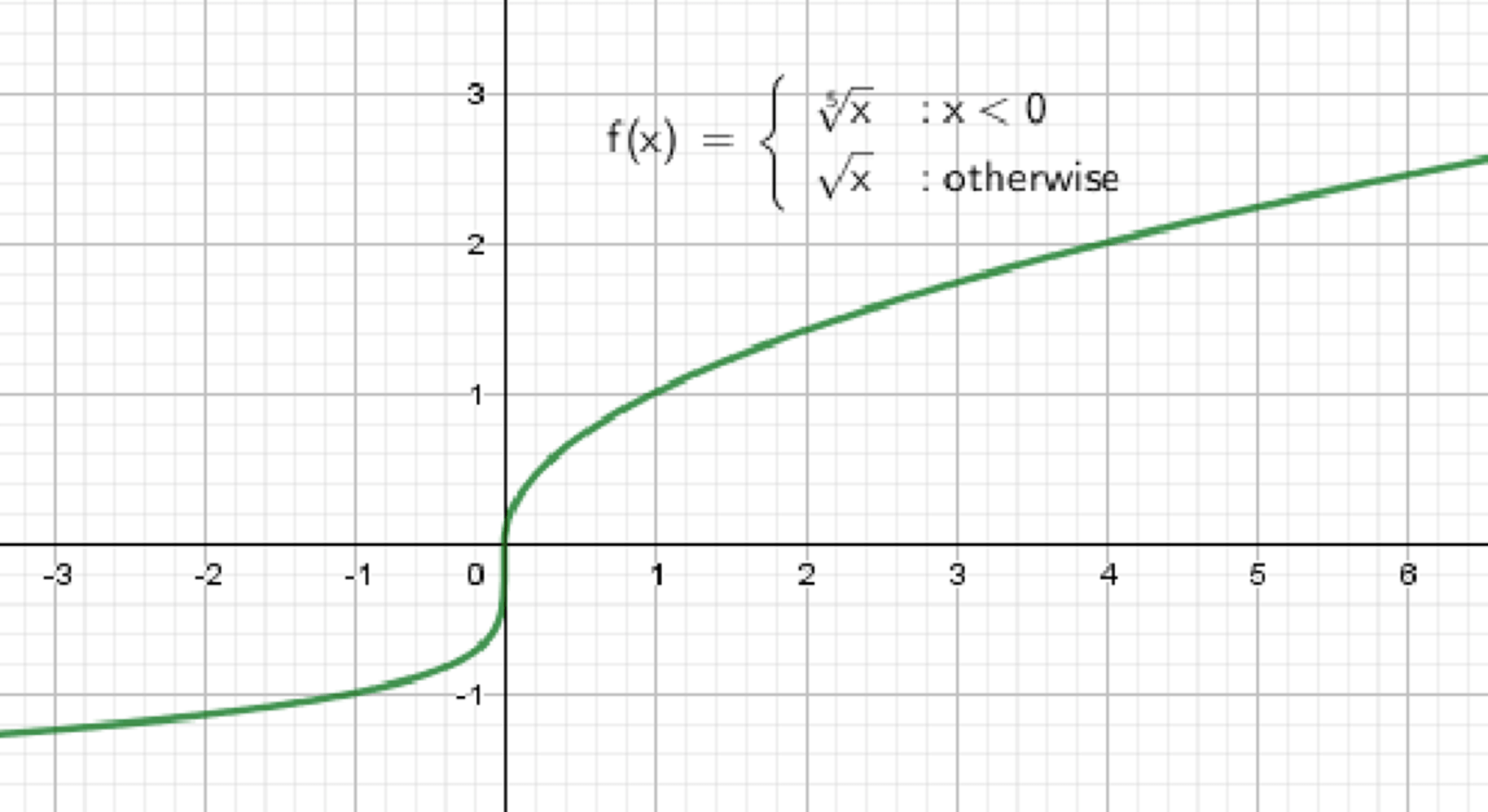
Постройте и прочитайте график функции:

$$y=\{\begin{array}{l}\sqrt[5]{x},\text{ если }x<0\\ \sqrt{x},\text{ если }x\ge 0\end{array}$$

Построить и прочитать график функции:

$$y = \begin{cases} \sqrt[5]{x}, \text{ если } x < 0 \\ \sqrt{x}, \text{ если } x \geq 0 \end{cases}$$

$y = \sqrt[5]{x}$ — уравнение ветви параболы:

$$\begin{array}{|c|c|c|c|} \hline x & -32 & -1 & 0 \\ \hline y & -2 & -1 & 0 \\ \hline \end{array}$$

$y = \sqrt{x}$ — уравнение ветви параболы:

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 4 \\ \hline y & 0 & 1 & 2 \\ \hline \end{array}$$

График функции:

Свойства функции:
$D(f) = (-\infty; +\infty)$;
Ни чётная, ни нечётная;
Возрастает на всей числовой прямой;
Не ограничена снизу, не ограничена сверху;
$y_{\min}$ — не существует, $y_{\max}$ — не существует;
Непрерывна на всей области определения;
$E(f) = (-\infty; +\infty)$;
Функция дифференцируема во всех точках

Построить и прочитать график функции:

$$y = \begin{cases} \sqrt[5]{x}, & \text{если } x < 0 \\ \sqrt{x}, & \text{если } x \geq 0 \end{cases}$$

Анализ первой части:

$$y = \sqrt[5]{x}, \quad \text{если } x < 0$$

1. Тип функции:

• Это корневая функция нечетной степени: $y = x^{1/5}$

2. Область определения:

• Функция определена при всех $x \in \mathbb{R}$
• В данной части: только при $x < 0$

3. Область значений:

• Значения также любые: $y \in \mathbb{R}$

4. Поведение:

• Монотонно возрастает (при $x$ от $-\infty$ до 0)
• При $x \to -\infty$, $y \to -\infty$
• При $x \to 0^-$, $y \to 0^-$

5. Таблица значений (из условия):

$$\begin{array}{|c|c|c|c|} \hline x & -32 & -1 & 0 \\ \hline y & -2 & -1 & 0 \\ \hline \end{array}$$

Пояснение:

• $\sqrt[5]{-32} = -2$
• $\sqrt[5]{-1} = -1$
• $\lim_{x \to 0^-} \sqrt[5]{x} = 0$

6. График:

• Гладкая, плавно возрастающая кривая, расположенная в третьей четверти
• Подходит к началу координат с отрицательных значений
• График не разрывается и не обрывается

Анализ второй части:

$$y = \sqrt{x}, \quad \text{если } x \geq 0$$

1. Тип функции:

• Корневая функция второй степени: $y = x^{1/2}$

2. Область определения:

• $x \geq 0$

3. Область значений:

• $y \geq 0$

4. Поведение:

• Монотонно возрастает
• При $x = 0$, $y = 0$
• При $x \to +\infty$, $y \to +\infty$

5. Таблица значений (из условия):

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 4 \\ \hline y & 0 & 1 & 2 \\ \hline \end{array}$$

Пояснение:

• $\sqrt{0} = 0$
• $\sqrt{1} = 1$
• $\sqrt{4} = 2$

6. График:

• Гладкая, возрастающая кривая в первой четверти
• Начинается в точке (0, 0)
• Рост замедляется при увеличении $x$

Склейка графика в точке $x = 0$

• Левая часть при $x \to 0^-$: $\sqrt[5]{x} \to 0$
• Правая часть при $x = 0$: $\sqrt{0} = 0$

→ Значения совпадают в точке $x = 0$
→ Функция непрерывна в точке $x = 0$

График функции:

• Для $x < 0$:
  — График расположен в третьей четверти
  — Плавно поднимается к точке (0, 0), не обрываясь
  — Кривая медленно возрастает
• Для $x \geq 0$:
  — График в первой четверти
  — Начинается из точки (0, 0)
  — Плавно возрастает вправо
  — Проходит через точки (1, 1) и (4, 2)
• Вся функция — неразрывная и гладкая кривая, идущая из третьей четверти через начало координат в первую четверть

Анализ свойств функции:

1. Область определения:

Функция задана на всей числовой прямой:

$$D(f) = (-\infty; +\infty)$$

2. Область значений:

• Левая часть: $y \to -\infty$ при $x \to -\infty$
• Правая часть: $y \to +\infty$ при $x \to +\infty$

$$E(f) = (-\infty; +\infty)$$

3. Монотонность:

• Обе части монотонно возрастают
• Следовательно, вся функция возрастает на всей числовой прямой

4. Чётность / нечётность:

Проверим:

• $f(-x) \ne f(x)$
• $f(-x) \ne -f(x)$

Пример:

• $f(-1) = \sqrt[5]{-1} = -1$
• $f(1) = \sqrt{1} = 1$

→ Функция нечётной и не чётной

5. Ограниченность:

• Не ограничена снизу: при $x \to -\infty$, $y \to -\infty$
• Не ограничена сверху: при $x \to +\infty$, $y \to +\infty$

6. Наибольшее и наименьшее значения:

• Нет точек максимума и минимума:

  $$y_{\min} \text{ — не существует}, \quad y_{\max} \text{ — не существует}$$

7. Непрерывность:

• Функция непрерывна:
  • На $(-\infty; 0)$
  • На $(0; +\infty)$
  • В точке $x = 0$:

    $$\lim_{x \to 0^-} \sqrt[5]{x} = 0, \quad \sqrt{0} = 0$$

    Значение функции совпадает с пределом
    → Непрерывна на всей области определения

8. Дифференцируемость:

Проверим в точке $x = 0$:

• Левая производная:

  $$f’_-(0) = \lim_{x \to 0^-} \frac{\sqrt[5]{x} — 0}{x — 0} = \lim_{x \to 0^-} \frac{x^{1/5}}{x} = \lim_{x \to 0^-} x^{-4/5} \to +\infty$$

• Правая производная:

  $$f’_+(0) = \lim_{x \to 0^+} \frac{\sqrt{x} — 0}{x — 0} = \lim_{x \to 0^+} \frac{x^{1/2}}{x} = \lim_{x \to 0^+} x^{-1/2} \to +\infty$$

Функция дифференцируема во всех точках