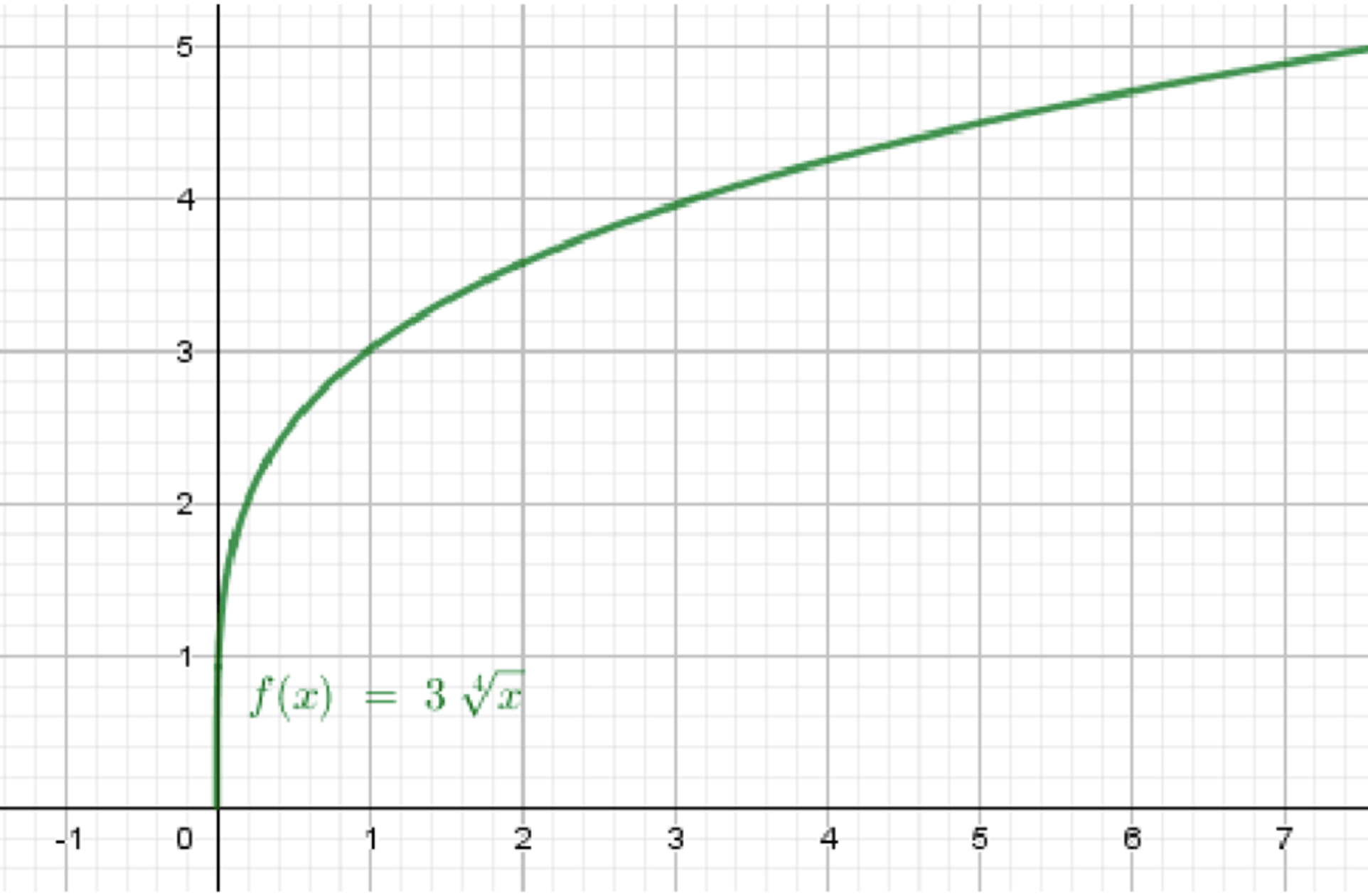ГДЗ 10-11 Класс Номер 34.2 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

а) $y = 2\sqrt[3]{x}$

б) $y = -\dfrac{1}{3}\sqrt[6]{x}$

в) $y = -\dfrac{1}{2}\sqrt[3]{x}$

г) $y = 3\sqrt[4]{x}$

Построить график функции:

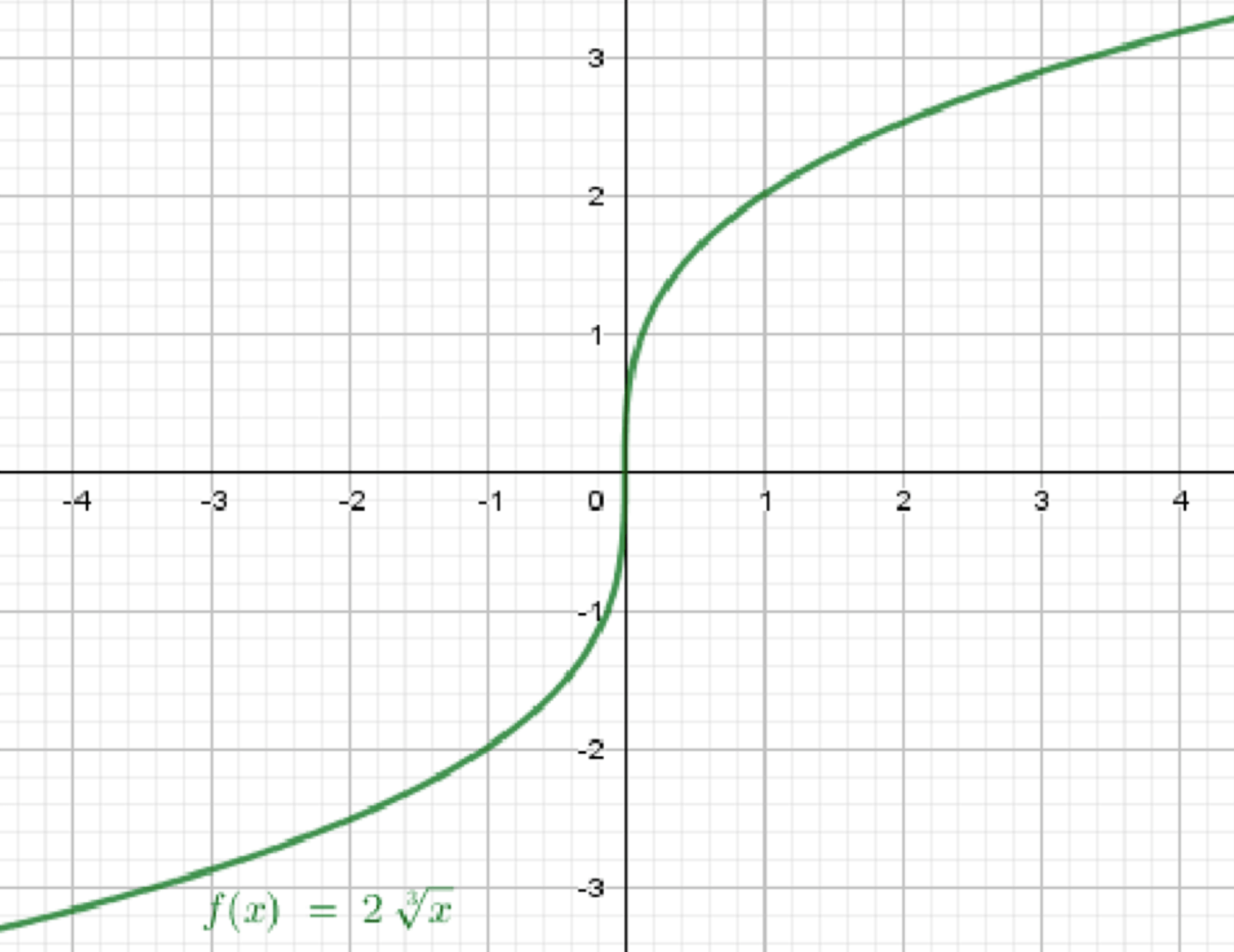
а) $y = 2\sqrt[3]{x}$
Построим график функции $y = \sqrt[3]{x}$;
Растянем его в два раза от оси абсцисс.

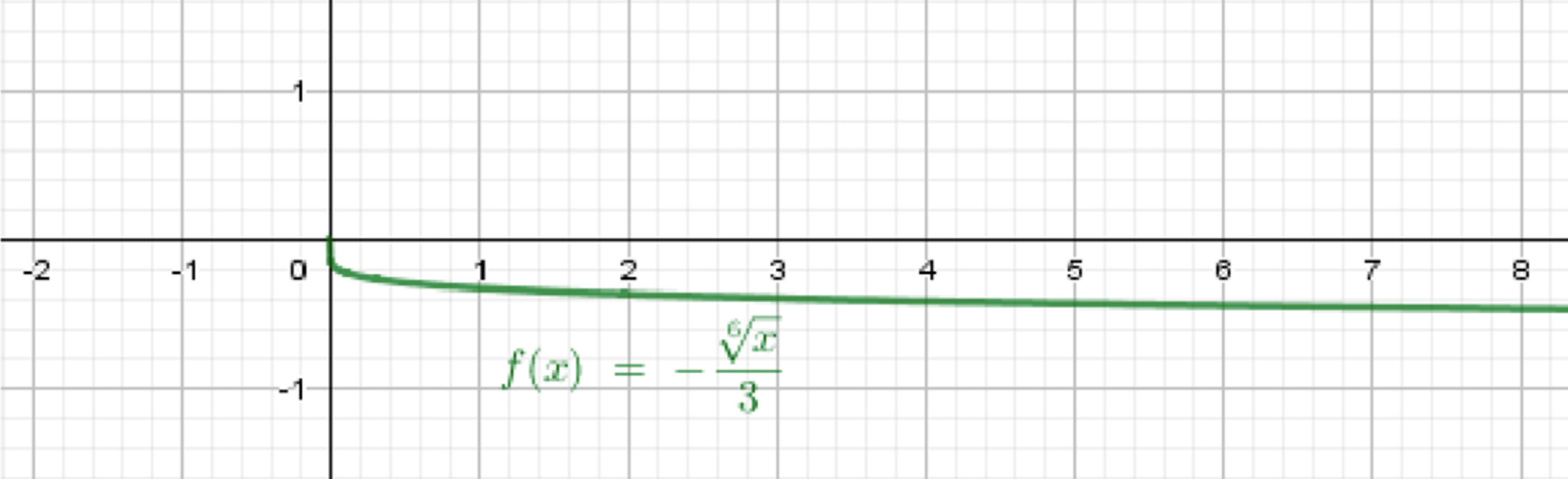
б) $y = -\dfrac{1}{3}\sqrt[6]{x}$
Построим график функции $y = \sqrt[6]{x}$;
Отразим его относительно оси абсцисс;
Сожмем его в три раза к оси абсцисс.

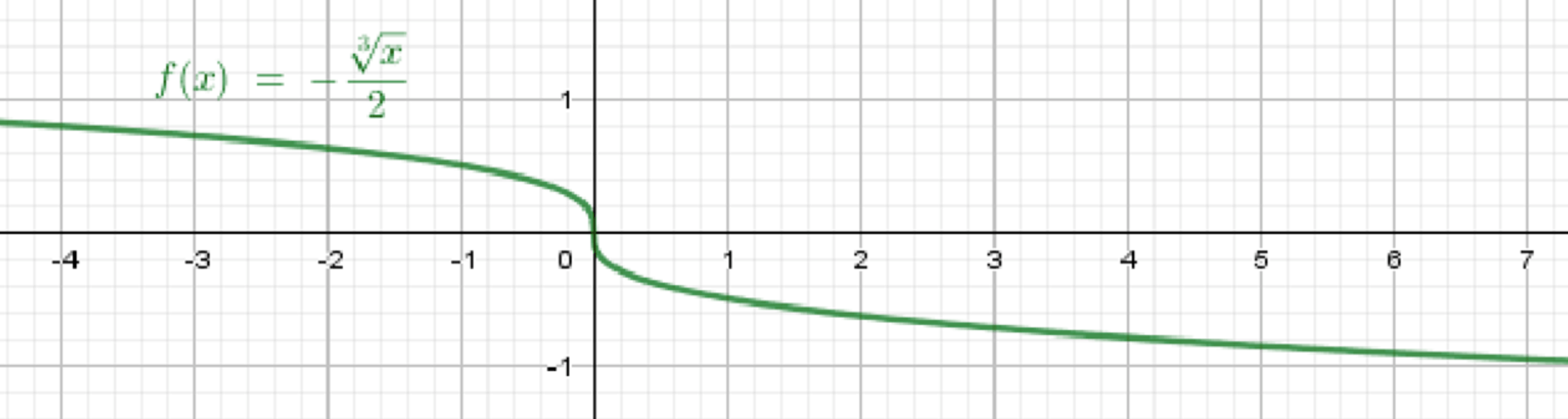
в) $y = -\dfrac{1}{2}\sqrt[3]{x}$
Построим график функции $y = \sqrt[3]{x}$;
Отразим его относительно оси абсцисс;
Сожмем его в два раза к оси абсцисс.

г) $y = 3\sqrt[4]{x}$
Построим график функции $y = \sqrt[4]{x}$;
Растянем его в три раза от оси абсцисс.

а) $y = 2\sqrt[3]{x}$

Базовая функция:
$y = \sqrt[3]{x}$

Шаг 1. Построение базового графика

• График $y = \sqrt[3]{x}$ проходит через точки:
  $(-8; -2),\ (-1; -1),\ (0; 0),\ (1; 1),\ (8; 2)$
• Функция нечётная (симметрична относительно начала координат)
• Область определения: $\mathbb{R}$
• Значения растут монотонно

Шаг 2. Умножение функции на 2
Модификация $y = 2\sqrt[3]{x}$ означает растяжение графика в 2 раза от оси абсцисс (вверх и вниз).
Каждое значение $y$ становится в 2 раза больше.

Преобразованные точки:

• $x = -8 \Rightarrow y = 2 \cdot (-2) = -4$
• $x = -1 \Rightarrow y = 2 \cdot (-1) = -2$
• $x = 0 \Rightarrow y = 0$
• $x = 1 \Rightarrow y = 2 \cdot 1 = 2$
• $x = 8 \Rightarrow y = 2 \cdot 2 = 4$

Вывод:
График имеет ту же форму, что $\sqrt[3]{x}$, но вытянут вверх и вниз в 2 раза.

б) $y = -\dfrac{1}{3}\sqrt[6]{x}$

Базовая функция:
$y = \sqrt[6]{x}$

Шаг 1. Построение базового графика

• Определена только при $x \geq 0$
• Проходит через точки:
  $(0; 0),\ (1; 1),\ (64; 2)$
• Гладко и монотонно возрастает, очень медленно

Шаг 2. Умножение на -1
Модификация $y = -\sqrt[6]{x}$ означает отражение графика относительно оси абсцисс.

Шаг 3. Умножение на $\frac{1}{3}$
Модификация $y = -\dfrac{1}{3}\sqrt[6]{x}$ означает сжатие графика в 3 раза к оси абсцисс, после отражения.

Преобразованные точки:

• $x = 0 \Rightarrow y = 0$
• $x = 1 \Rightarrow y = -\dfrac{1}{3} \cdot 1 = -\dfrac{1}{3}$
• $x = 64 \Rightarrow y = -\dfrac{1}{3} \cdot 2 = -\dfrac{2}{3}$

Вывод:
График расположен в четвёртой четверти, медленно убывает, при этом в 3 раза ближе к оси абсцисс, чем базовая функция.

в) $y = -\dfrac{1}{2}\sqrt[3]{x}$

Базовая функция:
$y = \sqrt[3]{x}$

Шаг 1. Построение базового графика
(см. пункт а)

Шаг 2. Умножение на -1
Отражение относительно оси абсцисс

Шаг 3. Умножение на $\frac{1}{2}$
Сжатие к оси абсцисс в 2 раза

Преобразованные точки:

• $x = -8 \Rightarrow y = -\dfrac{1}{2} \cdot (-2) = 1$
• $x = -1 \Rightarrow y = -\dfrac{1}{2} \cdot (-1) = 0{,}5$
• $x = 0 \Rightarrow y = 0$
• $x = 1 \Rightarrow y = -\dfrac{1}{2} \cdot 1 = -0{,}5$
• $x = 8 \Rightarrow y = -\dfrac{1}{2} \cdot 2 = -1$

Вывод:
График симметричен базовому, но перевернут и сжат в 2 раза по вертикали. Лежит в II и IV четвертях.

г) $y = 3\sqrt[4]{x}$

Базовая функция:
$y = \sqrt[4]{x}$

Шаг 1. Построение базового графика

• Определён при $x \geq 0$
• Проходит через точки:
  $(0; 0),\ (1; 1),\ (16; 2)$

Шаг 2. Умножение на 3
Означает растяжение графика в 3 раза от оси абсцисс

Преобразованные точки:

• $x = 0 \Rightarrow y = 0$
• $x = 1 \Rightarrow y = 3 \cdot 1 = 3$
• $x = 16 \Rightarrow y = 3 \cdot 2 = 6$

Вывод:
График лежит в первой четверти, как и базовая функция, но растет быстрее, в 3 раза выше.