ГДЗ 10-11 Класс Номер 34.25 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $$$y=\sqrt[3]{\frac{x^2-5x+4}{x-4}}$

б) $$$y=\sqrt[4]{\frac{x^2-x-6}{x-3}}$

Построить график функции:

а) $$$y = \sqrt[3]{\frac{x^2 — 5x + 4}{x — 4}} = \sqrt[3]{\frac{(x — 1)(x — 4)}{x — 4}} = \sqrt[3]{x — 1}$;

Разложим числитель на множители:

$x^2 — 5x + 4 = 0$;

$D = 5^2 — 4 \cdot 4 = 25 — 16 = 9$, тогда:

$x_1 = \frac{5 — 3}{2} = 1$ и $x_2 = \frac{5 + 3}{2} = 4$;

Выражение имеет смысл при:

$x — 4 \ne 0$;

$x \ne 4$;

График функции:

б) $$$y = \sqrt[4]{\frac{x^2 — x — 6}{x — 3}} = \sqrt[4]{\frac{(x + 2)(x — 3)}{x — 3}} = \sqrt[4]{x + 2}$;

Разложим числитель на множители:

$x^2 — x — 6 = 0$;

$D = 1^2 + 4 \cdot 6 = 1 + 24 = 25$, тогда:

$x_1 = \frac{1 — 5}{2} = -2$ и $x_2 = \frac{1 + 5}{2} = 3$;

Выражение имеет смысл при:

$x — 3 \ne 0$;

$x \ne 3$;

График функции:

а) $y = \sqrt[3]{\frac{x^2 — 5x + 4}{x — 4}}$

Шаг 1: Разложим числитель на множители

$$x^2 — 5x + 4$$

Вычислим дискриминант:

$$D = (-5)^2 — 4 \cdot 1 \cdot 4 = 25 — 16 = 9$$

Находим корни:

$$x_1 = \frac{5 — \sqrt{9}}{2} = \frac{5 — 3}{2} = 1, \quad x_2 = \frac{5 + \sqrt{9}}{2} = \frac{5 + 3}{2} = 4$$

Итак:

$$x^2 — 5x + 4 = (x — 1)(x — 4)$$

Шаг 2: Сократим дробь

Подставим:

$$y = \sqrt[3]{\frac{(x — 1)(x — 4)}{x — 4}}$$

При $x \ne 4$, можно сократить:

$$y = \sqrt[3]{x — 1}, \quad x \ne 4$$

Шаг 3: Область определения

• Корень нечетной степени (3) — определён при любых значениях выражения под корнем.
• Единственное ограничение: нельзя делить на 0, то есть:

$$x — 4 \ne 0 \Rightarrow x \ne 4$$

Шаг 4: Конечный вид функции

$$y = \sqrt[3]{x — 1}, \quad x \ne 4$$

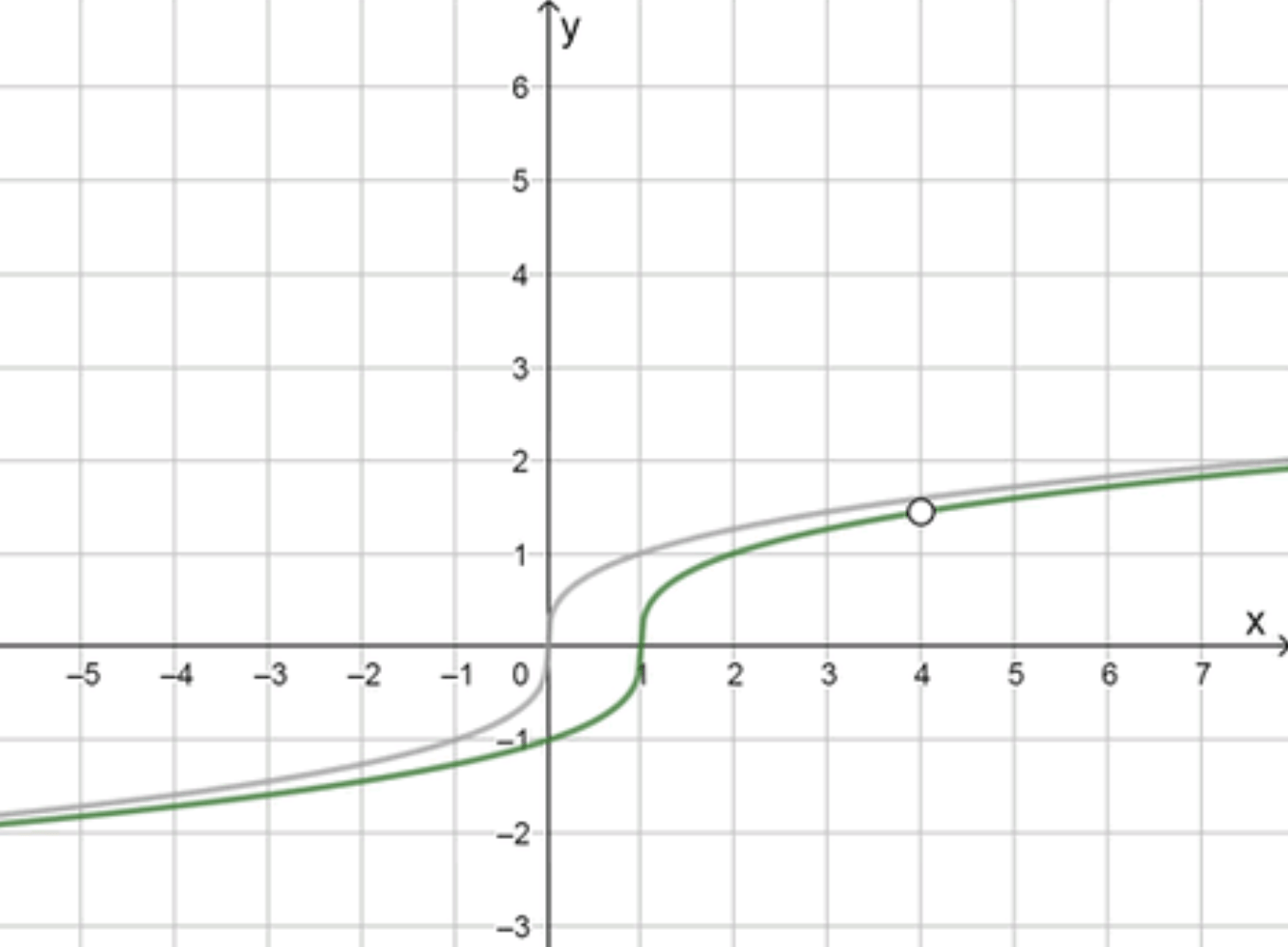
Это кубический корень, смещённый на 1 единицу вправо по оси $x$, с удалённой точкой при $x = 4$ (вырожденная точка).

Шаг 5: Поведение и свойства графика

• График похож на $y = \sqrt[3]{x}$, но сдвинут на 1 единицу вправо:
  • Точка перегиба находится в $x = 1$, $y = 0$
• Область определения:

  $$D(y) = (-\infty; 4) \cup (4; +\infty)$$

• Область значений: кубический корень может принимать любые значения:

  $$E(y) = (-\infty; +\infty)$$

• В точке $x = 4$ — удалённая точка, на графике будет разрыв (дырка).
• График плавно возрастает слева направо.

Вывод:

График функции — это график $y = \sqrt[3]{x — 1}$ без точки $x = 4$.
В этой точке есть разрыв второго рода (в выражении был делитель ноль, но корень существовал).

б) $y = \sqrt[4]{\frac{x^2 — x — 6}{x — 3}}$

Шаг 1: Разложим числитель на множители

$$x^2 — x — 6$$

Найдём дискриминант:

$$D = (-1)^2 — 4 \cdot 1 \cdot (-6) = 1 + 24 = 25$$

Корни:

$$x_1 = \frac{1 — 5}{2} = -2, \quad x_2 = \frac{1 + 5}{2} = 3$$

Разложение:

$$x^2 — x — 6 = (x + 2)(x — 3)$$

Шаг 2: Сокращение дроби

$$y = \sqrt[4]{\frac{(x + 2)(x — 3)}{x — 3}} = \sqrt[4]{x + 2}, \quad x \ne 3$$

Потому что $x — 3 \ne 0 \Rightarrow x \ne 3$

Шаг 3: Область определения

• Корень четвёртой степени — подкоренное выражение должно быть неотрицательным:

$$x + 2 \geq 0 \Rightarrow x \geq -2$$

Но также:

$$x \ne 3$$

Шаг 4: Конечный вид функции

$$y = \sqrt[4]{x + 2}, \quad x \geq -2, \ x \ne 3$$

Шаг 5: Поведение и свойства графика

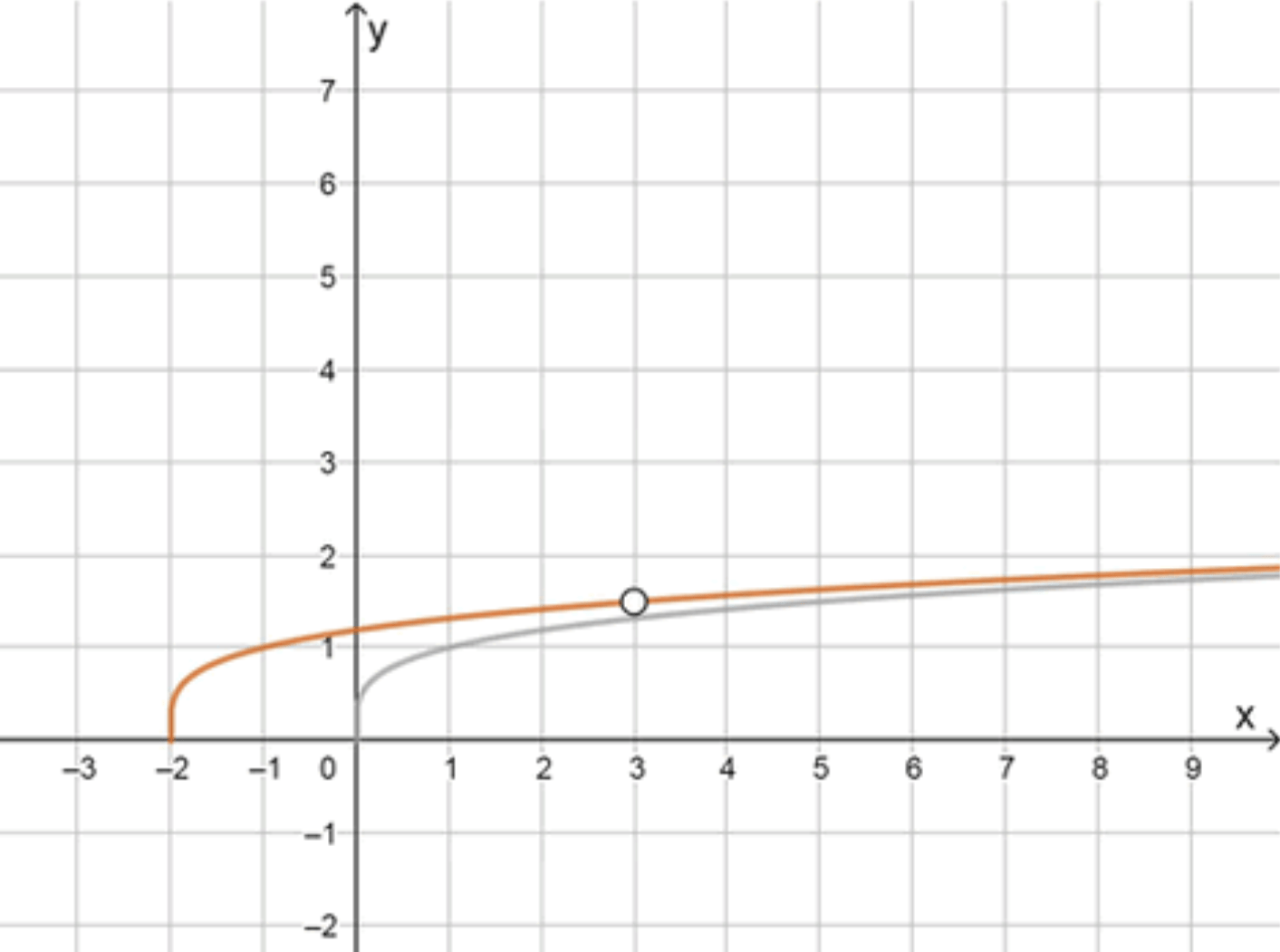
• Это график функции $y = \sqrt[4]{x + 2}$, с начальной точкой в $x = -2$, но без точки $x = 3$.
• Область определения:

  $$D(y) = [-2; 3) \cup (3; +\infty)$$

• Область значений:
  • Корень четвёртой степени — всегда $\geq 0$
  • При $x = -2 \Rightarrow y = \sqrt[4]{0} = 0$
  • При $x \to +\infty \Rightarrow y \to +\infty$

  $$E(y) = [0; +\infty)$$

• В точке $x = 3$ — удалённая точка, из-за нуля в знаменателе исходного выражения.

Вывод:

График функции — это график $y = \sqrt[4]{x + 2}$, начиная с точки $x = -2$, но с выколотой точкой при $x = 3$.
На графике будет разрыв в этой точке.