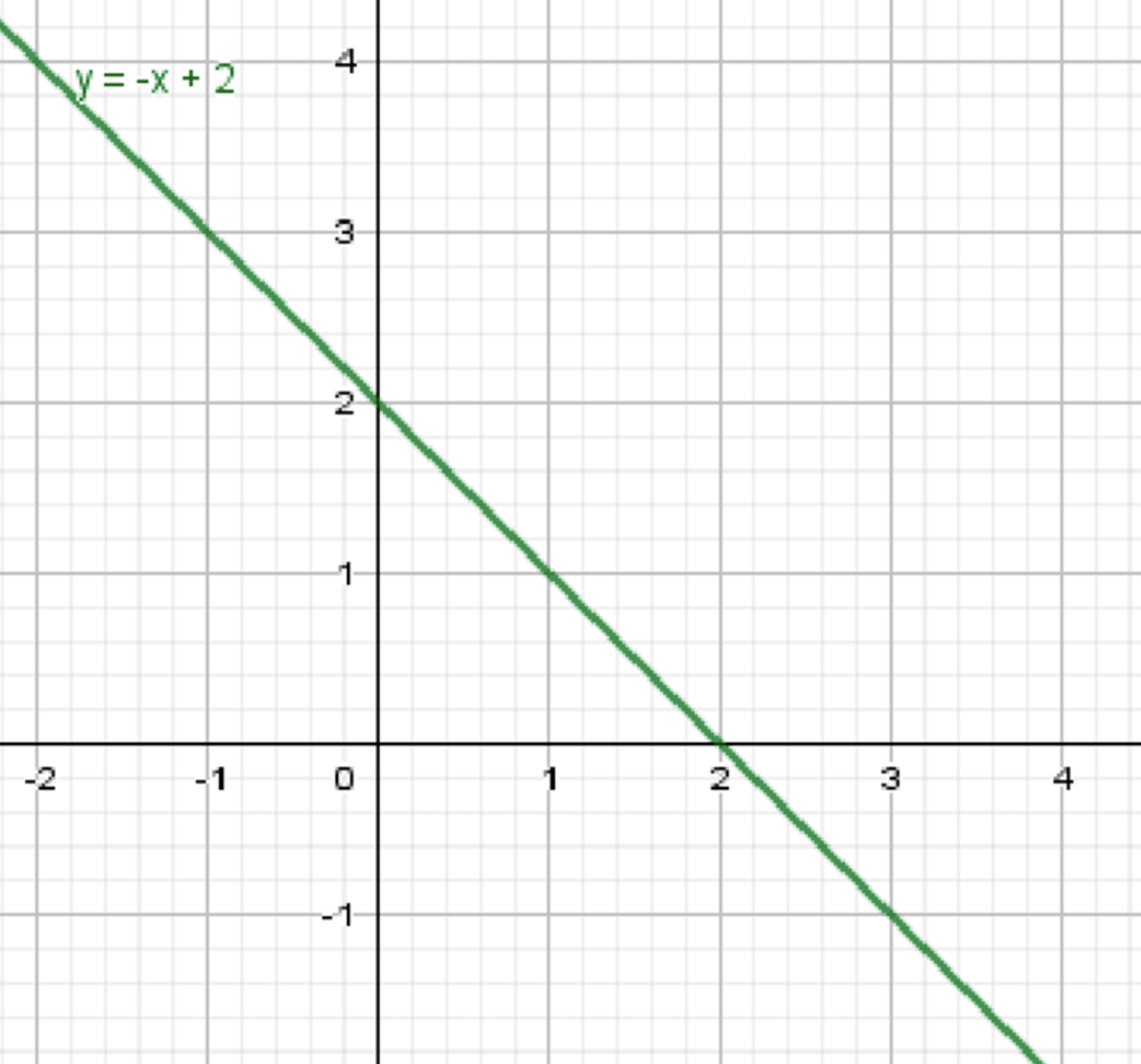ГДЗ 10-11 Класс Номер 35.30 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y=\sqrt[4]{(x-2{)}^4}$

б) $y=\sqrt[5]{(2-x{)}^5}$

в) $y=\sqrt[3]{(x+1{)}^3}$

г) $y=\sqrt[6]{(3-x{)}^6}$

Построить график функции:

а) $y = \sqrt[4]{(x — 2)^4} = |x — 2|$;
Если $x \geq 2$, тогда:

$$y = x — 2$$

Если $x < 2$, тогда:

$$y = 2 — x$$

График функции:

б) $y = \sqrt[5]{(2 — x)^5} = 2 — x$;
График функции:

в) $y = \sqrt[3]{(x + 1)^3} = x + 1$;
График функции:

г) $y = \sqrt[6]{(3 — x)^6} = |3 — x|$;
Если $x \leq 3$, тогда:

$$y = 3 — x$$

Если $x > 3$, тогда:

$$y = x — 3$$

График функции:

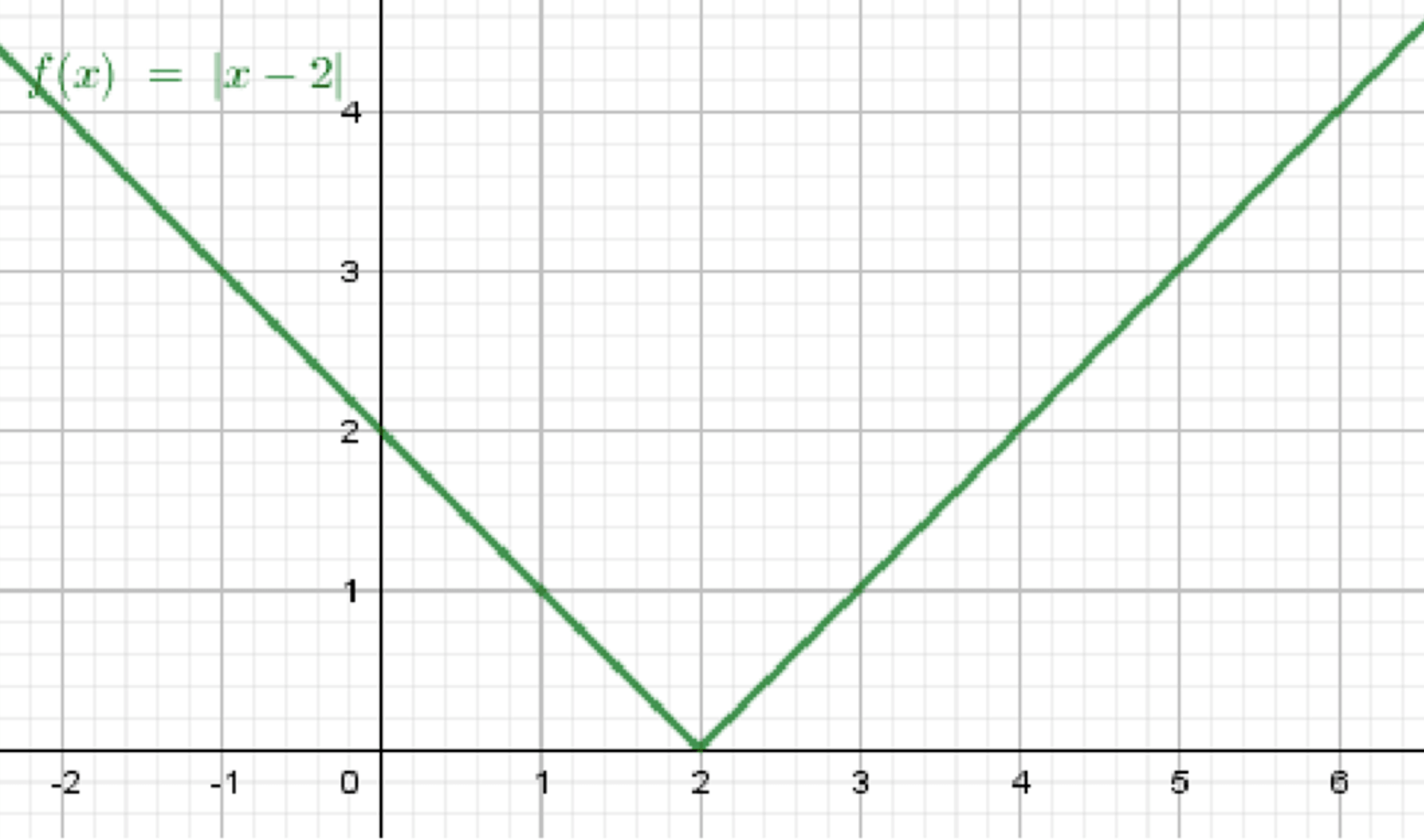
Задача а) $y = \sqrt[4]{(x — 2)^4} = |x — 2|$

Шаг 1: Разбор функции

Исходная функция имеет вид:

$$y = \sqrt[4]{(x — 2)^4}$$

Так как степень $4$ у выражения $(x — 2)^4$ чётная, результат всегда будет неотрицательным, а четвёртый корень из четвёртого степени выражения будет равен абсолютному значению:

$$y = |x — 2|$$

Шаг 2: Разбор на интервалы

Для $x \geq 2$:

$$|x — 2| = x — 2$$

График будет представлять собой прямую с угловым коэффициентом 1, начинающуюся в точке $(2, 0)$, где линия будет возрастать.

Для $x < 2$:

$$|x — 2| = 2 — x$$

График будет представлять собой прямую с угловым коэффициентом -1, начинающуюся в точке $(2, 0)$, и линия будет убывать.

Шаг 3: Описание графика

График функции — это V-образная фигура, вершина которой находится в точке $(2, 0)$. Для значений $x \geq 2$ линия будет возрастать, а для значений $x < 2$ — убывать. Обе ветви графика имеют угловые коэффициенты 1 и -1 соответственно.

Задача б) $y = \sqrt[5]{(2 — x)^5} = 2 — x$

Шаг 1: Разбор функции

Исходная функция:

$$y = \sqrt[5]{(2 — x)^5}$$

Так как степень $5$ нечётная, мы можем упростить выражение, получив:

$$y = 2 — x$$

Шаг 2: Описание графика

Функция $y = 2 — x$ представляет собой прямую линию с угловым коэффициентом -1, которая пересекает ось $y$ в точке $(0, 2)$. График будет наклонён вниз, начиная с точки $(0, 2)$, и будет продолжаться в обе стороны с угловым коэффициентом -1.

Шаг 3: Описание графика

График этой функции — это прямая линия, которая имеет угловой коэффициент -1 и пересекает ось $y$ в точке $(0, 2)$. Линия убывает, поскольку угловой коэффициент отрицателен.

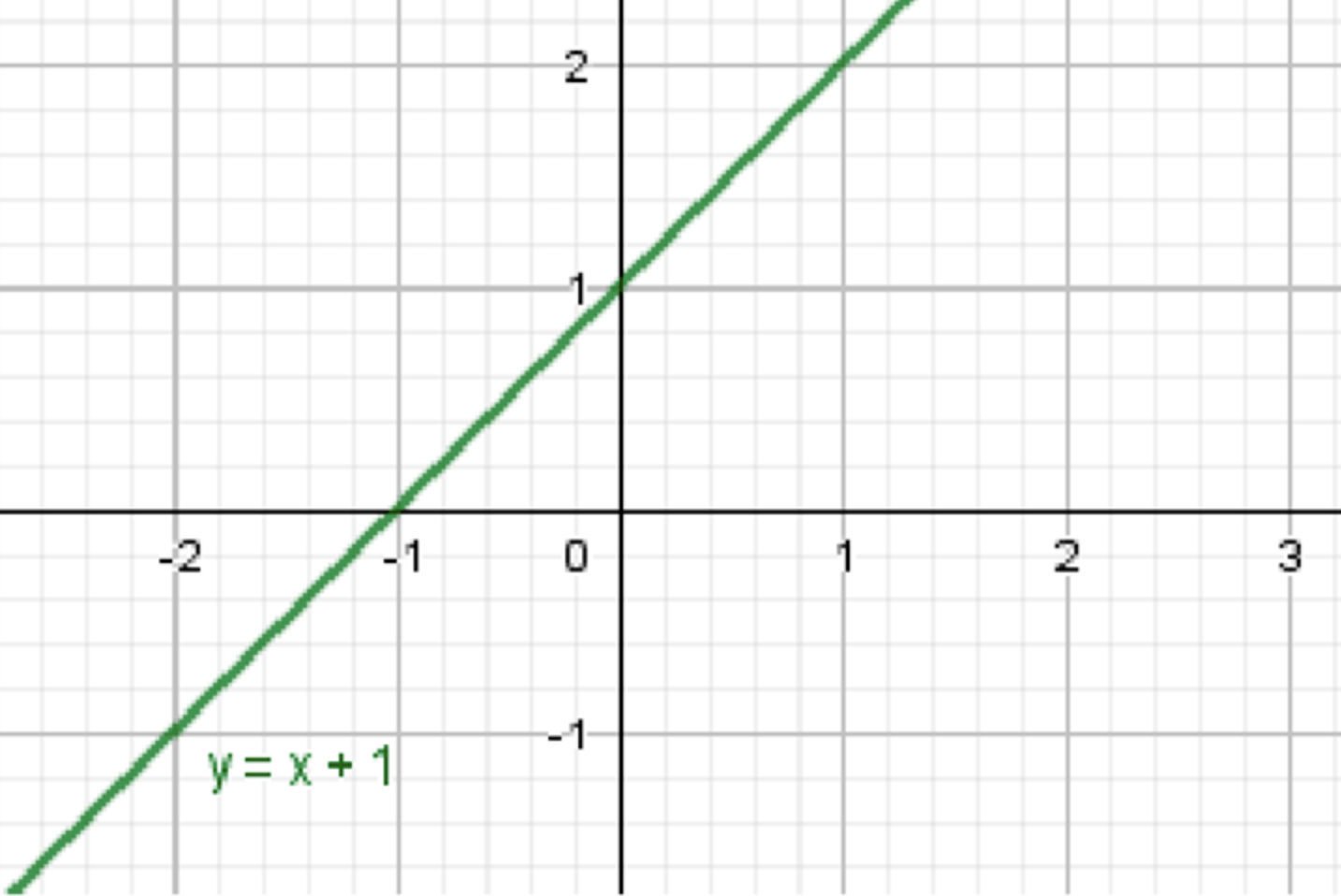
Задача в) $y = \sqrt[3]{(x + 1)^3} = x + 1$

Шаг 1: Разбор функции

Исходная функция:

$$y = \sqrt[3]{(x + 1)^3}$$

Поскольку степень $3$ нечётная, можем упростить выражение, получив:

$$y = x + 1$$

Шаг 2: Описание графика

Это простая линейная функция с угловым коэффициентом 1, которая пересекает ось $y$ в точке $(0, 1)$. График будет представлять собой прямую линию с угловым коэффициентом 1, начинающуюся с точки $(0, 1)$ и продолжающуюся в обе стороны, наклоняясь вверх.

Шаг 3: Описание графика

График этой функции — это прямая линия с угловым коэффициентом 1, пересекающая ось $y$ в точке $(0, 1)$. Линия возрастает, так как угловой коэффициент положительный.

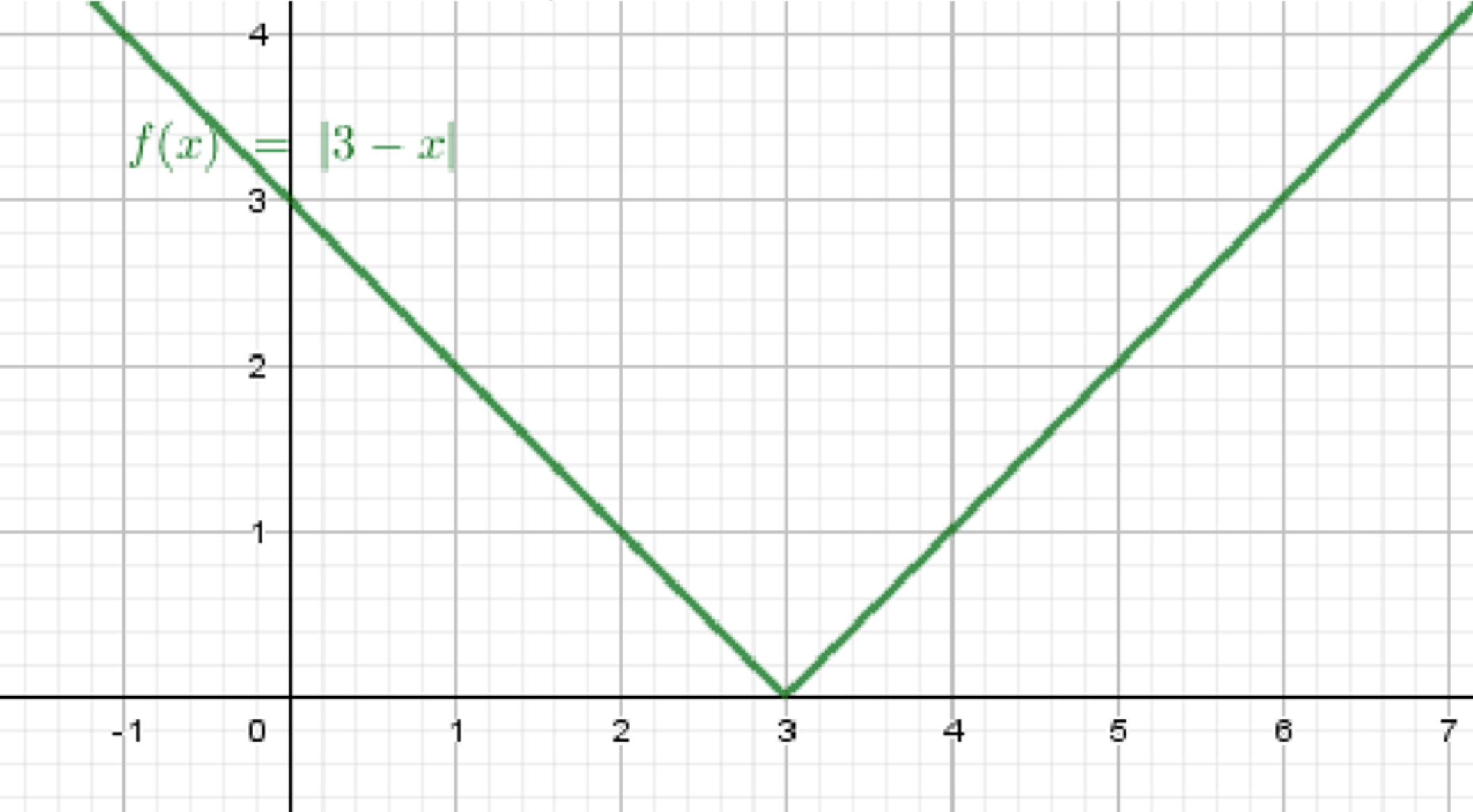
Задача г) $y = \sqrt[6]{(3 — x)^6} = |3 — x|$

Шаг 1: Разбор функции

Исходная функция:

$$y = \sqrt[6]{(3 — x)^6}$$

Так как степень $6$ чётная, результат будет всегда неотрицательным, и мы получаем:

$$y = |3 — x|$$

Шаг 2: Разбор на интервалы

Для $x \leq 3$:

$$|3 — x| = 3 — x$$

График будет представлять собой прямую с угловым коэффициентом -1, начинающуюся в точке $(3, 0)$, и линия будет убывать.

Для $x > 3$:

$$|3 — x| = x — 3$$

График будет представлять собой прямую с угловым коэффициентом 1, начинающуюся в точке $(3, 0)$, и линия будет возрастать.

Шаг 3: Описание графика

График функции — это V-образная фигура, вершина которой находится в точке $(3, 0)$. Для значений $x \leq 3$ линия будет убывать, а для значений $x > 3$ — возрастать. Обе ветви графика имеют угловые коэффициенты -1 и 1 соответственно.