ГДЗ 10-11 Класс Номер 38.1 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y = x^{10}$

б) $y=x^{-3}$

в) $y = x^5$

г) $y=x^{-4}$

Построить график функции:

а) $y = x^{10}$;
Область определения:
$D(y) = (-\infty; +\infty)$;
Функция является четной:
$y(-x) = (-x)^{10} = x^{10} = y(x)$;
Координаты некоторых точек:

График функции:

б) $y = x^{-3} = \frac{1}{x^3}$;
Область определения:
$D(y) = (-\infty; 0) \cup (0; +\infty)$;
Функция является нечетной:
$y(-x) = (-x)^{-3} = -x^{-3} = -y(x)$;
Координаты некоторых точек:

График функции:

в) $y = x^5$;
Область определения:
$D(y) = (-\infty; +\infty)$;
Функция является нечетной:
$y(-x) = (-x)^5 = -x^5 = -y(x)$;
Координаты некоторых точек:

График функции:

г) $y = x^{-4} = \frac{1}{x^4}$;
Область определения:
$D(y) = (-\infty; 0) \cup (0; +\infty)$;
Функция является четной:
$y(-x) = (-x)^{-4} = x^{-4} = y(x)$;
Координаты некоторых точек:

График функции:

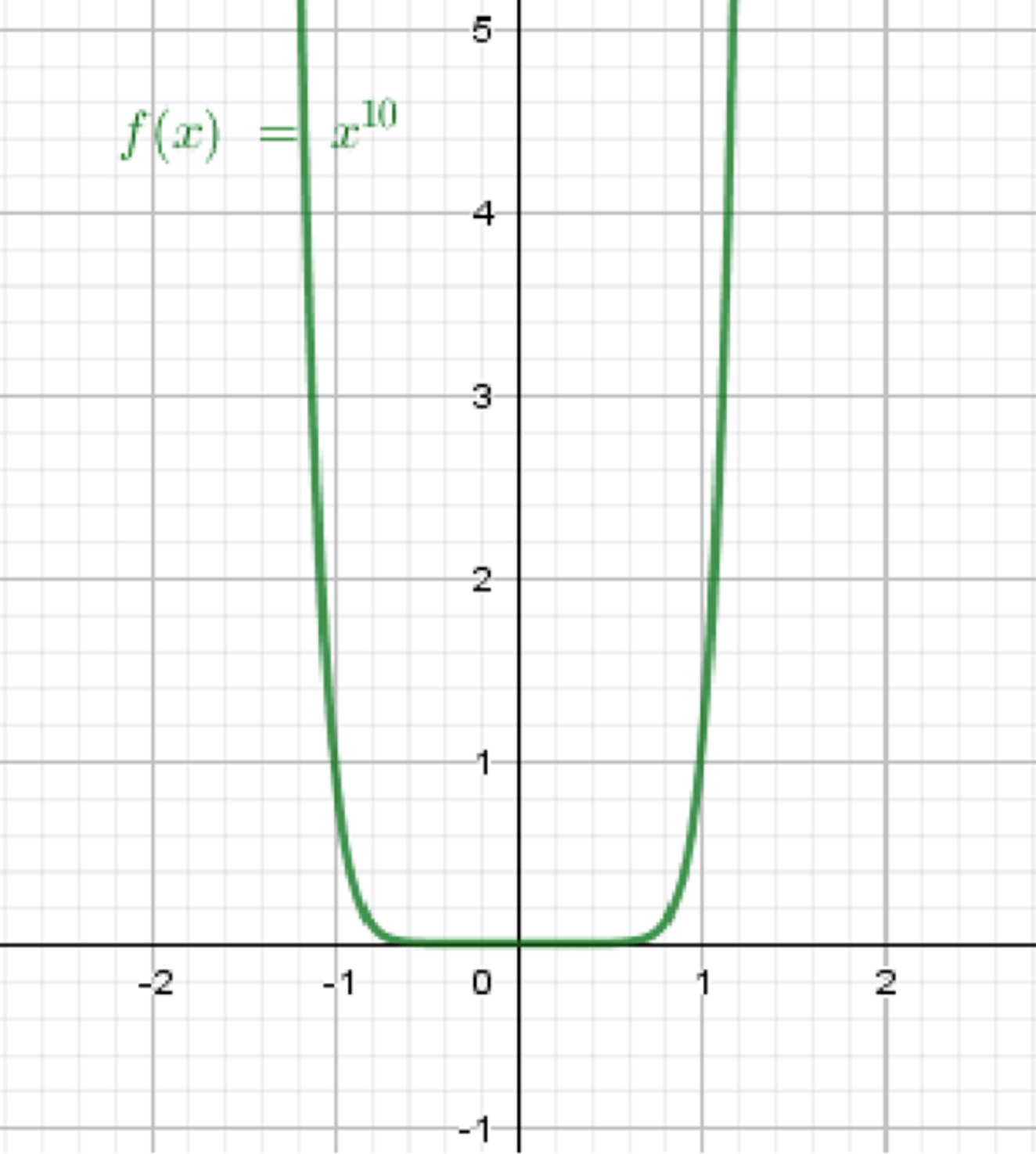
а) $y = x^{10}$

1. Область определения

Функция $y = x^{10}$ — это степенная функция с положительным чётным показателем.
Такая функция определена при любом действительном значении $x$.

Вывод:

$$D(y) = (-\infty; +\infty)$$

2. Чётность функции

Проверим, как функция ведёт себя при замене $x$ на $-x$:

$$y(-x) = (-x)^{10} = x^{10} = y(x)$$

Вывод:
Функция является чётной, так как $y(-x) = y(x)$.
Следствие: график симметричен относительно оси $Oy$.

3. Таблица значений

Вычислим значения функции при некоторых значениях $x$:

$$\begin{align*} x = 0 &\Rightarrow y = 0^{10} = 0 \\ x = 1 &\Rightarrow y = 1^{10} = 1 \\ x = 2 &\Rightarrow y = 2^{10} = 1024 \\ \end{align*}$$

Таблица:

4. Поведение графика

• При $x > 0$: $y$ резко возрастает.
• При $x < 0$: поведение такое же, как при положительном $x$, так как функция чётная.
• При $x = 0$: $y = 0$
• При $x \to \pm\infty$: $y \to +\infty$

График:
Проходит через точку (0, 0), обе ветви поднимаются вверх, симметричны относительно оси $Oy$.

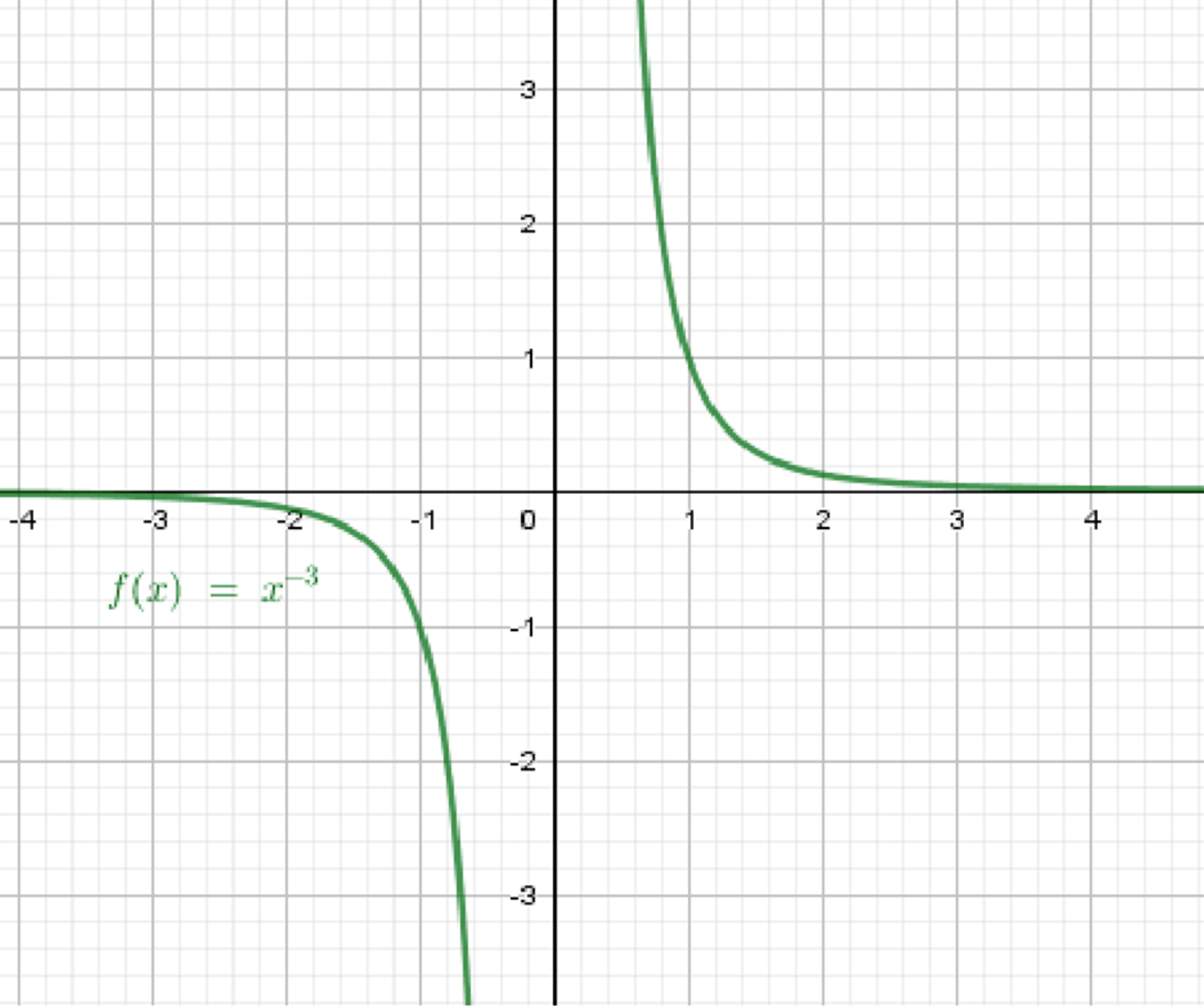
б) $y = x^{-3} = \frac{1}{x^3}$

1. Область определения

Функция не определена при $x = 0$, так как деление на ноль невозможно.

Вывод:

$$D(y) = (-\infty; 0) \cup (0; +\infty)$$

2. Нечётность функции

Проверим:

$$y(-x) = (-x)^{-3} = -x^{-3} = -y(x)$$

Вывод:
Функция нечётная, поскольку $y(-x) = -y(x)$.
Следствие: график симметричен относительно начала координат.

3. Таблица значений

$$\begin{align*} x = 0.5 &\Rightarrow y = \frac{1}{(0.5)^3} = \frac{1}{0.125} = 8 \\ x = 1 &\Rightarrow y = \frac{1}{1} = 1 \\ x = 2 &\Rightarrow y = \frac{1}{8} = 0.125 \\ \end{align*}$$

Таблица:

4. Поведение графика

• При $x \to 0^+$: $y \to +\infty$
• При $x \to 0^-$: $y \to -\infty$
• При $x \to +\infty$: $y \to 0^+$
• При $x \to -\infty$: $y \to 0^-$

График:
Состоит из двух ветвей в первой и третьей четвертях, стремится к бесконечности при приближении к нулю, и к нулю при удалении от него.

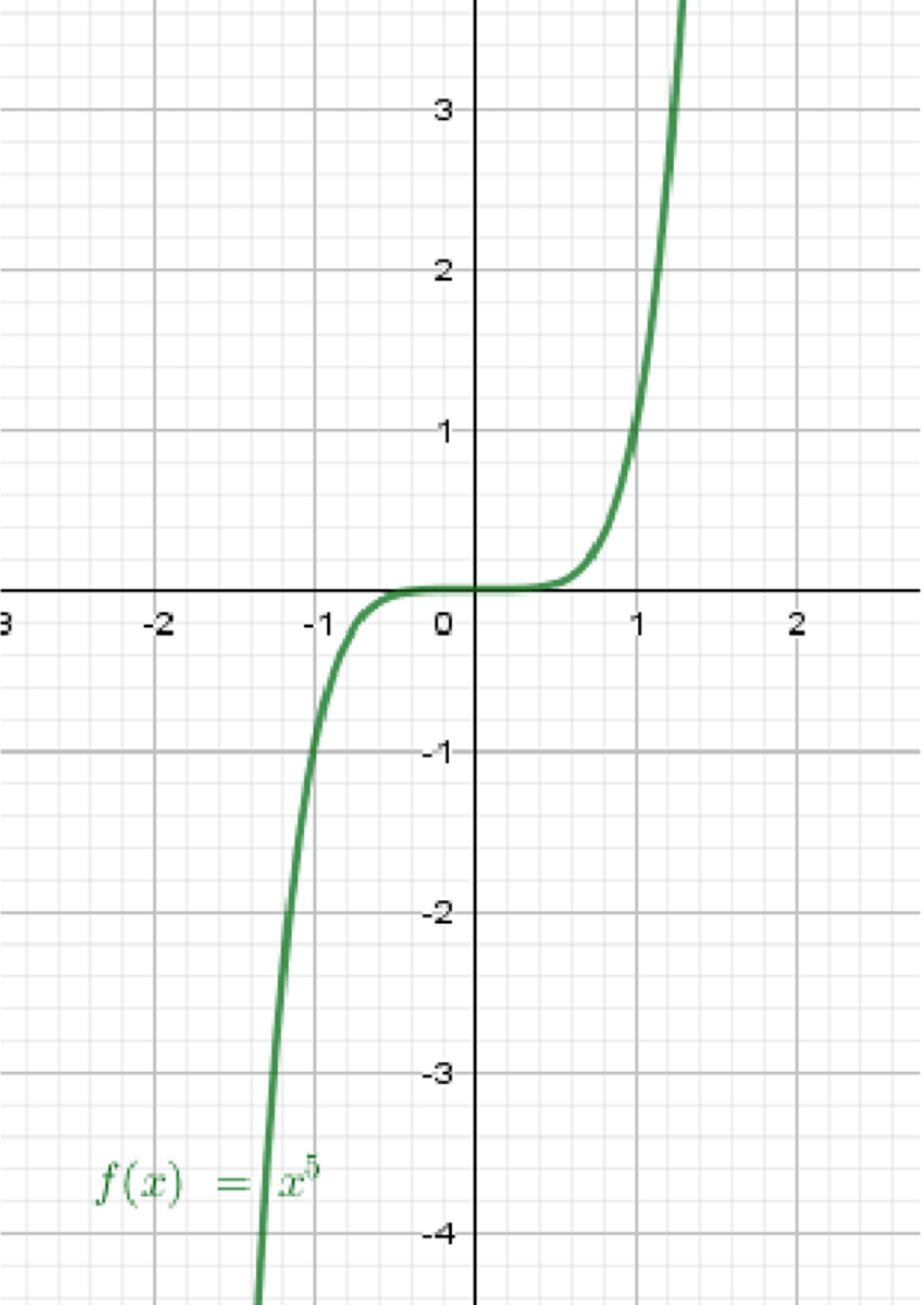
в) $y = x^5$

1. Область определения

Функция определена для всех действительных значений $x$.

Вывод:

$$D(y) = (-\infty; +\infty)$$

2. Нечётность функции

$$y(-x) = (-x)^5 = -x^5 = -y(x)$$

Вывод:
Функция нечётная, график симметричен относительно начала координат.

3. Таблица значений

$$\begin{align*} x = 0 &\Rightarrow y = 0^5 = 0 \\ x = 1 &\Rightarrow y = 1^5 = 1 \\ x = 2 &\Rightarrow y = 2^5 = 32 \\ \end{align*}$$

Таблица:

4. Поведение графика

• Монотонно возрастает на всей области определения
• При $x \to -\infty$: $y \to -\infty$
• При $x \to +\infty$: $y \to +\infty$

График:
Проходит через начало координат, симметричен относительно него, растёт как слева, так и справа.

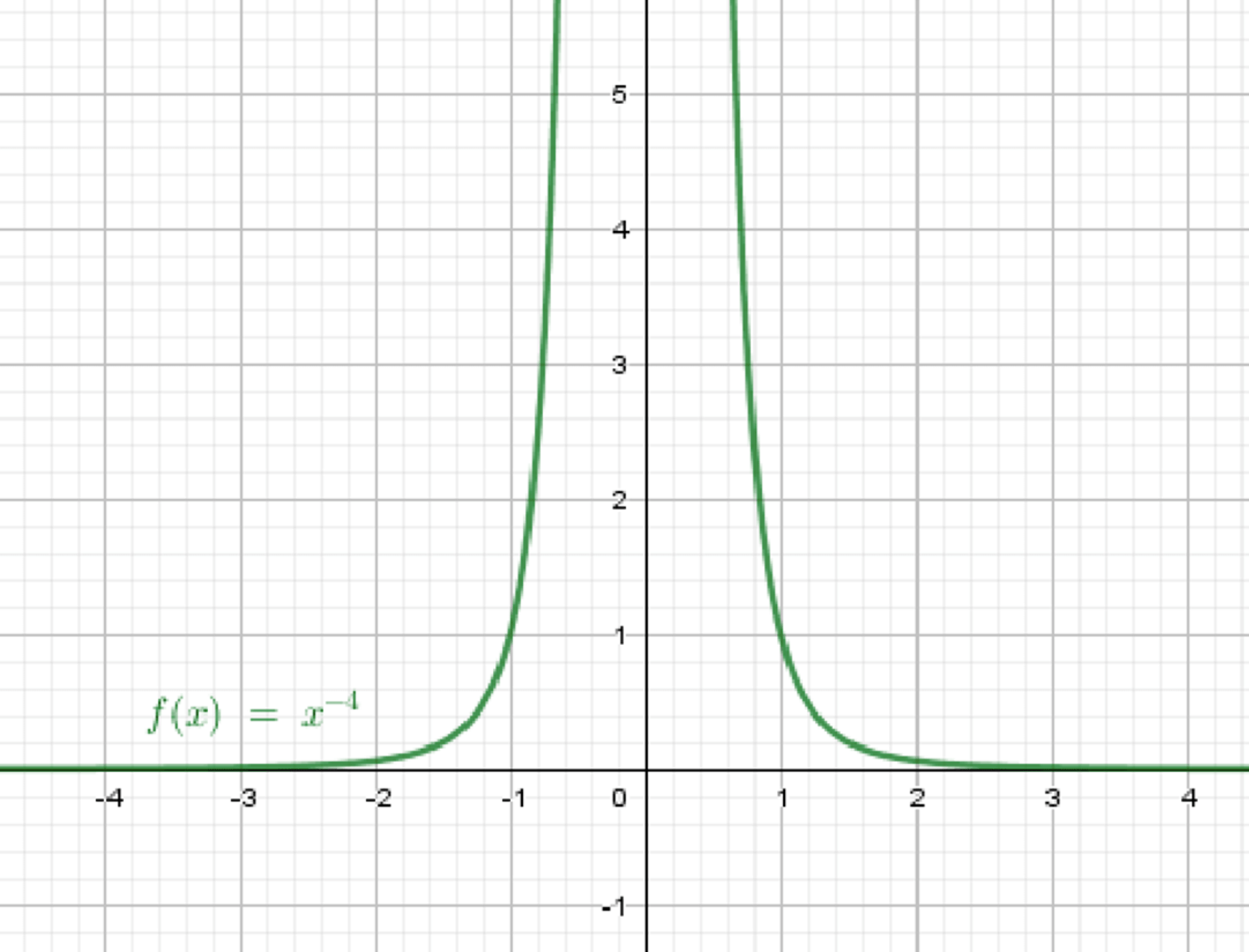
г) $y = x^{-4} = \frac{1}{x^4}$

1. Область определения

Знаменатель $x^4$ не должен быть равен нулю.

Вывод:

$$D(y) = (-\infty; 0) \cup (0; +\infty)$$

2. Чётность функции

$$y(-x) = (-x)^{-4} = \frac{1}{x^4} = y(x)$$

Вывод:
Функция чётная, график симметричен относительно оси $Oy$.

3. Таблица значений

$$\begin{align*} x = 0.5 &\Rightarrow y = \frac{1}{(0.5)^4} = \frac{1}{0.0625} = 16 \\ x = 1 &\Rightarrow y = \frac{1}{1^4} = 1 \\ x = 2 &\Rightarrow y = \frac{1}{16} = 0.0625 \\ \end{align*}$$

Таблица:

4. Поведение графика

• При $x \to 0^\pm$: $y \to +\infty$
• При $x \to \pm\infty$: $y \to 0^+$

График:
Две ветви в первой и второй четвертях, обе находятся выше оси $Ox$, стремятся к бесконечности при приближении к нулю, и к нулю при удалении от него.