ГДЗ 10-11 Класс Номер 38.12 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Постройте график функции:

а) $y = (x + 2)^{\frac{1}{2}}$;

б) $y = x^{\frac{7}{2}} — 3$;

в) $y = (x — 1)^{-\frac{2}{3}}$;

г) $y = x^{-\frac{1}{3}} + 4$

Построить график функции:

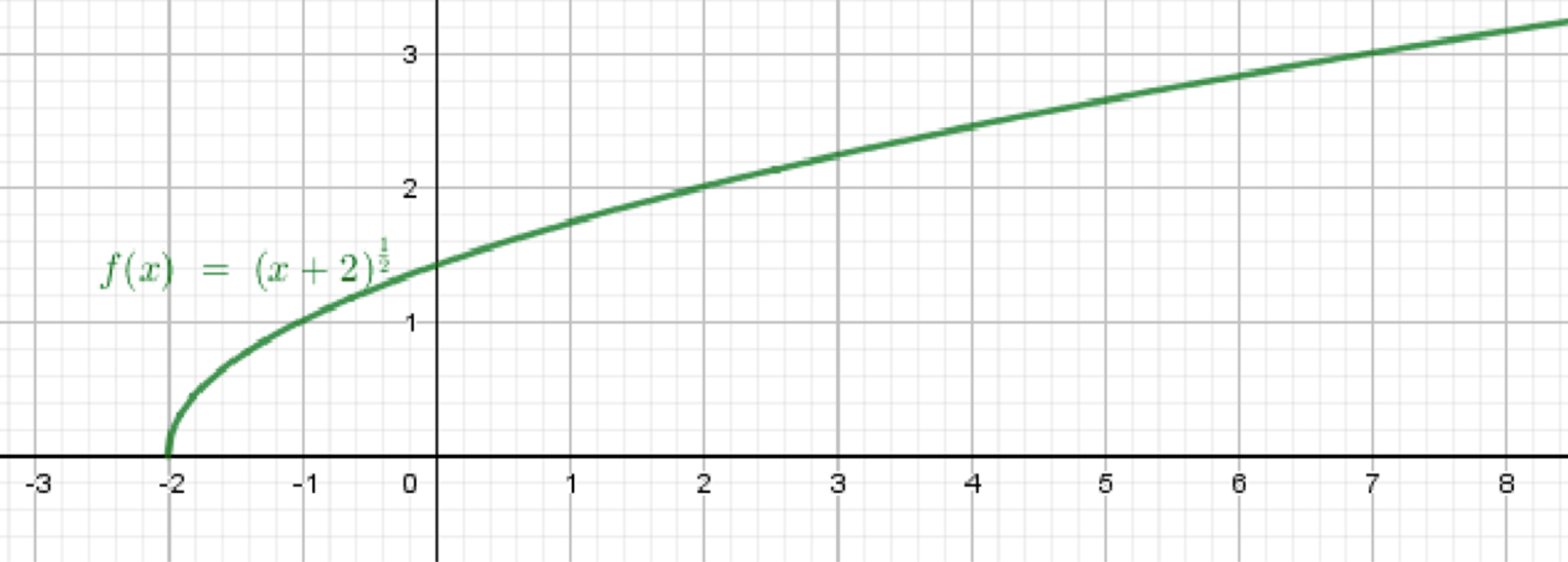
а) $y = (x + 2)^{\frac{1}{2}}$;
Построим график функции $y = x^{\frac{1}{2}}$;
Переместим его на 2 единицы влево:

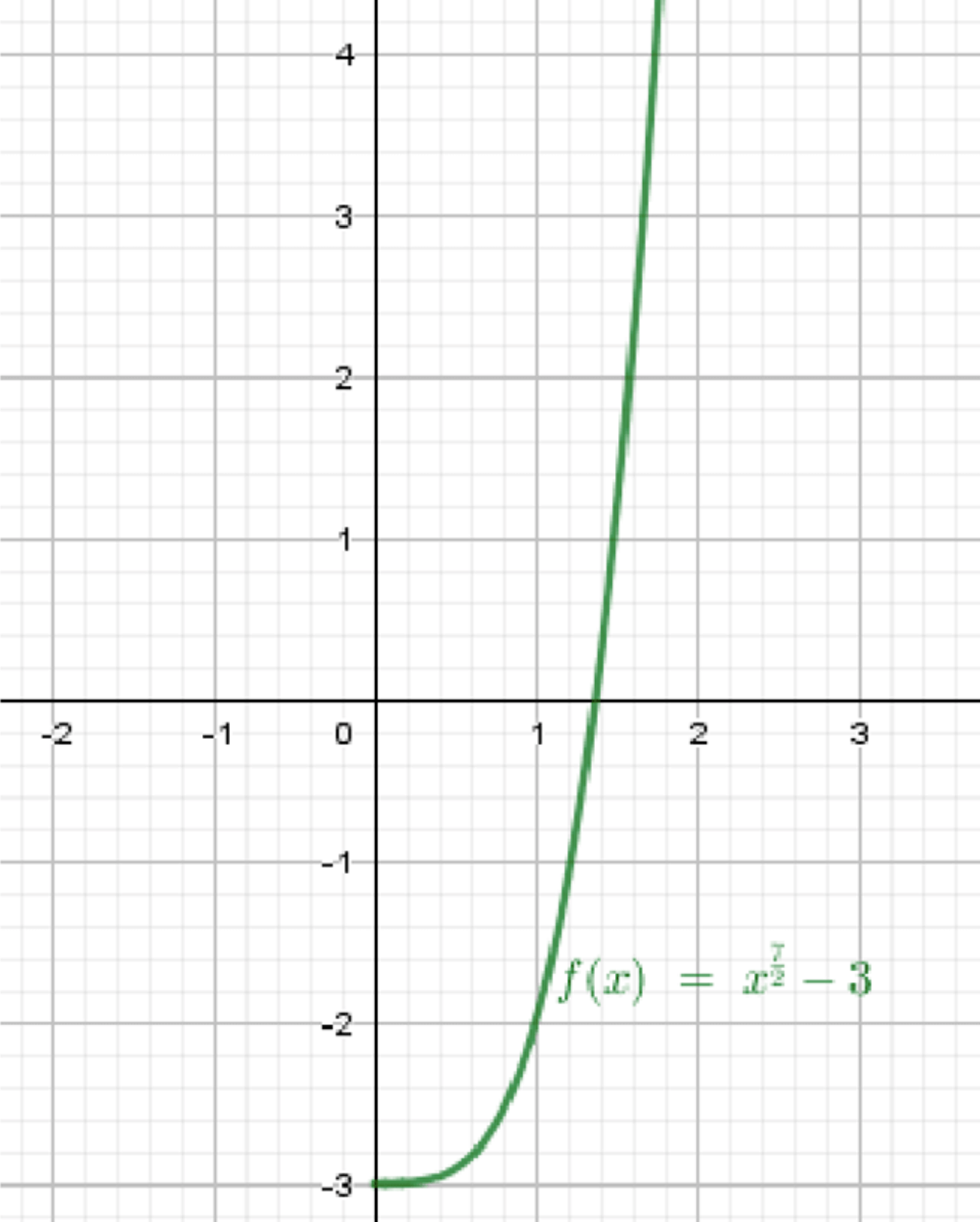
б) $y = x^{\frac{7}{2}} — 3$;
Построим график функции $y = x^{\frac{7}{2}}$;
Переместим его на 3 единицы вниз:

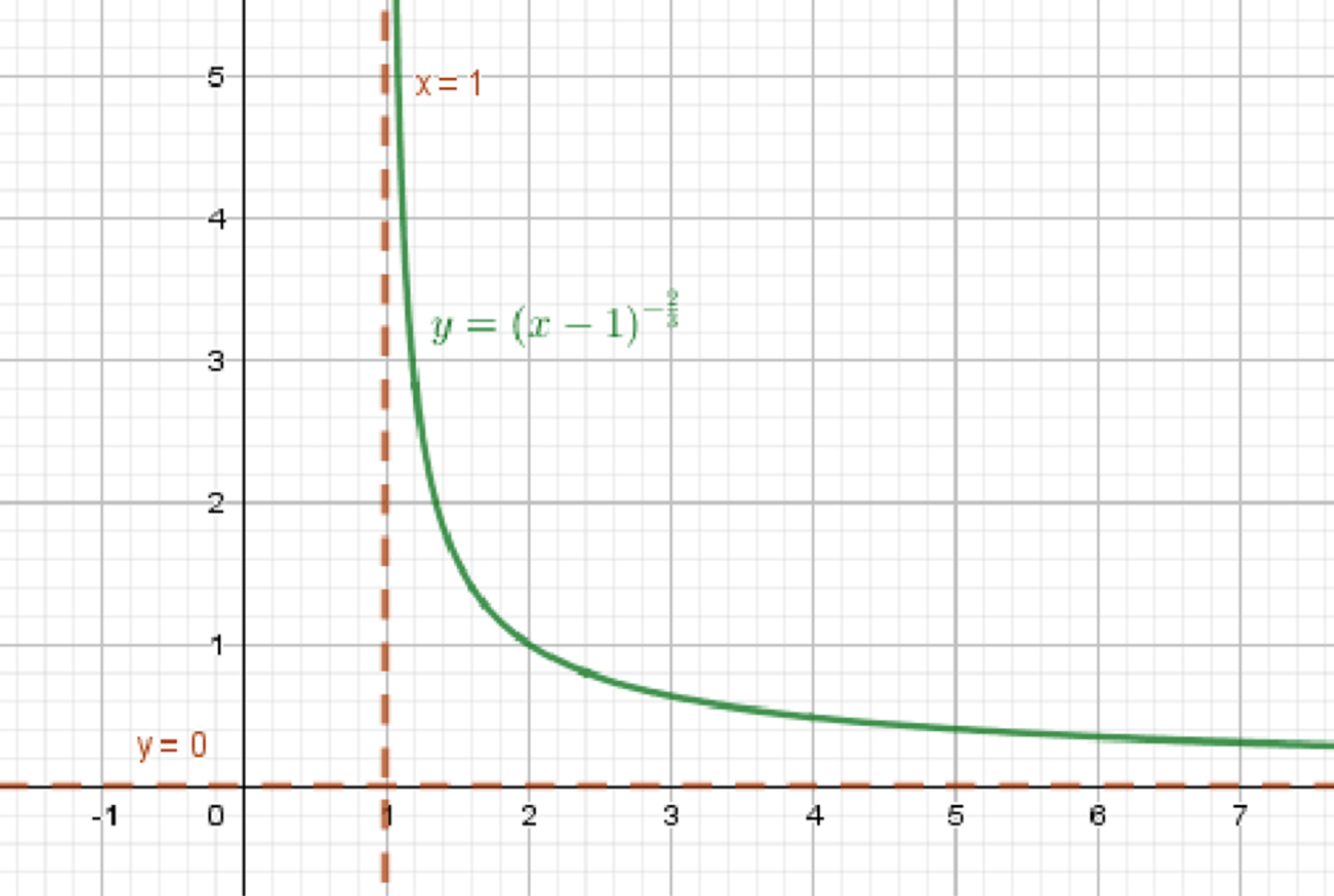
в) $y = (x — 1)^{-\frac{2}{3}}$;
Построим график функции $y = x^{-\frac{2}{3}}$;
Переместим его на 1 единицу вправо:

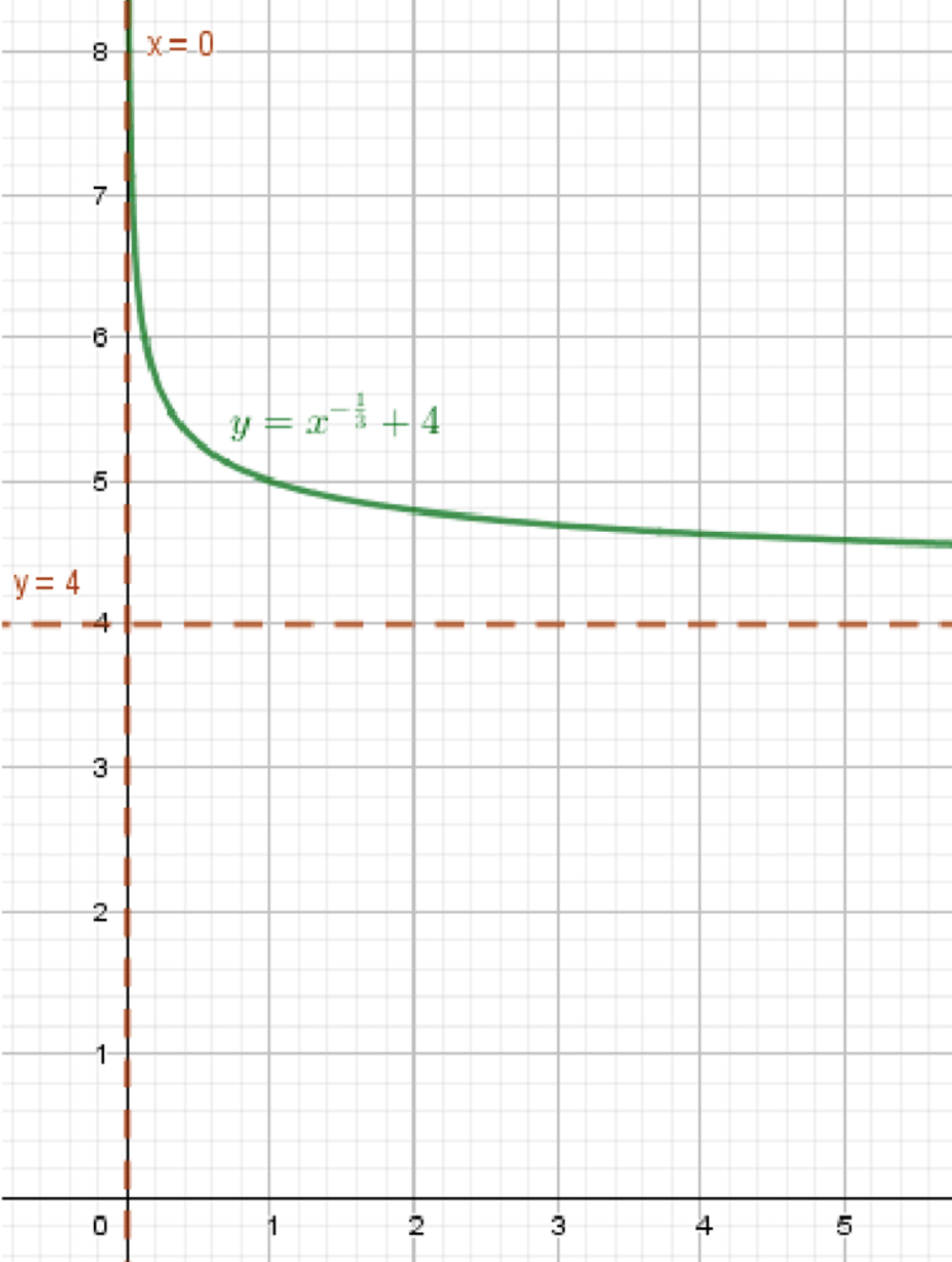
г) $y = x^{-\frac{1}{3}} + 4$;
Построим график функции $y = x^{-\frac{1}{3}}$;
Переместим его на 4 единицы вверх:

а) $y = (x + 2)^{\frac{1}{2}}$

1. Базовая функция

Начнём с функции:

$$y = x^{\frac{1}{2}} = \sqrt{x}$$

Свойства графика:

• Область определения: $x \geq 0$
• Значения $y$ неотрицательны: $y \geq 0$
• График — плавная возрастающая кривая, начинающаяся в точке $(0; 0)$ и идущая вправо и вверх.
• Примеры точек:
  $(0; 0),\ (1; 1),\ (4; 2),\ (9; 3)$

2. Преобразование

В функции $y = (x + 2)^{\frac{1}{2}}$, к аргументу прибавлено 2.

Что это значит?

• $x$ заменили на $x + 2$
• Это соответствует сдвигу графика влево на 2 единицы

3. Итоговое описание графика

• График начинается в точке $x = -2$, потому что:

  $$x + 2 \geq 0 \Rightarrow x \geq -2$$

• Новая начальная точка: $(-2; 0)$
• Кривая идёт вправо и вверх, как у обычной функции $\sqrt{x}$, но вся «перенесена» влево на 2 единицы

б) $y = x^{\frac{7}{2}} — 3$

1. Базовая функция

Исходная функция:

$$y = x^{\frac{7}{2}} = \sqrt{x^7}$$

Свойства:

• Область определения: $x \geq 0$
• Функция строго возрастает
• График проходит через точки:

  $$(0; 0),\ (1; 1),\ (4; 128)$$

• Значения $y$ возрастают очень быстро

2. Преобразование

Вся функция уменьшена на 3:

$$y = x^{\frac{7}{2}} — 3$$

Это вертикальный сдвиг вниз на 3 единицы.

3. Итоговое описание графика

• Область определения: $x \geq 0$
• График начинается в точке $(0; -3)$
• Кривая поднимается вверх от этой точки, стремительно увеличиваясь
• По форме повторяет график $x^{\frac{7}{2}}$, но сдвинута вниз

в) $y = (x — 1)^{-\frac{2}{3}}$

1. Базовая функция

Исходная функция:

$$y = x^{-\frac{2}{3}} = \frac{1}{\sqrt[3]{x^2}}$$

Свойства:

• Область определения: $x \in \mathbb{R} \setminus \{0\}$
• Значения всегда положительны
• Симметрия: чётная функция, график симметричен относительно оси $Oy$
• Поведение:
  • При $x \to 0^\pm$: $y \to +\infty$
  • При $|x| \to \infty$: $y \to 0$
• Примеры точек:
  $x = \pm1 \Rightarrow y = 1$,
  $x = \pm8 \Rightarrow y = \frac{1}{4}$

2. Преобразование

Функция становится:

$$y = (x — 1)^{-\frac{2}{3}}$$

Заменили $x$ на $x — 1$ → сдвиг вправо на 1 единицу

3. Итоговое описание графика

• Область определения:

  $$x — 1 \neq 0 \Rightarrow x \neq 1$$

• График симметричен относительно вертикальной прямой $x = 1$
• На этой прямой — вертикальная асимптота
• По форме — две ветви:
  • Слева от $x = 1$: убывает к асимптоте
  • Справа от $x = 1$: убывает от асимптоты

г) $y = x^{-\frac{1}{3}} + 4$

1. Базовая функция

Функция:

$$y = x^{-\frac{1}{3}} = \frac{1}{\sqrt[3]{x}}$$

Свойства:

• Область определения: $x \ne 0$
• Значения: могут быть как положительные, так и отрицательные
• Симметрия: нечётная функция (график симметричен относительно начала координат)
• Поведение:
  • При $x \to 0^+$: $y \to +\infty$
  • При $x \to 0^-$: $y \to -\infty$
  • При $x \to \pm\infty$: $y \to 0$

Примеры точек:
$x = 1 \Rightarrow y = 1$,
$x = -1 \Rightarrow y = -1$,
$x = 8 \Rightarrow y = \frac{1}{2}$

2. Преобразование

$$y = x^{-\frac{1}{3}} + 4$$

Вертикальный сдвиг вверх на 4 единицы

3. Итоговое описание графика

• Область определения: $x \ne 0$
• График стал выше на 4 единицы
• Поведение:
  • При $x \to 0^+$: $y \to +\infty$
  • При $x \to 0^-$: $y \to -\infty$
  • При $x \to \pm\infty$: $y \to 4$ (горизонтальная асимптота)