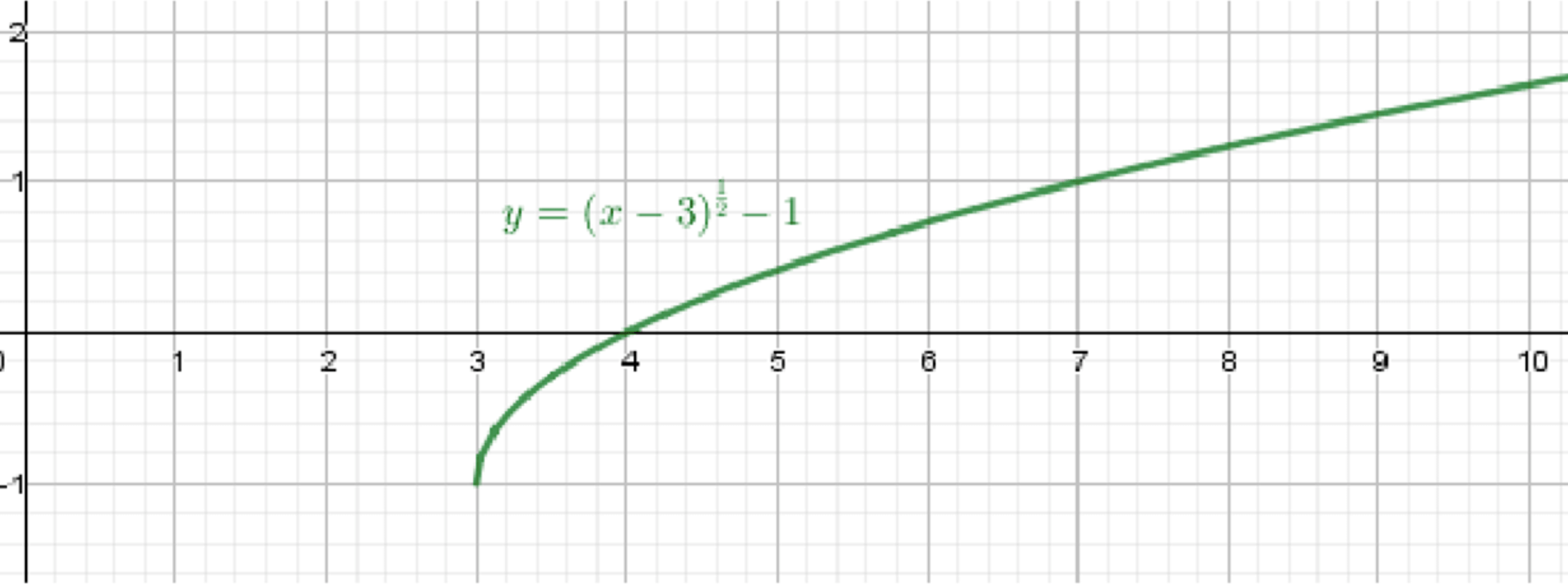ГДЗ 10-11 Класс Номер 38.13 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

а) $y = (x + 3)^{\frac{1}{6}} — 1$;

б) $y = (x — 2)^{-\frac{1}{9}} + 5$;

в) $y = (x + 6)^{\frac{7}{4}} + 2$;

г) $y = (x — 3)^{\frac{1}{2}} — 1$

Построить график функции:

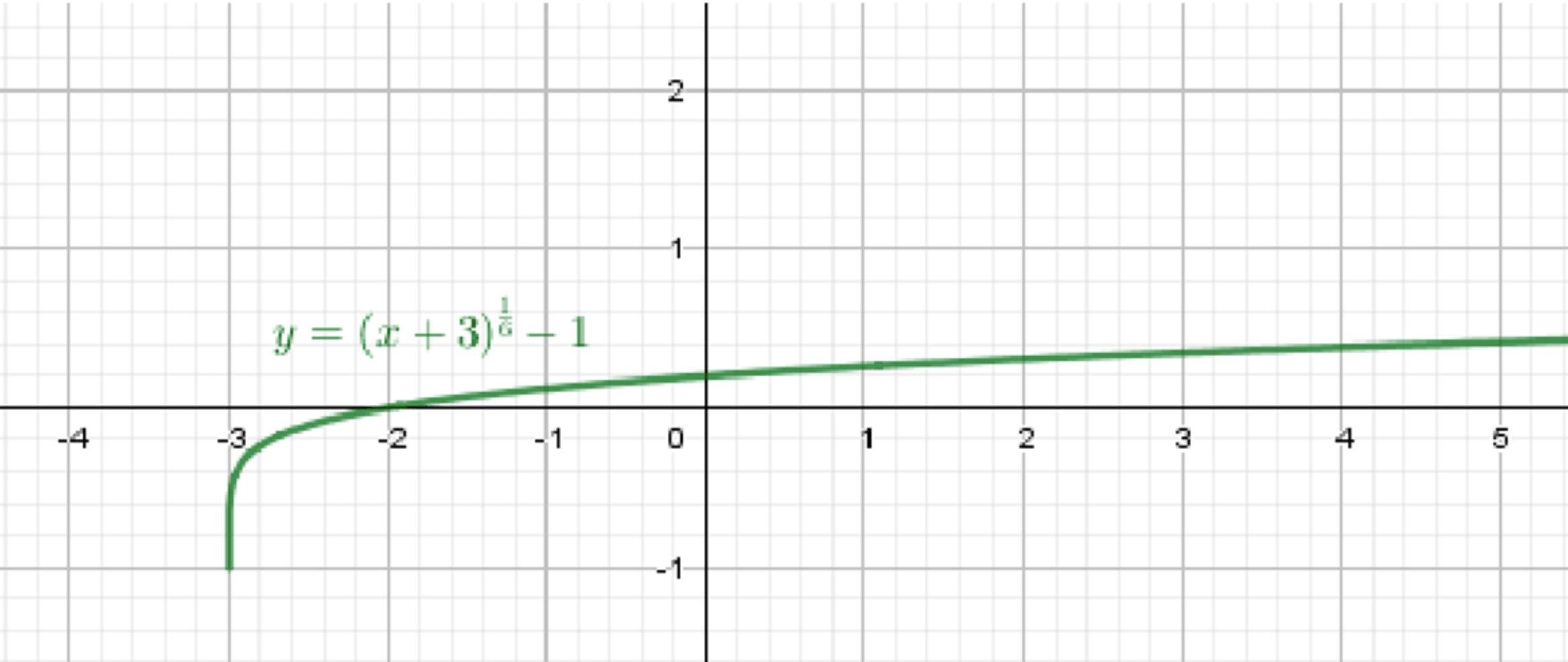
а) $y = (x + 3)^{\frac{1}{6}} — 1$;
Построим график функции $y = x^{\frac{1}{6}}$;
Переместим его на 3 единицы влево;
Переместим его на 1 единицу вниз:

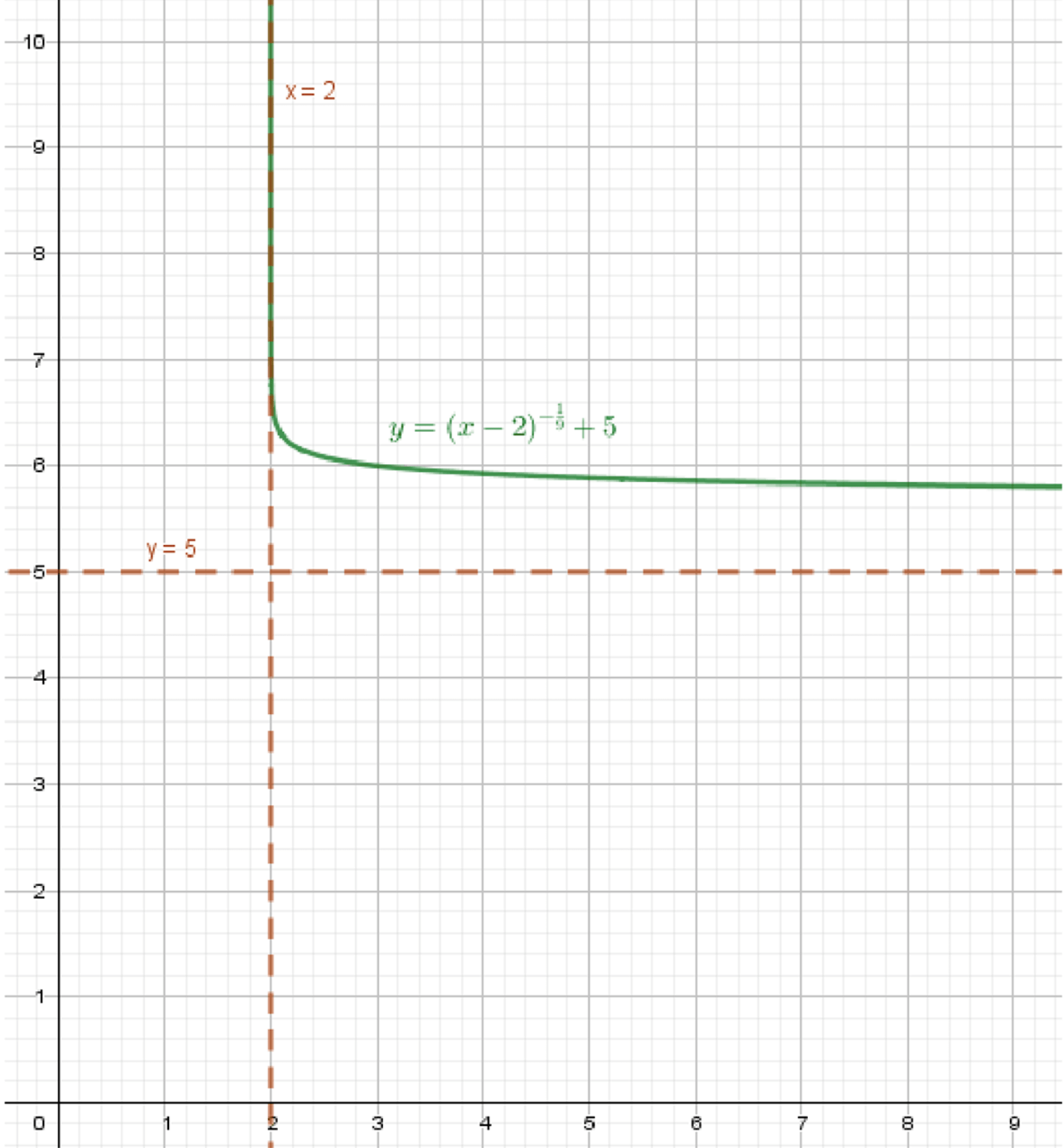
б) $y = (x — 2)^{-\frac{1}{9}} + 5$;
Построим график функции $y = x^{-\frac{1}{9}}$;
Переместим его на 2 единицы вправо;
Переместим его на 5 единиц вверх:

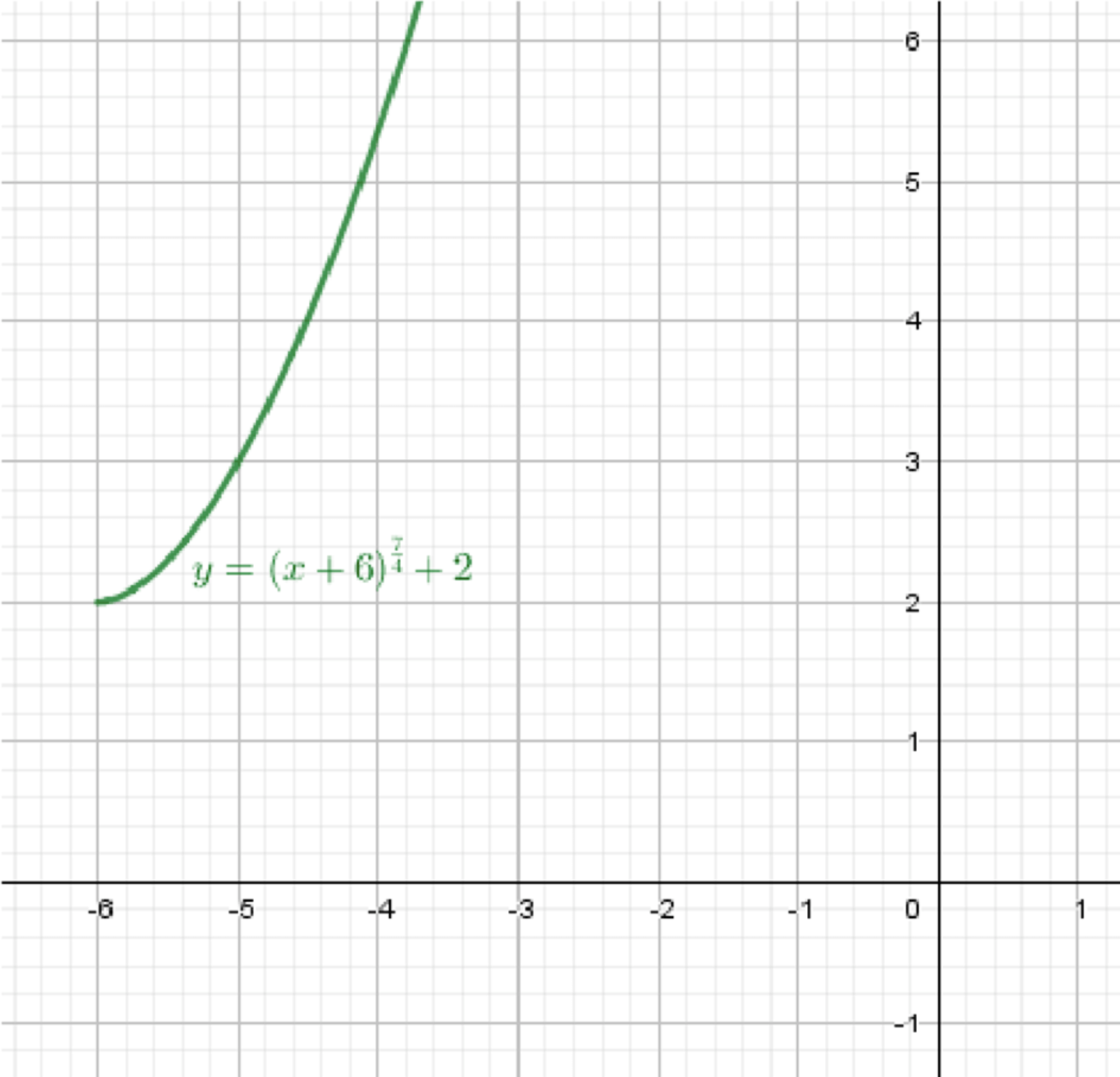
в) $y = (x + 6)^{\frac{7}{4}} + 2$;
Построим график функции $y = x^{\frac{7}{4}}$;
Переместим его на 6 единиц влево;
Переместим его на 2 единицы вверх:

г) $y = (x — 3)^{\frac{1}{2}} — 1$;
Построим график функции $y = x^{\frac{1}{2}}$;
Переместим его на 3 единицы вправо;
Переместим его на 1 единицу вниз:

а) $y = (x + 3)^{\frac{1}{6}} — 1$

Шаг 1: Базовая функция

Функция $y = x^{\frac{1}{6}}$ — это корень шестой степени из $x$.

• Область определения: $x \geq 0$
• Функция возрастает, но очень медленно
• Значения функции положительны
• Примеры точек:
  • $x = 0 \Rightarrow y = 0$
  • $x = 1 \Rightarrow y = 1$
  • $x = 64 \Rightarrow y = 2$

Шаг 2: Горизонтальный сдвиг

Функция становится $y = (x + 3)^{\frac{1}{6}}$

• Это сдвиг графика влево на 3 единицы
• Область определения теперь:

  $$x + 3 \geq 0 \Rightarrow x \geq -3$$

• Начальная точка становится $(-3; 0)$

Шаг 3: Вертикальный сдвиг

Теперь $y = (x + 3)^{\frac{1}{6}} — 1$

• Это сдвиг вниз на 1 единицу
• Начальная точка: $(-3; -1)$

Итоговое описание

• График начинается в точке $(-3; -1)$
• Кривая плавно возрастает вправо
• Имеет форму медленно растущего корня
• Область определения: $x \geq -3$

б) $y = (x — 2)^{-\frac{1}{9}} + 5$

Шаг 1: Базовая функция

Функция $y = x^{-\frac{1}{9}}$

• Это обратная степенная функция
• Значение отрицательной дробной степени:

  $$y = \frac{1}{x^{1/9}} = \frac{1}{\sqrt[9]{x}}$$

• Определена при $x > 0$
• Монотонно убывает
• Значения положительные
• Примеры точек:
  • $x = 1 \Rightarrow y = 1$
  • $x = 512 \Rightarrow y \approx 0.5$

Шаг 2: Горизонтальный сдвиг

$y = (x — 2)^{-\frac{1}{9}}$

• Сдвиг графика вправо на 2 единицы
• Новая область определения:

  $$x — 2 > 0 \Rightarrow x > 2$$

Шаг 3: Вертикальный сдвиг

$y = (x — 2)^{-\frac{1}{9}} + 5$

• Это сдвиг вверх на 5 единиц
• Значения функции теперь находятся выше на 5

Итоговое описание

• Область определения: $x > 2$
• График расположен выше, начинается чуть правее точки $x = 2$
• Убывает вправо, асимптотически приближаясь к $y = 5$

в) $y = (x + 6)^{\frac{7}{4}} + 2$

Шаг 1: Базовая функция

Функция $y = x^{\frac{7}{4}}$

• Показатель больше 1 → быстро возрастающая
• Определена при $x \geq 0$
• Примеры точек:
  • $x = 0 \Rightarrow y = 0$
  • $x = 1 \Rightarrow y = 1$
  • $x = 2 \Rightarrow y \approx 5.66$

Шаг 2: Горизонтальный сдвиг

Функция $y = (x + 6)^{\frac{7}{4}}$

• Это сдвиг влево на 6 единиц
• Новая область определения:

  $$x + 6 \geq 0 \Rightarrow x \geq -6$$

• Начальная точка: $(-6; 0)$

Шаг 3: Вертикальный сдвиг

Функция $y = (x + 6)^{\frac{7}{4}} + 2$

• Это сдвиг вверх на 2 единицы
• Начальная точка: $(-6; 2)$

Итоговое описание

• Область определения: $x \geq -6$
• График начинается в точке $(-6; 2)$, стремительно растёт
• По форме — крутая возрастающая кривая, поднятая вверх на 2

г) $y = (x — 3)^{\frac{1}{2}} — 1$

Шаг 1: Базовая функция

Функция $y = x^{\frac{1}{2}} = \sqrt{x}$

• Область определения: $x \geq 0$
• Монотонно возрастает
• Примеры точек:
  • $x = 0 \Rightarrow y = 0$
  • $x = 1 \Rightarrow y = 1$
  • $x = 4 \Rightarrow y = 2$

Шаг 2: Горизонтальный сдвиг

Функция $y = (x — 3)^{\frac{1}{2}}$

• Сдвиг вправо на 3 единицы
• Новая область определения:

  $$x — 3 \geq 0 \Rightarrow x \geq 3$$

• Начальная точка: $(3; 0)$

Шаг 3: Вертикальный сдвиг

Функция $y = (x — 3)^{\frac{1}{2}} — 1$

• Сдвиг вниз на 1 единицу
• Новая начальная точка: $(3; -1)$

Итоговое описание

• График начинается в точке $(3; -1)$, идёт вправо и вверх
• Повторяет форму корня, но опущен на 1
• Область определения: $x \geq 3$