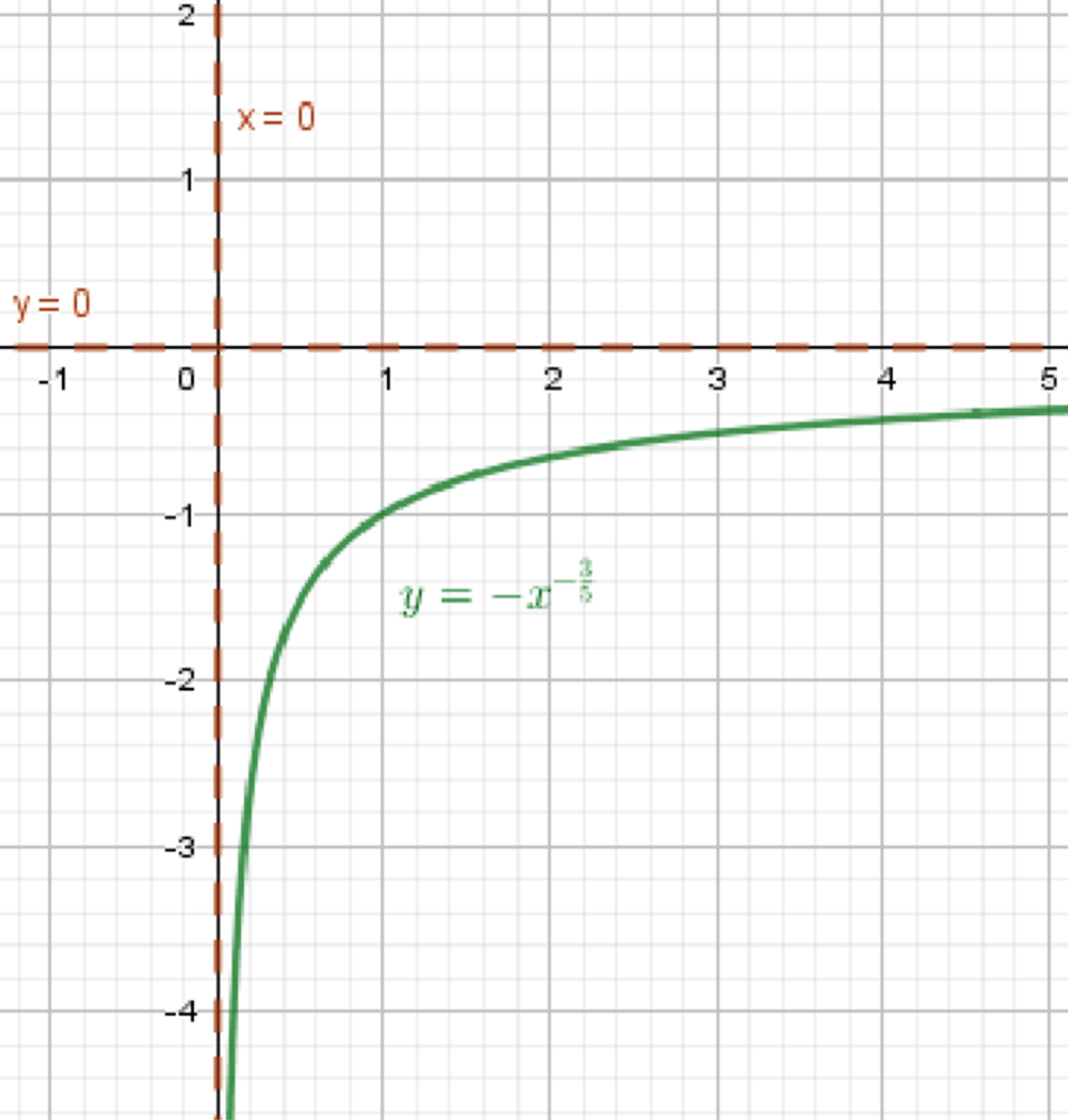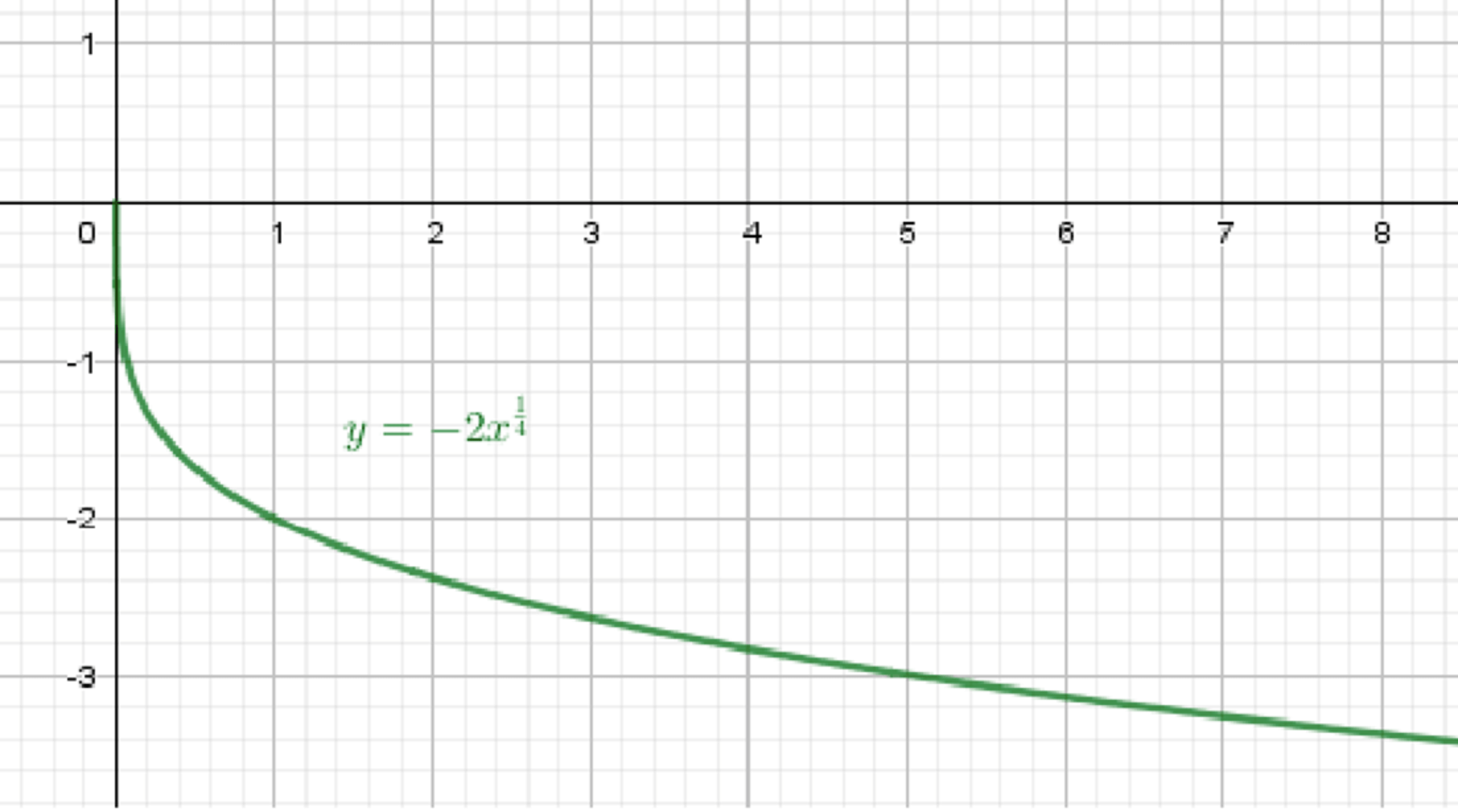ГДЗ 10-11 Класс Номер 38.14 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

а) $y = 2x^{\frac{1}{3}}$;

б) $y = -x^{-\frac{3}{5}}$;

в) $y = \frac{1}{2}x^{\frac{3}{2}}$;

г) $y = -2x^{\frac{1}{4}}$

Построить график функции:

а) $y = 2x^{\frac{1}{3}}$;

Построим график функции $y = x^{\frac{1}{3}}$;
Растянем его в два раза от оси абсцисс:

б) $y = -x^{-\frac{3}{5}}$;

Построим график функции $y = x^{-\frac{3}{5}}$;
Отразим его относительно оси абсцисс:

в) $y = \frac{1}{2}x^{\frac{3}{2}}$;

Построим график функции $y = x^{\frac{3}{2}}$;
Сожмем его в два раза к оси абсцисс:

г) $y = -2x^{\frac{1}{4}}$;

Построим график функции $y = x^{\frac{1}{4}}$;
Отразим его относительно оси абсцисс;
Растянем его в два раза от оси абсцисс:

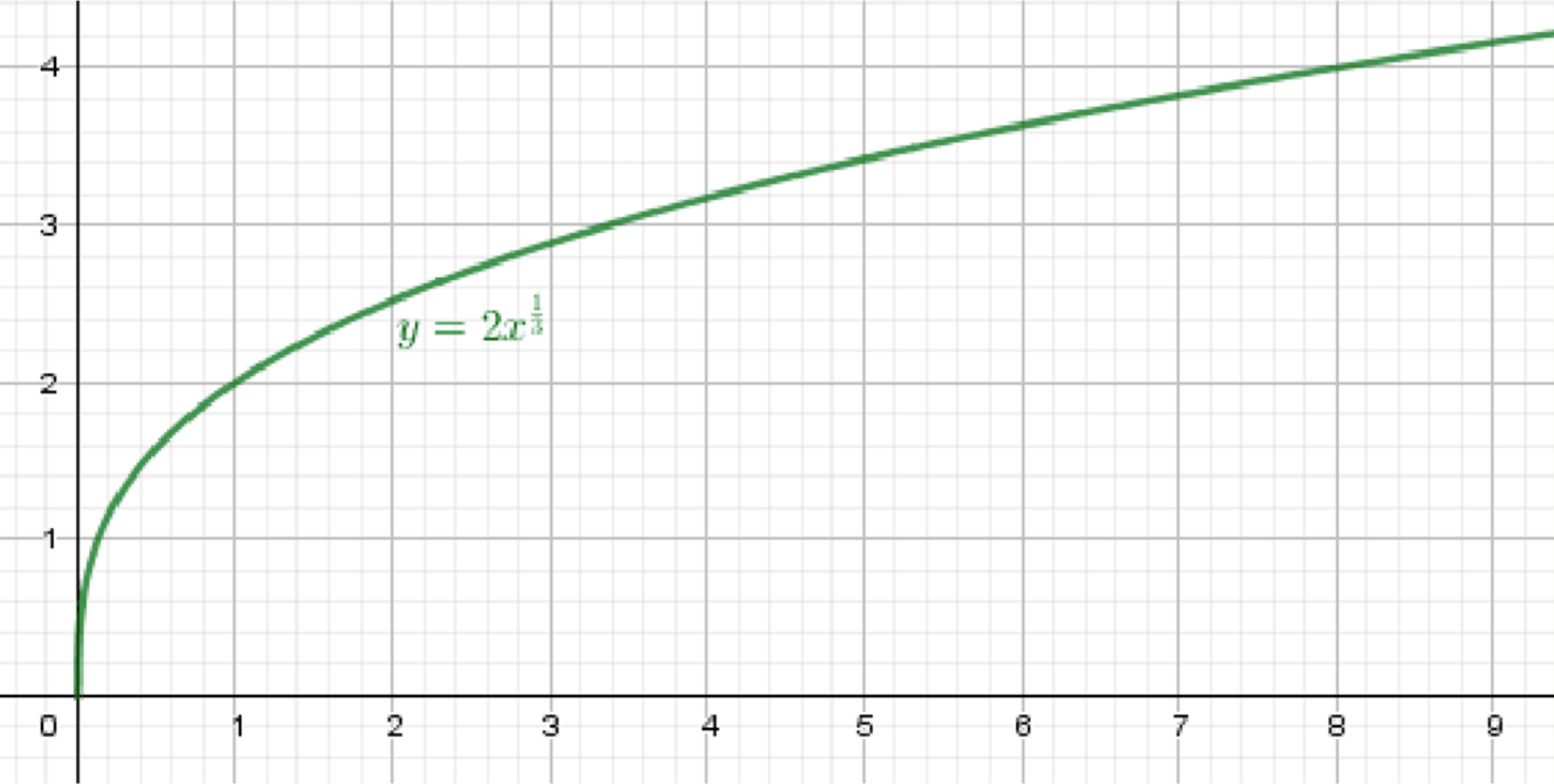
а) $y = 2x^{\frac{1}{3}}$

Шаг 1: Базовая функция

Функция $y = x^{\frac{1}{3}}$ — это кубический корень.

• Область определения: $x \in \mathbb{R}$
• Чётная степень знаменателя (3) и нечётная степень числителя (1) → функция определена для всех $x$
• Функция нечётная: симметрична относительно начала координат
• Примеры точек:
  • $x = -8 \Rightarrow y = -2$
  • $x = -1 \Rightarrow y = -1$
  • $x = 0 \Rightarrow y = 0$
  • $x = 1 \Rightarrow y = 1$
  • $x = 8 \Rightarrow y = 2$

Шаг 2: Умножение на 2

Функция становится:

$$y = 2x^{\frac{1}{3}}$$

• Это растягивает график в 2 раза от оси абсцисс (ось $x$)
• Все значения $y$ удваиваются при тех же $x$

Итоговое описание

• Область определения: вся числовая прямая
• Точки:
  • $x = 1 \Rightarrow y = 2$
  • $x = -1 \Rightarrow y = -2$
  • $x = 8 \Rightarrow y = 4$
• График симметричен относительно начала координат, растёт медленно

б) $y = -x^{-\frac{3}{5}}$

Шаг 1: Базовая функция

Функция $y = x^{-\frac{3}{5}}$

• Это степень с отрицательной дробью
• $x^{-\frac{3}{5}} = \frac{1}{x^{3/5}} = \frac{1}{\sqrt[5]{x^3}}$
• Область определения: $x > 0$
• Функция убывает, значения положительные
• Примеры точек:
  • $x = 1 \Rightarrow y = 1$
  • $x = 8 \Rightarrow y = \frac{1}{4}$
  • $x \to 0^+ \Rightarrow y \to +\infty$

Шаг 2: Умножение на (–1)

Функция становится:

$$y = -x^{-\frac{3}{5}}$$

• Отражение относительно оси абсцисс (оси $x$)
• Все значения становятся отрицательными, но по модулю те же

Итоговое описание

• Область определения: $x > 0$
• Поведение:
  • При $x \to 0^+ \Rightarrow y \to -\infty$
  • При $x \to +\infty \Rightarrow y \to 0^-$
• Убывающая, вогнутая вниз ветвь под осью $x$

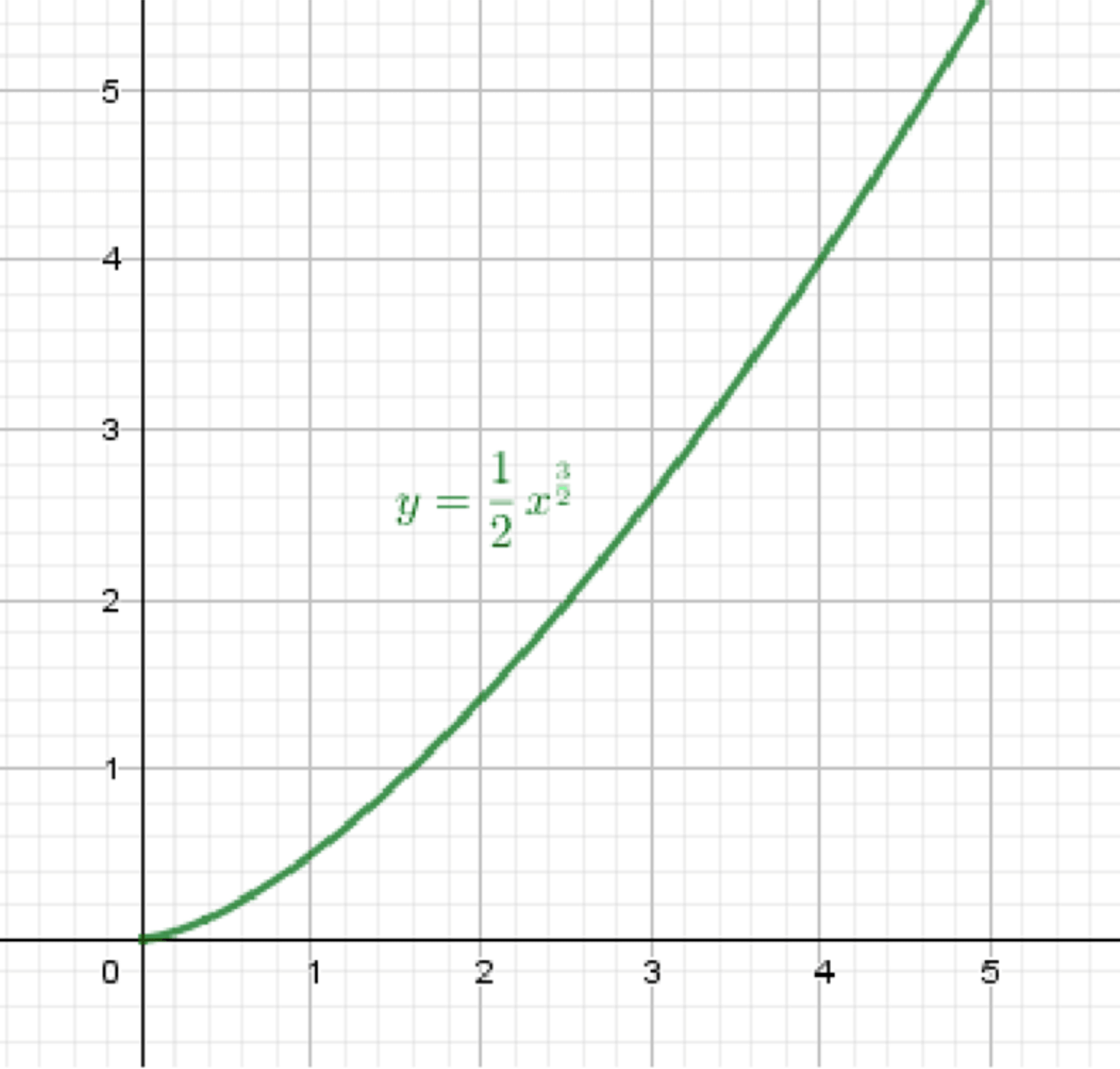
в) $y = \frac{1}{2}x^{\frac{3}{2}}$

Шаг 1: Базовая функция

Функция $y = x^{\frac{3}{2}}$

• $x^{\frac{3}{2}} = (\sqrt{x})^3$
• Область определения: $x \geq 0$
• Монотонно возрастает
• Примеры точек:
  • $x = 0 \Rightarrow y = 0$
  • $x = 1 \Rightarrow y = 1$
  • $x = 4 \Rightarrow y = 8$
  • $x = 9 \Rightarrow y = 27$

Шаг 2: Умножение на $\frac{1}{2}$

Функция становится:

$$y = \frac{1}{2}x^{\frac{3}{2}}$$

• Это сжатие графика к оси абсцисс (ось $x$)
• Все значения $y$ становятся в 2 раза меньше

Итоговое описание

• Область определения: $x \geq 0$
• Кривая возрастает, как и прежде, но медленнее:
  • $x = 1 \Rightarrow y = \frac{1}{2}$
  • $x = 4 \Rightarrow y = 4$
  • $x = 9 \Rightarrow y = 13.5$

г) $y = -2x^{\frac{1}{4}}$

Шаг 1: Базовая функция

Функция $y = x^{\frac{1}{4}}$

• Это корень четвёртой степени: $\sqrt[4]{x}$
• Область определения: $x \geq 0$
• Очень медленно растущая функция
• Примеры точек:
  • $x = 0 \Rightarrow y = 0$
  • $x = 1 \Rightarrow y = 1$
  • $x = 16 \Rightarrow y = 2$

Шаг 2: Умножение на (–1) и на 2

Функция становится:

$$y = -2x^{\frac{1}{4}}$$

• Сначала отражаем относительно оси абсцисс
• Затем растягиваем в 2 раза вниз
• Все значения становятся отрицательными и увеличиваются по модулю в 2 раза

Итоговое описание

• Область определения: $x \geq 0$
• Кривая идёт вниз от начала координат:
  • $x = 0 \Rightarrow y = 0$
  • $x = 1 \Rightarrow y = -2$
  • $x = 16 \Rightarrow y = -4$
• Монотонно убывает вниз (по значениям $y$, хотя $x$ растёт)