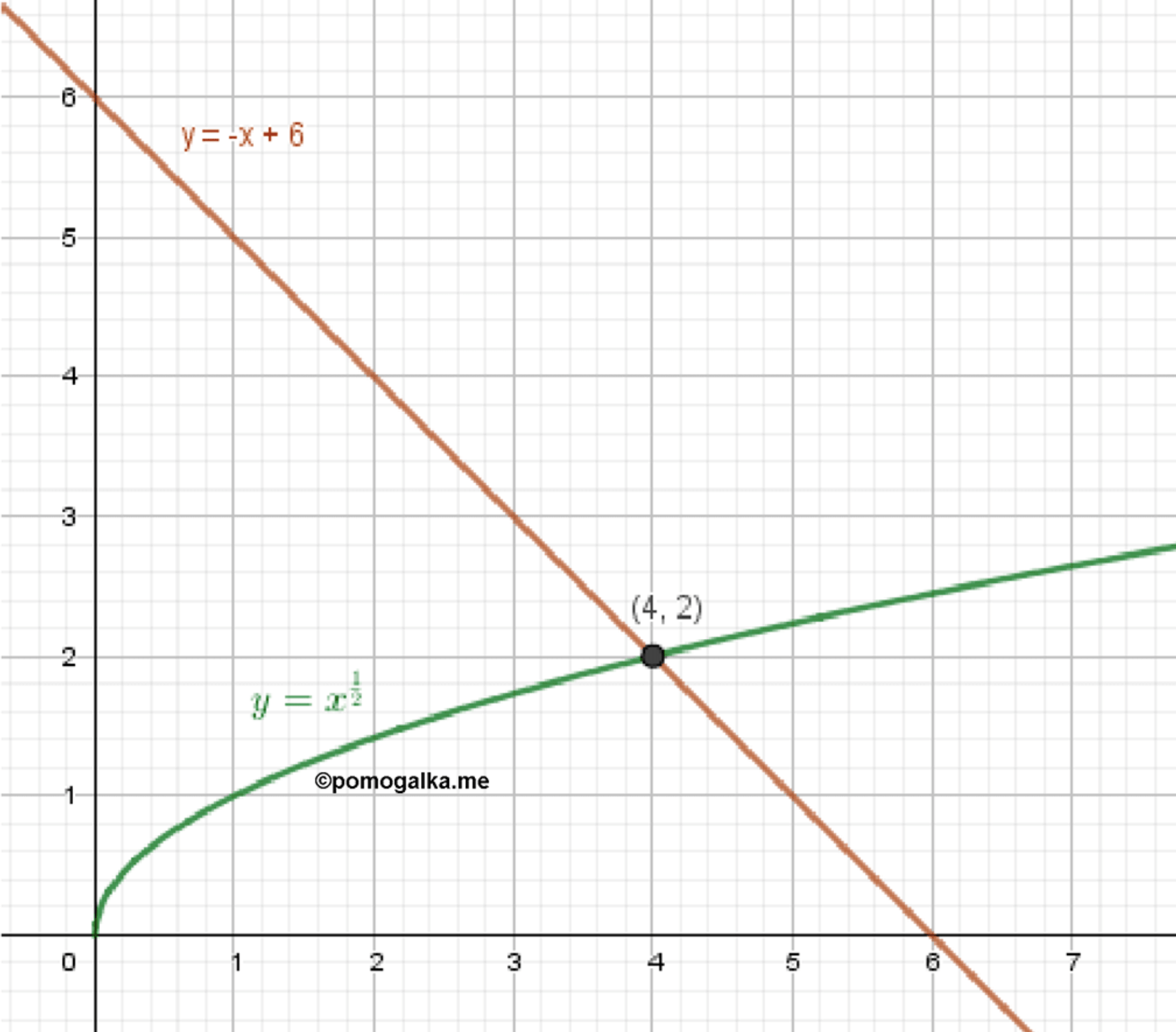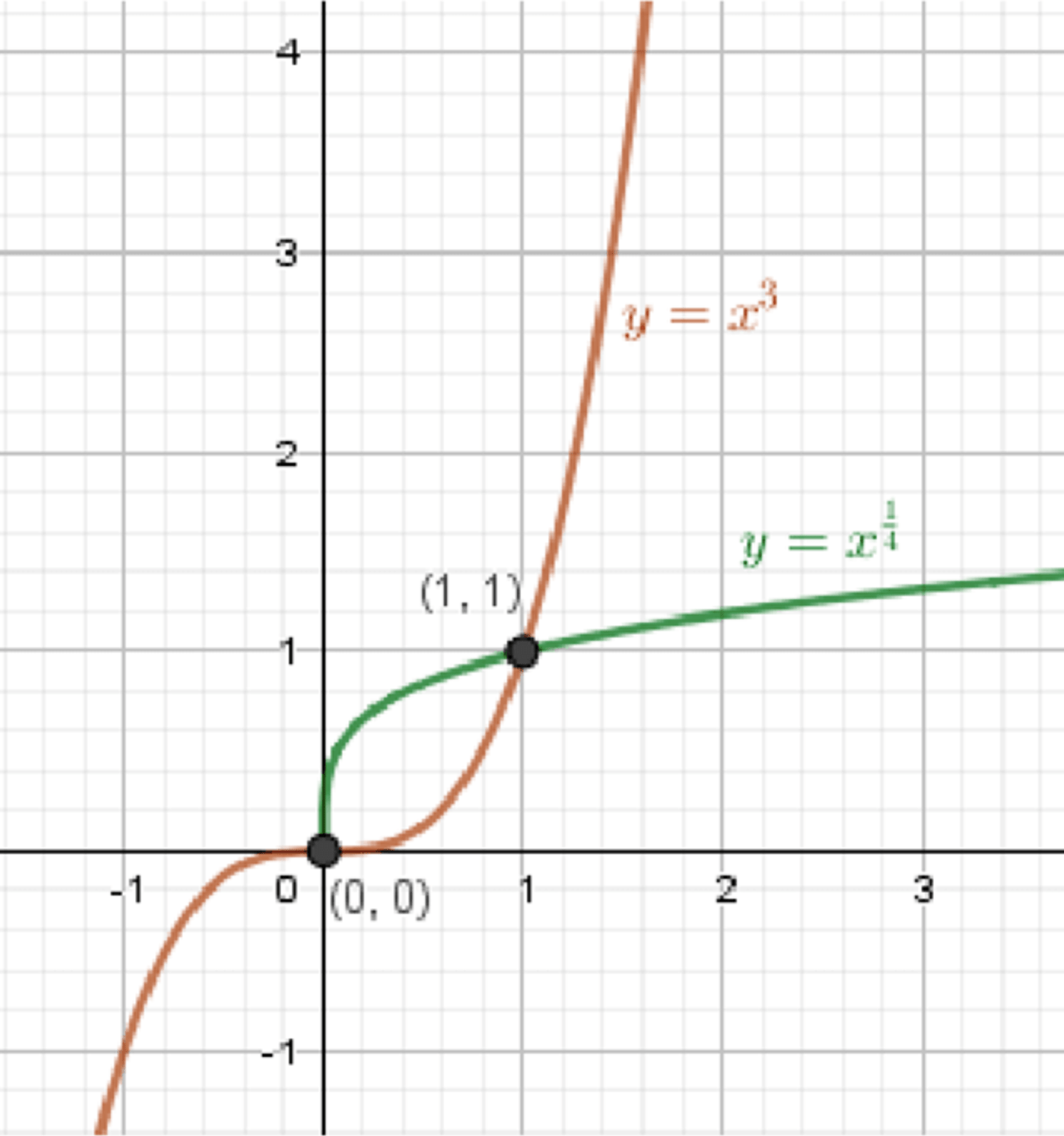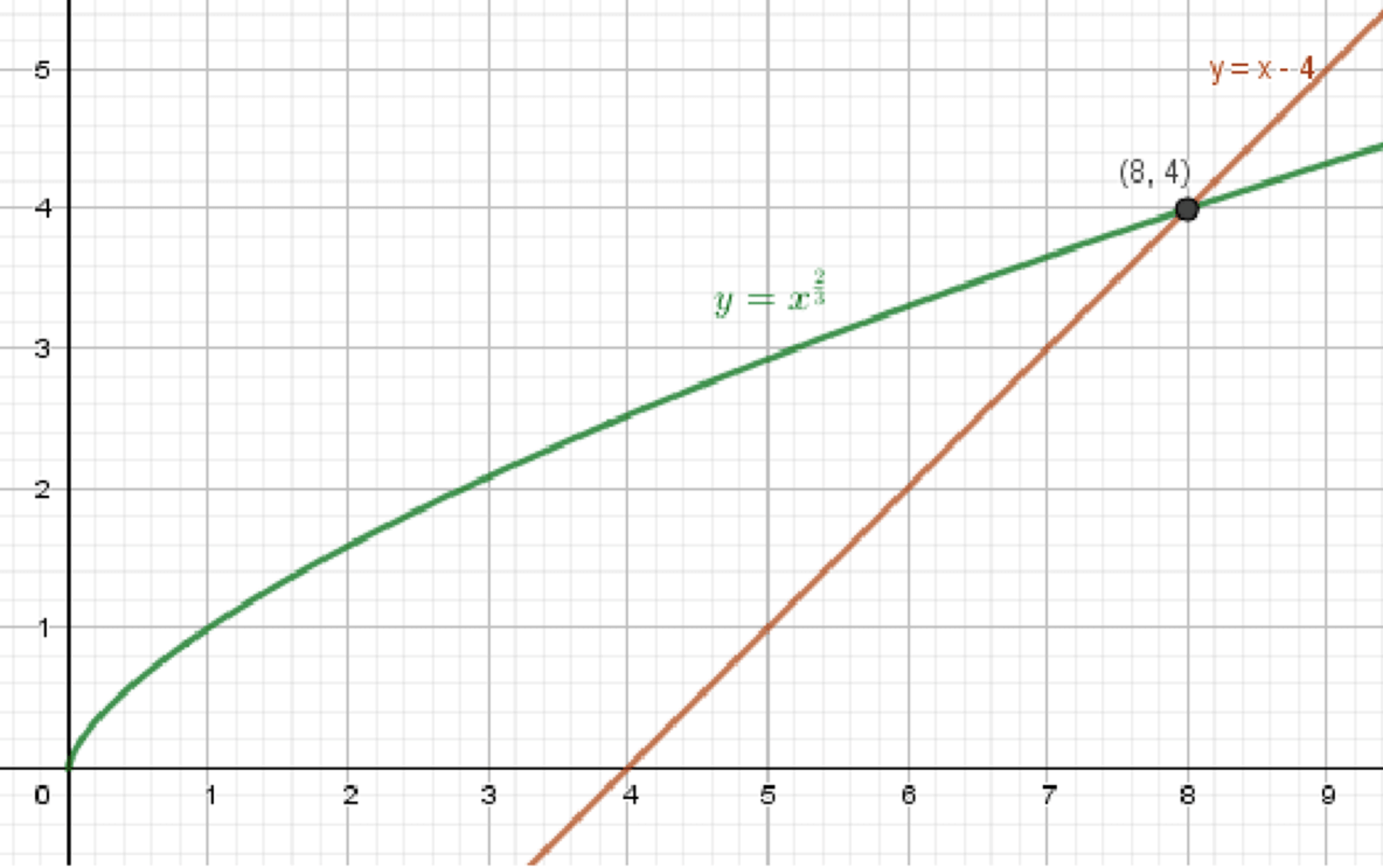ГДЗ 10-11 Класс Номер 38.15 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Решите графически уравнение:

а) $x^{\frac{1}{2}} = 6 — x$;

б) $x^{\frac{3}{2}} = \frac{1}{x^2}$;

в) $x^{\frac{1}{4}} = x^3$;

г) $x^{\frac{2}{3}} = x — 4$

Решить графически уравнение:

а) $x^{\frac{1}{2}} = 6 — x$;
$y = x^{\frac{1}{2}}$ — степенная функция:

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 4 \\ \hline y & 0 & 1 & 2 \\ \hline \end{array}$$

$y = 6 — x$ — уравнение прямой:

$$\begin{array}{|c|c|c|} \hline x & 2 & 4 \\ \hline y & 4 & 2 \\ \hline \end{array}$$

Графики функций:

Ответ: $x = 4$.

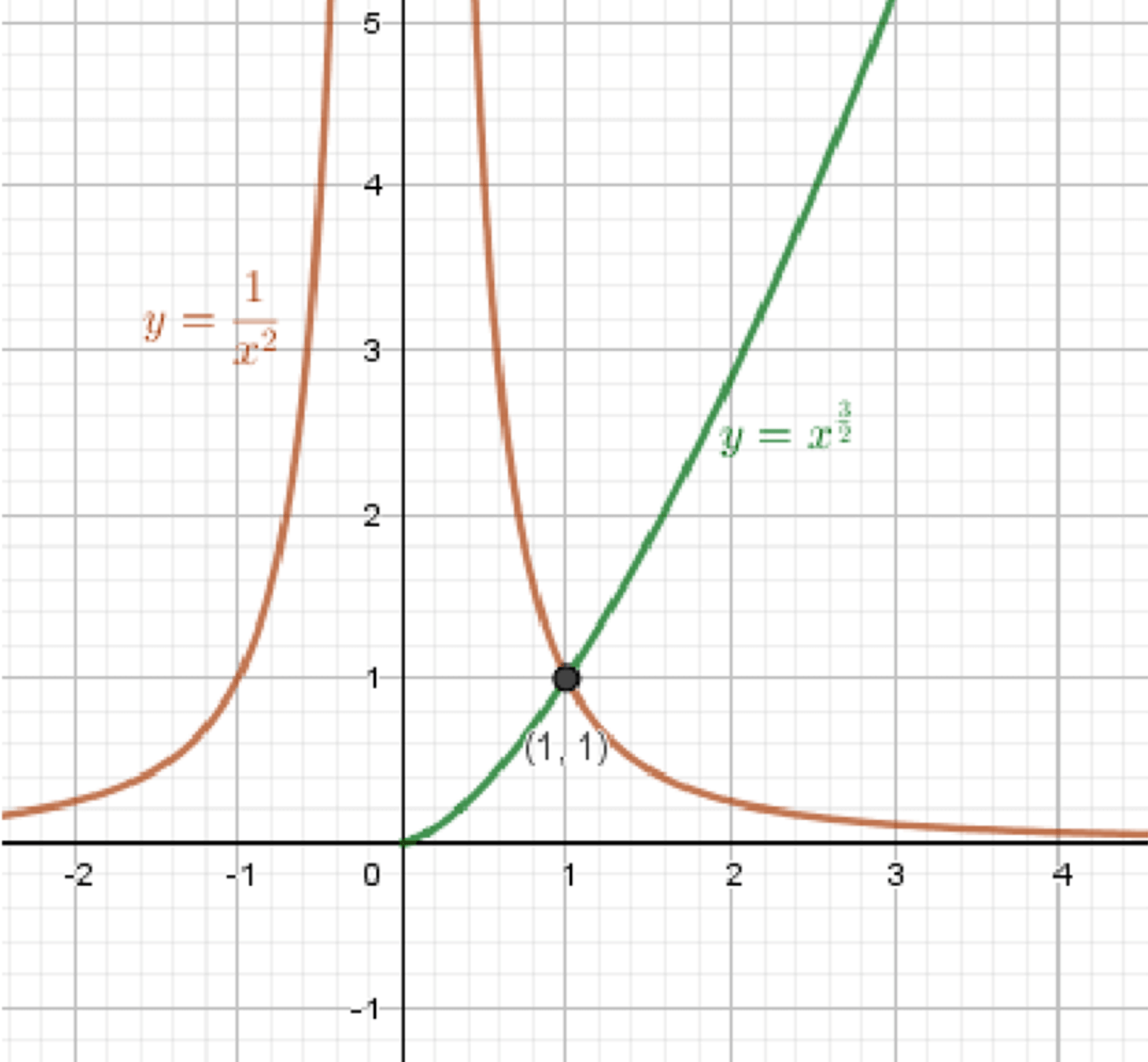
б) $x^{\frac{3}{2}} = \frac{1}{x^2}$;
$y = x^{\frac{3}{2}}$ — степенная функция:

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 4 \\ \hline y & 0 & 1 & 8 \\ \hline \end{array}$$

$y = \frac{1}{x^2} = x^{-2}$ — степенная функция:

$$\begin{array}{|c|c|c|c|} \hline x & 0{,}5 & 1 & 2 \\ \hline y & 4 & 1 & 0{,}25 \\ \hline \end{array}$$

Графики функций:

Ответ: $x = 1$.

в) $x^{\frac{1}{4}} = x^3$;
$y = x^{\frac{1}{4}}$ — степенная функция:

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 16 \\ \hline y & 0 & 1 & 2 \\ \hline \end{array}$$

$y = x^3$ — степенная функция:

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 2 \\ \hline y & 0 & 1 & 8 \\ \hline \end{array}$$

Графики функций:

Ответ: $x_1 = 0$; $x_2 = 1$.

г) $x^{\frac{2}{3}} = x — 4$;
$y = x^{\frac{2}{3}}$ — степенная функция:

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 8 \\ \hline y & 0 & 1 & 4 \\ \hline \end{array}$$

$y = x — 4$ — уравнение прямой:

$$\begin{array}{|c|c|c|} \hline x & 4 & 6 \\ \hline y & 0 & 2 \\ \hline \end{array}$$

Графики функций:

Ответ: $x = 8$.

а) $x^{\frac{1}{2}} = 6 — x$

Шаг 1: Представим уравнение как систему двух графиков

Пусть:

• $y_1 = x^{\frac{1}{2}}$ — степенная функция (корень квадратный)
• $y_2 = 6 — x$ — линейная функция

Найдем точку пересечения графиков:
Это значение $x$, при котором $y_1 = y_2$

Шаг 2: Таблица значений $y_1 = \sqrt{x}$

$$\begin{array}{|c|c|} \hline x & y_1 = \sqrt{x} \\ \hline 0 & 0 \\ 1 & 1 \\ 4 & 2 \\ \hline \end{array}$$

• Область определения: $x \geq 0$
• График — плавная возрастающая кривая от точки $(0; 0)$

Шаг 3: Таблица значений $y_2 = 6 — x$

$$\begin{array}{|c|c|} \hline x & y_2 = 6 — x \\ \hline 2 & 4 \\ 4 & 2 \\ \hline \end{array}$$

• Прямая с угловым коэффициентом $-1$, убывает
• При $x = 4$, $y = 2$

Шаг 4: Анализ пересечения

• В точке $x = 4$:
  $y_1 = \sqrt{4} = 2$,
  $y_2 = 6 — 4 = 2$
  ⇒ графики пересекаются

Ответ: $\boxed{x = 4}$

б) $x^{\frac{3}{2}} = \dfrac{1}{x^2}$

Шаг 1: Перепишем

Пусть:

• $y_1 = x^{\frac{3}{2}}$
• $y_2 = x^{-2} = \dfrac{1}{x^2}$

Шаг 2: Таблица значений $y_1 = x^{\frac{3}{2}}$

$$\begin{array}{|c|c|} \hline x & y_1 = \sqrt{x^3} \\ \hline 0 & 0 \\ 1 & 1 \\ 4 & 8 \\ \hline \end{array}$$

• Область определения: $x \geq 0$
• Резко возрастает

Шаг 3: Таблица значений $y_2 = \dfrac{1}{x^2}$

$$\begin{array}{|c|c|} \hline x & y_2 \\ \hline 0.5 & 4 \\ 1 & 1 \\ 2 & 0.25 \\ \hline \end{array}$$

• Область определения: $x \neq 0$, положительная ветвь: $x > 0$
• Функция убывает

Шаг 4: Пересечение

• При $x = 1$:
  $y_1 = 1^{\frac{3}{2}} = 1$
  $y_2 = \frac{1}{1^2} = 1$ ⇒ совпадают

Ответ: $\boxed{x = 1}$

в) $x^{\frac{1}{4}} = x^3$

Шаг 1: Обозначим

• $y_1 = x^{\frac{1}{4}}$
• $y_2 = x^3$

Шаг 2: Таблица значений $y_1 = x^{\frac{1}{4}}$

$$\begin{array}{|c|c|} \hline x & y_1 \\ \hline 0 & 0 \\ 1 & 1 \\ 16 & 2 \\ \hline \end{array}$$

• Область определения: $x \geq 0$
• Очень медленно растущая функция

Шаг 3: Таблица значений $y_2 = x^3$

$$\begin{array}{|c|c|} \hline x & y_2 \\ \hline 0 & 0 \\ 1 & 1 \\ 2 & 8 \\ \hline \end{array}$$

• Быстро возрастает при $x > 1$

Шаг 4: Анализ пересечений

• При $x = 0 \Rightarrow y_1 = y_2 = 0$
• При $x = 1 \Rightarrow y_1 = y_2 = 1$

Ответ: $\boxed{x_1 = 0;\ x_2 = 1}$

г) $x^{\frac{2}{3}} = x — 4$

Шаг 1: Обозначим

• $y_1 = x^{\frac{2}{3}}$
• $y_2 = x — 4$

Шаг 2: Таблица значений $y_1 = x^{\frac{2}{3}}$

• Степень с чётным числителем → функция определена на всей оси $x$
• Примеры:

$$\begin{array}{|c|c|} \hline x & y_1 \\ \hline 0 & 0 \\ 1 & 1 \\ 8 & 4 \\ \hline \end{array}$$

Шаг 3: Таблица значений $y_2 = x — 4$

$$\begin{array}{|c|c|} \hline x & y_2 \\ \hline 4 & 0 \\ 6 & 2 \\ \hline \end{array}$$

• Прямая с угловым коэффициентом 1, пересекает ось $y$ в точке $(0; -4)$

Шаг 4: Пересечение

• При $x = 8$:
  $y_1 = 8^{2/3} = 4$,
  $y_2 = 8 — 4 = 4$ ⇒ совпадают

Ответ: $\boxed{{\displaystyle x=8}}$