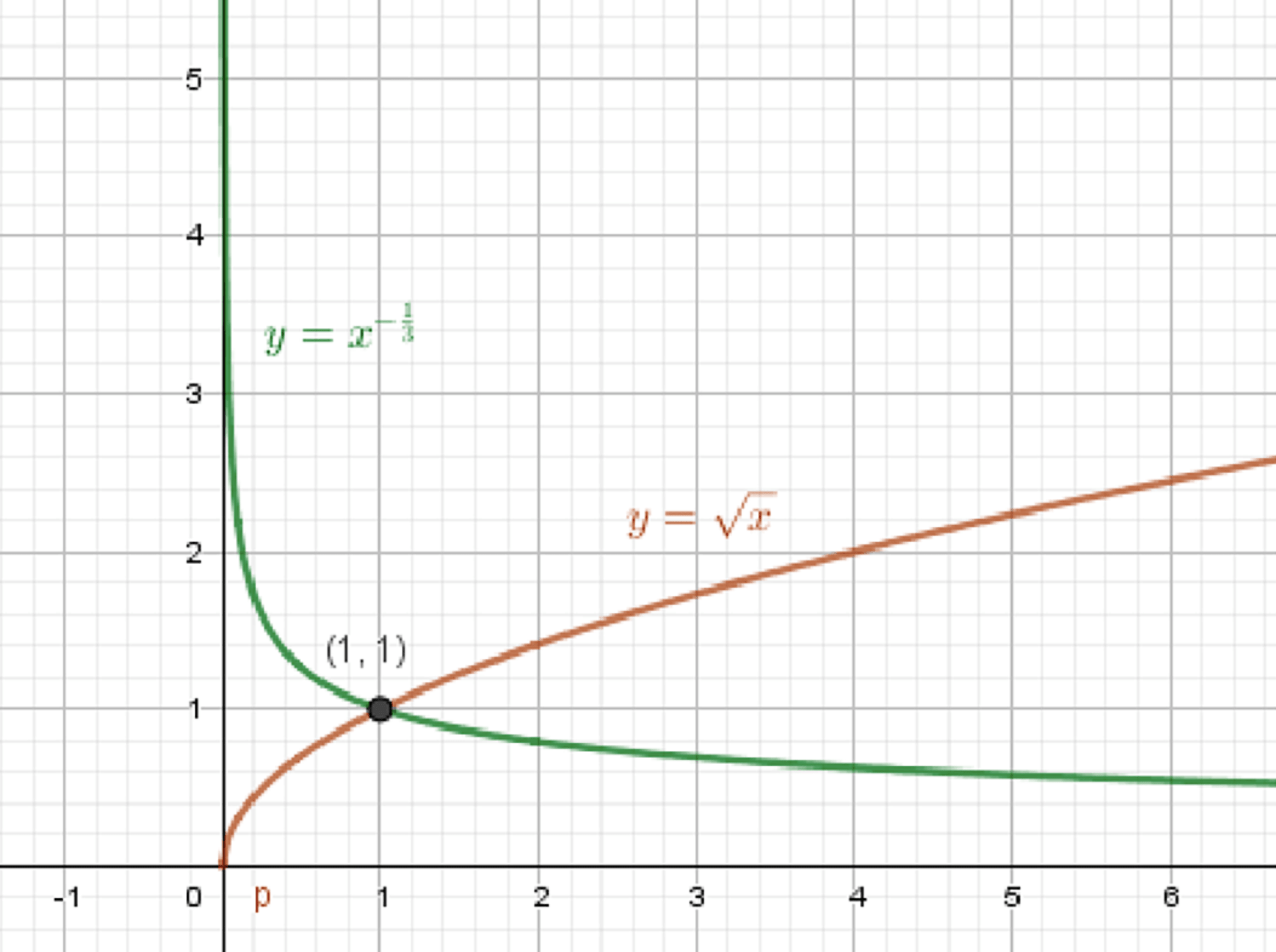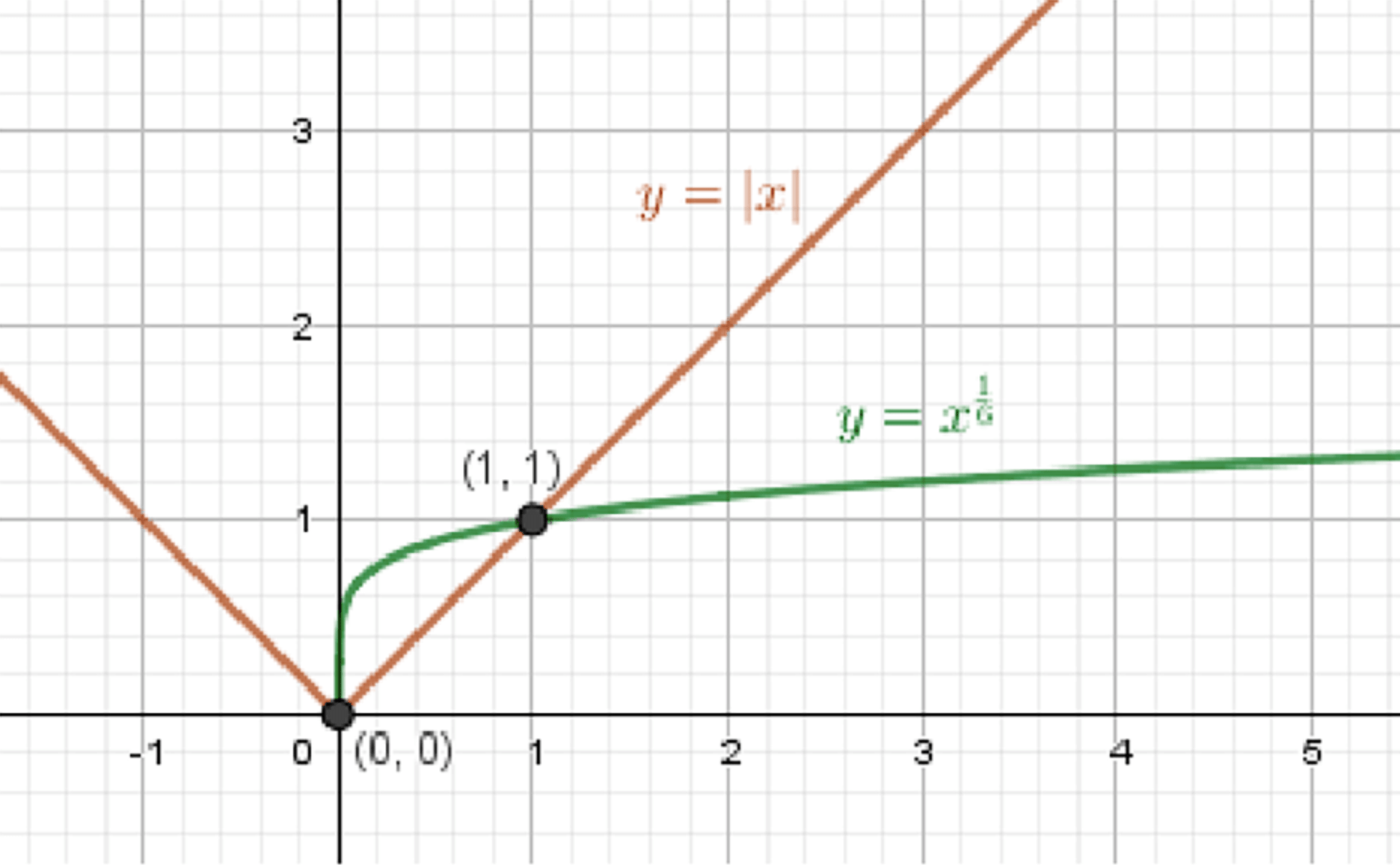ГДЗ 10-11 Класс Номер 38.16 Алгебра И Начала Математического Анализа Мордкович — Подробные Ответы

Решите графически систему уравнений:

а)

$$\{\begin{array}{l}y=x^{\frac{5}{2}},\\ y=1\end{array}$$

б)

$$\{\begin{array}{l}y=x^{-\frac{1}{3}},\\ y=\sqrt{x}\end{array}$$

в)

$$\begin{cases} y = x^{\frac{1}{6}}, \\ y = |x| \end{cases}$$

г)

$$\{\begin{array}{l}y=x^{-\frac{2}{3}},\\ 2x-y-1=0\end{array}$$

Решить графически систему уравнений:

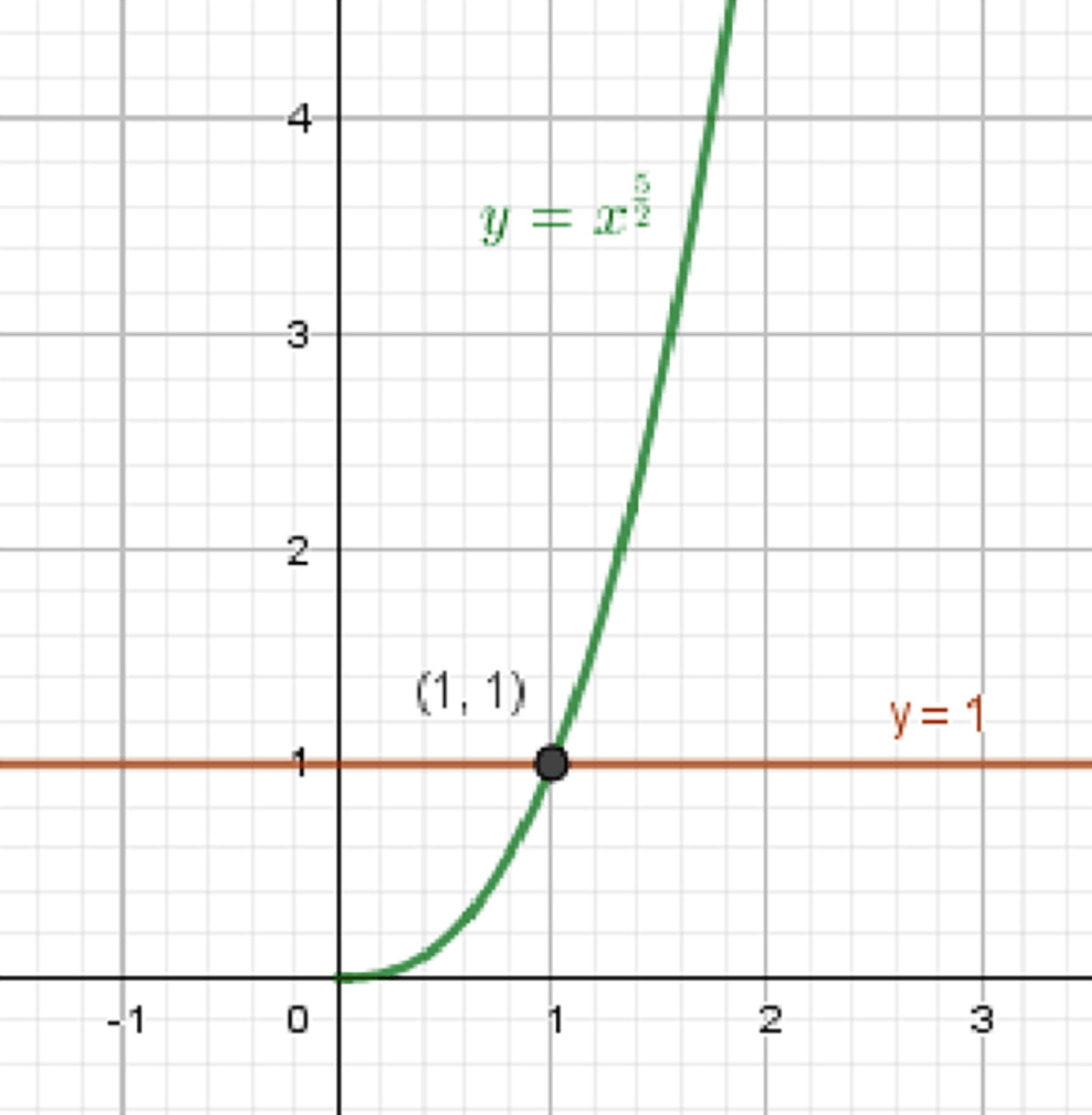
а)

$$\begin{cases} y = x^{\frac{5}{2}}, \\ y = 1 \end{cases}$$

$y = x^{\frac{5}{2}}$ — степенная функция:

Графики функций:

Ответ: (1; 1).

б)

$$\begin{cases} y = x^{-\frac{1}{3}}, \\ y = \sqrt{x} \end{cases}$$

$y = x^{-\frac{1}{3}}$ — степенная функция:

$y = \sqrt{x}$ — уравнение ветви параболы:

Графики функций:

Ответ: (1; 1).

в)

$$\begin{cases} y = x^{\frac{1}{6}}, \\ y = |x| \end{cases}$$

$y = x^{\frac{1}{6}}$ — степенная функция:

$y = |x|$ — уравнение ломаной:

Графики функций:

Ответ: (0; 0); (1; 1).

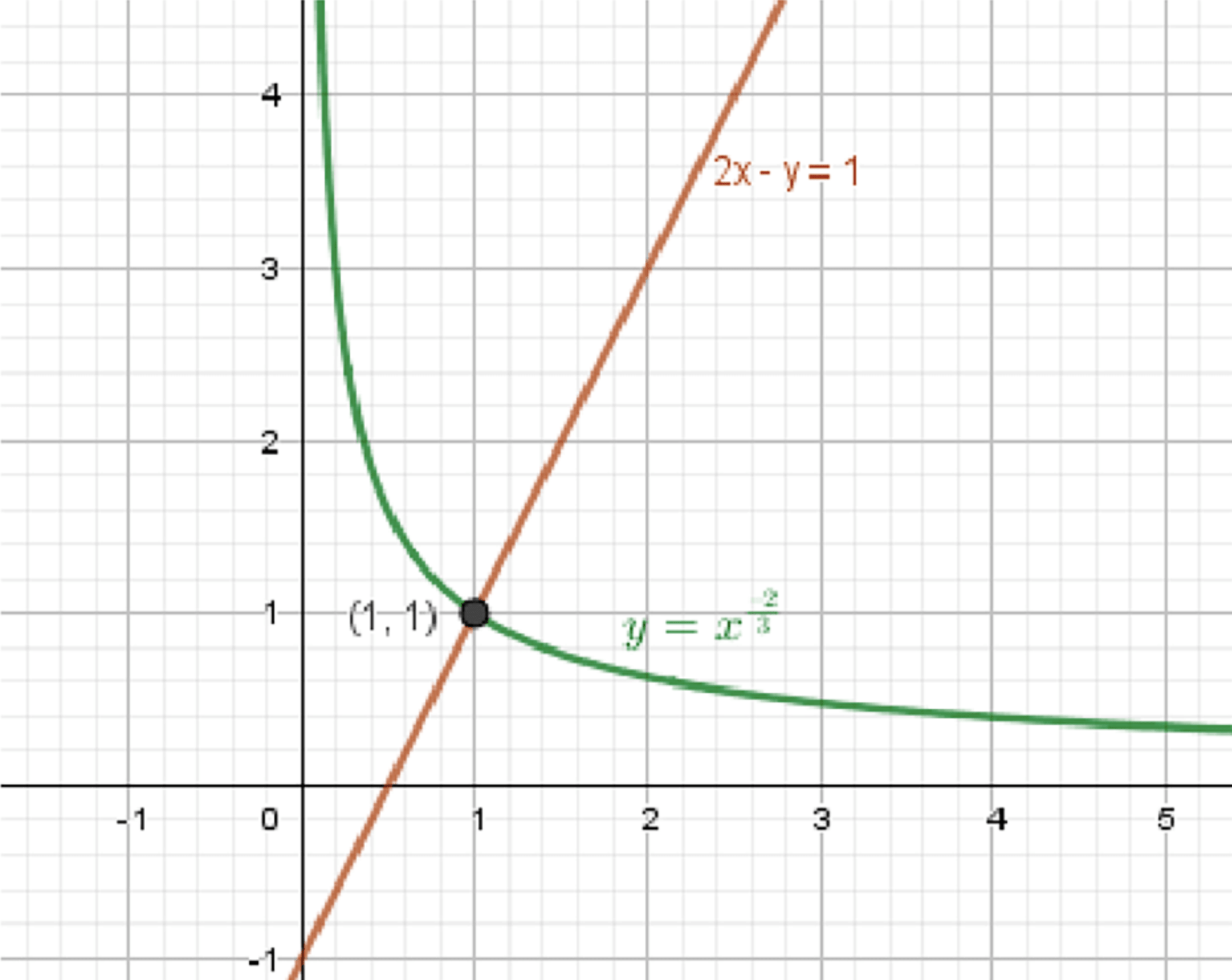
г)

$$\begin{cases} y = x^{-\frac{2}{3}}, \\ 2x — y — 1 = 0 \end{cases}$$

$y = x^{-\frac{2}{3}}$ — степенная функция:

$y = 2x — 1$ — уравнение прямой:

Графики функций:

Ответ: (1; 1).

а)

$$\begin{cases} y = x^{\frac{5}{2}}, \\ y = 1 \end{cases}$$

1. Первая функция: $y = x^{\frac{5}{2}}$

• Это функция вида $y = x^n$, где $n = \frac{5}{2} > 0$
• Область определения: $x \geq 0$
• Функция возрастает, строго положительная при $x > 0$
• Поведение у нуля: $y(0) = 0$
• При увеличении $x$ значения $y$ быстро растут

Таблица значений:

2. Вторая функция: $y = 1$

• Прямая, параллельная оси $x$, проходит через все точки с $y = 1$
• Область определения: $x \in \mathbb{R}$

3. Поиск точки пересечения:

Найдем $x$, при котором графики пересекаются:

$$x^{\frac{5}{2}} = 1 \Rightarrow x = 1$$

Ответ: $\boxed{(1;\ 1)}$

б)

$$\begin{cases} y = x^{-\frac{1}{3}}, \\ y = \sqrt{x} \end{cases}$$

1. Первая функция: $y = x^{-\frac{1}{3}}$

• Форма: отрицательная дробная степень
• $x^{-\frac{1}{3}} = \frac{1}{\sqrt[3]{x}}$
• Область определения: $x > 0$
• Убывает при росте $x$
• Значения положительные

Таблица:

2. Вторая функция: $y = \sqrt{x} = x^{1/2}$

• Область определения: $x \geq 0$
• Возрастает
• Значения положительные

Таблица:

3. Поиск точки пересечения:

Найдем $x$, при котором функции равны:

$$x^{-\frac{1}{3}} = \sqrt{x} \Rightarrow x^{-1/3} = x^{1/2} \Rightarrow x^{-1/3 — 1/2} = 1 \Rightarrow x^{-5/6} = 1 \Rightarrow x = 1$$

Ответ: $\boxed{(1;\ 1)}$

в)

$$\begin{cases} y = x^{\frac{1}{6}}, \\ y = |x| \end{cases}$$

1. Первая функция: $y = x^{1/6}$

• Чётный знаменатель в дроби ⇒ область: $x \geq 0$
• Возрастает очень медленно

Таблица:

2. Вторая функция: $y = |x|$

• График состоит из двух лучей:
  • $y = x$, если $x \geq 0$
  • $y = -x$, если $x < 0$
• Ломаная, симметричная относительно оси $y$

Таблица:

3. Поиск пересечений:

Графики пересекаются в тех точках, где:

$$x^{1/6} = |x|$$

Проверим:

• При $x = 0$: $y = 0$ — совпадают
• При $x = 1$: $y = 1$ — совпадают

Другие значения не подходят, так как:

• Для $x > 1$: $x^{1/6} < x$, значит графики не пересекаются
• Для $x < 0$: $x^{1/6}$ не определён

Ответ: $\boxed{(0;\ 0);\ (1;\ 1)}$

г)

$$\begin{cases} y = x^{-\frac{2}{3}}, \\ 2x — y — 1 = 0 \end{cases}$$

1. Первая функция: $y = x^{-\frac{2}{3}}$

• $x^{-\frac{2}{3}} = \frac{1}{\sqrt[3]{x^2}}$
• Область определения: $x \neq 0$
• График имеет две ветви: при $x > 0$ и $x < 0$
• Функция чётная (т.к. степень чётная), значения положительные

Таблица:

2. Вторая функция: $2x — y — 1 = 0 \Rightarrow y = 2x — 1$

• Прямая с угловым коэффициентом 2 и сдвигом на -1 по оси $y$

Таблица:

3. Поиск пересечений:

Ищем $x$, при котором:

$$x^{-\frac{2}{3}} = 2x — 1$$

Проверка при $x = 1$:

• Левая часть: $1^{-\frac{2}{3}} = 1$
• Правая часть: $2(1) — 1 = 1$

⇒ Совпадают

Других решений нет:

• При $x > 1$, $x^{-\frac{2}{3}}$ убывает, а $2x — 1$ возрастает
• При $x < 1$, функция $2x — 1$ убывает, а $x^{-\frac{2}{3}}$ растёт, но значения разные

Ответ: $\boxed{{\displaystyle (1;1)}}$